Chào mừng các em học sinh đến với bài giải chi tiết phần A. Tái hiện, củng cố trang 31 trong sách Bài tập phát triển năng lực Toán 4 tập 2. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp những bài giải chính xác, dễ hiểu và phù hợp với chương trình học.
Trong một lớp có 22 bạn trai và 18 bạn gái. a) Viết tỉ số của số bạn trai và số bạn gái. Tổng hai số là 256. Tỉ số của hai số đó là ....
Trong một lớp có 22 bạn trai và 18 bạn gái.
a) Viết tỉ số của số bạn trai và số bạn gái.
b) Viết tỉ số của số bạn gái và số bạn trai.
c) Viết tỉ số của số bạn trai và số bạn của cả lớp.
d) Viết tỉ số của số bạn gái và số bạn của cả lớp.
Phương pháp giải:
Tỉ số của a và b là a : b hay $\frac{a}{b}$ (b khác 0).
Lời giải chi tiết:
Ta có: tổng số bạn trai và bạn gái trong một lớp là: 22 + 18 = 40 (bạn)
a) Tỉ số của số bạn trai và số bạn gái là 22 : 18 hay $\frac{{22}}{{18}}$
b) Tỉ số của số bạn gái và số bạn trai là 18 : 22 hay $\frac{{18}}{{22}}$
c) Tỉ số của số bạn trai và số bạn của cả lớp là 22 : 40 hay $\frac{{22}}{{40}}$
d) Tỉ số của số bạn gái và số bạn của cả lớp là 18 : 40 hay $\frac{{18}}{{40}}$
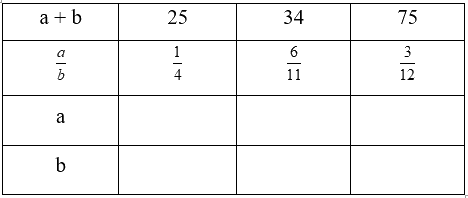
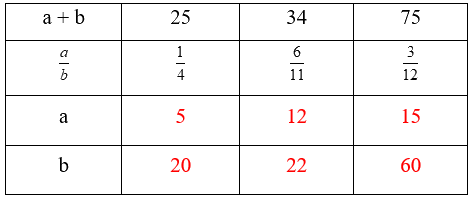
Viết số thích hợp vào ô trống:
Phương pháp giải:
1. Tìm tổng số phần bằng nhau và tìm giá trị của 1 phần.
2. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
3. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).
Lời giải chi tiết:
+) Cột thứ nhất:
Coi số bé gồm 1 phần thì số lớn gồm 4 phần như thế.
Tổng số phần bằng nhau là: 1 + 4 = 5 (phần)
Số bé là: 25 : 5 × 1 = 5
Số lớn là: 25 – 5 = 20
+) Cột thứ hai:
Coi số bé gồm 6 phần thì số lớn gồm 11 phần như thế.
Tổng số phần bằng nhau là: 6 + 11 = 17 (phần)
Số bé là: 34 : 17 × 6 = 12
Số lớn là: 34 – 12 = 22
+) Cột thứ ba:
Coi số bé gồm 3 phần bằng nhau thì số lớn gồm 12 phần như thế.
Tổng số phần bằng nhau là: 3 + 12 = 15 (phần)
Số bé là: 75 : 15 × 3 = 15
Số lớn là: 75 – 15 = 60
Ta có bảng kết quả như sau:
Tổng của hai số là 256. Tỉ số của hai số đó là $\frac{1}{3}$. Tìm hai số đó.
Phương pháp giải:
1. Vẽ sơ đồ
2. Tìm tổng số phần bằng nhau và giá trị của 1 phần.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).
Lời giải chi tiết:
Ta có sơ đồ:
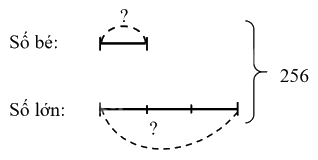
Theo sơ đồ, tổng số phần bằng nhau là:
1 + 3 = 4 (phần)
Số bé là: 256 : 4 × 1 = 64
Số lớn là: 256 – 64 = 192
Đáp số: Số lớn: 192; Số bé: 64.
Điền vào chỗ trống cho thích hợp:
a) Tứ giác ABCD có:

Cạnh AB ............... với cạnh CD.
Cạnh BC ............... với cạnh AD.
AB ............... CD, BC ............... AD.
Tứ giác ABCD có 4 góc ...............
Tứ giác ABCD là hình ...............
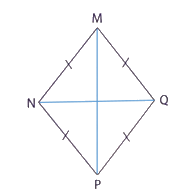
b) Tứ giác MNPQ có:
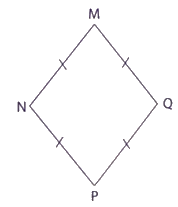
Cạnh MN ............... với cạnh QP.
Cạnh MQ ............... với cạnh NP.
MN ............... NP ............... PQ ............... MQ.
Tứ giác MNPQ là hình ...............
c) Vẽ hai đường chéo của tứ giác MNPQ.
Đường chéo MP ............... NQ
Phương pháp giải:
Quan sát hình vẽ và dùng thước đo độ dài các cạnh rồi điền vào chỗ chấm.
Lời giải chi tiết:
a) Tứ giác ABCD có:
Cạnh AB song song với cạnh CD.
Cạnh BC song song với cạnh AD.
AB = CD, BC = AD.
Tứ giác ABCD có 4 góc vuông
Tứ giác ABCD là hình chữ nhật
b) Tứ giác MNPQ có:
Cạnh MN song song với cạnh QP.
Cạnh MQ song song với cạnh NP.
MN = NP = PQ = MQ.
Tứ giác MNPQ là hình thoi
c) Vẽ hai đường chéo của tứ giác MNPQ.
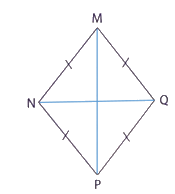
Đường chéo MP vuông góc với NQ
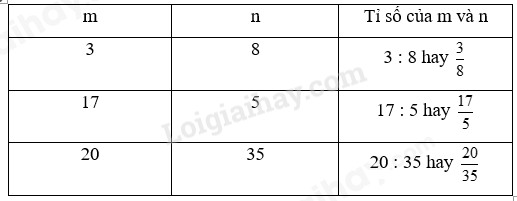
Viết tỉ số vào ô trống cho thích hợp:
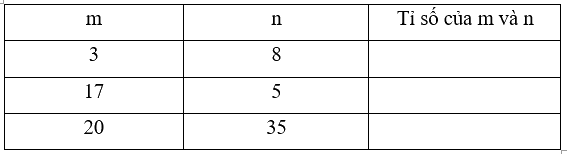
Phương pháp giải:
Tỉ số của m và n là m : n hay $\frac{m}{n}$ (với n khác 0)
Lời giải chi tiết:

Trong một lớp có 22 bạn trai và 18 bạn gái.
a) Viết tỉ số của số bạn trai và số bạn gái.
b) Viết tỉ số của số bạn gái và số bạn trai.
c) Viết tỉ số của số bạn trai và số bạn của cả lớp.
d) Viết tỉ số của số bạn gái và số bạn của cả lớp.
Phương pháp giải:
Tỉ số của a và b là a : b hay $\frac{a}{b}$ (b khác 0).
Lời giải chi tiết:
Ta có: tổng số bạn trai và bạn gái trong một lớp là: 22 + 18 = 40 (bạn)
a) Tỉ số của số bạn trai và số bạn gái là 22 : 18 hay $\frac{{22}}{{18}}$
b) Tỉ số của số bạn gái và số bạn trai là 18 : 22 hay $\frac{{18}}{{22}}$
c) Tỉ số của số bạn trai và số bạn của cả lớp là 22 : 40 hay $\frac{{22}}{{40}}$
d) Tỉ số của số bạn gái và số bạn của cả lớp là 18 : 40 hay $\frac{{18}}{{40}}$
Tổng của hai số là 256. Tỉ số của hai số đó là $\frac{1}{3}$. Tìm hai số đó.
Phương pháp giải:
1. Vẽ sơ đồ
2. Tìm tổng số phần bằng nhau và giá trị của 1 phần.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).
Lời giải chi tiết:
Ta có sơ đồ:
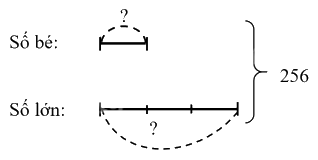
Theo sơ đồ, tổng số phần bằng nhau là:
1 + 3 = 4 (phần)
Số bé là: 256 : 4 × 1 = 64
Số lớn là: 256 – 64 = 192
Đáp số: Số lớn: 192; Số bé: 64.
Viết số thích hợp vào ô trống:
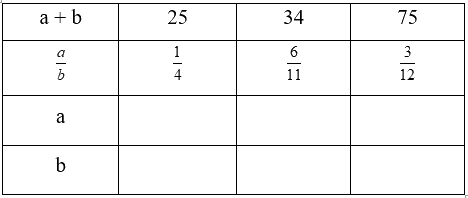
Phương pháp giải:
1. Tìm tổng số phần bằng nhau và tìm giá trị của 1 phần.
2. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
3. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).
Lời giải chi tiết:
+) Cột thứ nhất:
Coi số bé gồm 1 phần thì số lớn gồm 4 phần như thế.
Tổng số phần bằng nhau là: 1 + 4 = 5 (phần)
Số bé là: 25 : 5 × 1 = 5
Số lớn là: 25 – 5 = 20
+) Cột thứ hai:
Coi số bé gồm 6 phần thì số lớn gồm 11 phần như thế.
Tổng số phần bằng nhau là: 6 + 11 = 17 (phần)
Số bé là: 34 : 17 × 6 = 12
Số lớn là: 34 – 12 = 22
+) Cột thứ ba:
Coi số bé gồm 3 phần bằng nhau thì số lớn gồm 12 phần như thế.
Tổng số phần bằng nhau là: 3 + 12 = 15 (phần)
Số bé là: 75 : 15 × 3 = 15
Số lớn là: 75 – 15 = 60
Ta có bảng kết quả như sau:
Viết tỉ số vào ô trống cho thích hợp:
Phương pháp giải:
Tỉ số của m và n là m : n hay $\frac{m}{n}$ (với n khác 0)
Lời giải chi tiết:
Điền vào chỗ trống cho thích hợp:
a) Tứ giác ABCD có:

Cạnh AB ............... với cạnh CD.
Cạnh BC ............... với cạnh AD.
AB ............... CD, BC ............... AD.
Tứ giác ABCD có 4 góc ...............
Tứ giác ABCD là hình ...............
b) Tứ giác MNPQ có:
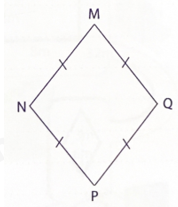
Cạnh MN ............... với cạnh QP.
Cạnh MQ ............... với cạnh NP.
MN ............... NP ............... PQ ............... MQ.
Tứ giác MNPQ là hình ...............
c) Vẽ hai đường chéo của tứ giác MNPQ.
Đường chéo MP ............... NQ
Phương pháp giải:
Quan sát hình vẽ và dùng thước đo độ dài các cạnh rồi điền vào chỗ chấm.
Lời giải chi tiết:
a) Tứ giác ABCD có:
Cạnh AB song song với cạnh CD.
Cạnh BC song song với cạnh AD.
AB = CD, BC = AD.
Tứ giác ABCD có 4 góc vuông
Tứ giác ABCD là hình chữ nhật
b) Tứ giác MNPQ có:
Cạnh MN song song với cạnh QP.
Cạnh MQ song song với cạnh NP.
MN = NP = PQ = MQ.
Tứ giác MNPQ là hình thoi
c) Vẽ hai đường chéo của tứ giác MNPQ.
Đường chéo MP vuông góc với NQ
Phần A. Tái hiện, củng cố trang 31 trong Bài tập phát triển năng lực Toán 4 tập 2 tập trung vào việc giúp học sinh ôn lại kiến thức đã học về các phép tính với số tự nhiên, đặc biệt là phép cộng, trừ, nhân, chia và các bài toán có liên quan đến đơn vị đo độ dài, khối lượng, thời gian. Các bài tập trong phần này thường được trình bày dưới dạng các bài toán thực tế, đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết các tình huống cụ thể.
Phần A bao gồm một số bài tập nhỏ, mỗi bài tập tập trung vào một khía cạnh khác nhau của kiến thức đã học. Dưới đây là nội dung chi tiết của từng bài tập:
Để giải các bài tập trong phần A một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về các phép tính với số tự nhiên, đơn vị đo độ dài, khối lượng, thời gian và các công thức tính toán liên quan. Ngoài ra, học sinh cũng cần phải rèn luyện kỹ năng phân tích đề bài, lựa chọn phương pháp giải phù hợp và kiểm tra lại kết quả sau khi giải xong.
Dưới đây là một số phương pháp giải các bài tập trong phần A:
Bài tập: Một cửa hàng có 35 kg gạo tẻ và 28 kg gạo nếp. Hỏi cửa hàng có tất cả bao nhiêu ki-lô-gam gạo?
Giải:
Số ki-lô-gam gạo cửa hàng có tất cả là:
35 + 28 = 63 (kg)
Đáp số: 63 kg
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tự giải thêm các bài tập tương tự trong sách Bài tập phát triển năng lực Toán 4 tập 2 hoặc tìm kiếm trên các trang web học toán online.
Học toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Các em hãy dành thời gian ôn lại kiến thức đã học, làm bài tập đầy đủ và tìm kiếm sự giúp đỡ của thầy cô giáo hoặc bạn bè khi gặp khó khăn. Chúc các em học tốt môn Toán!
| Phép tính | Kết quả |
|---|---|
| 12 + 23 | 35 |
| 45 - 18 | 27 |
| 6 x 7 | 42 |
| 36 : 4 | 9 |
| Bảng ví dụ các phép tính cơ bản | |