Chào mừng các em học sinh đến với bài giải chi tiết phần C. Vận dụng, phát triển trang 17 trong sách Bài tập phát triển năng lực Toán 4 tập 2. Bài viết này được thiết kế để giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải toán, đồng thời rèn luyện kỹ năng giải quyết vấn đề.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em tự tin hơn trong quá trình học tập và làm bài tập.
Cách đây khoảng 4000 năm, người Ai Cập đã hiểu được phân số và biết các phép tính về phân số. Tuy nhiên, người Ai Cập cổ chỉ thừa nhận ....
Cách đây khoảng 4000 năm, người Ai Cập đã hiểu được phân số và biết các phép tính về phân số. Tuy nhiên, người Ai Cập cổ chỉ thừa nhận các phân số có tử số là 1. Vì vậy, phân số có tử số là 1 còn được gọi là phân số Ai Cập. Phân số \(\frac{5}{6}\) được viết dưới dạng phân số Ai Cập như sau: \(\frac{5}{6} = \frac{1}{2} + \frac{1}{3}\).
Viết phân số \(\frac{7}{{10}}\) dưới dạng tổng các phân số Ai Cập.
Phương pháp giải:
Tách phân số $\frac{7}{{10}}$thành tổng sao cho rút gọn được hai phân số để có tử số là 1.
Lời giải chi tiết:
\(\frac{7}{{10}} = \frac{2}{{10}} + \frac{5}{{10}} = \frac{1}{5} + \frac{1}{2}\)
Viết phân số \(\frac{{11}}{{30}}\) thành tổng hai phân số có tử số là 1 và mẫu số khác nhau.
Phương pháp giải:
Tách tử số của phân số đã cho thành tổng sao cho rút gọn được hai phân số để được tử số là 1 và mẫu số khác nhau.
Lời giải chi tiết:
\(\frac{{11}}{{30}} = \frac{5}{{30}} + \frac{6}{{30}} = \frac{1}{6} + \frac{1}{5}\)
Viết phân số \(\frac{{11}}{{30}}\) thành tổng hai phân số có tử số là 1 và mẫu số khác nhau.
Phương pháp giải:
Tách tử số của phân số đã cho thành tổng sao cho rút gọn được hai phân số để được tử số là 1 và mẫu số khác nhau.
Lời giải chi tiết:
\(\frac{{11}}{{30}} = \frac{5}{{30}} + \frac{6}{{30}} = \frac{1}{6} + \frac{1}{5}\)
Hoàn thành các tháp số sau (theo mẫu):
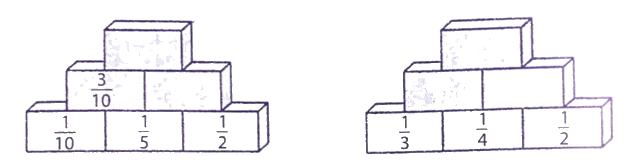
Phương pháp giải:
Quy luật: Tổng hai ô liên tiếp là kết quả của số ở giữa thuộc hàng trên.
Lời giải chi tiết:
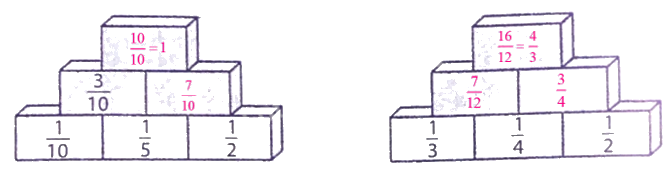
Cách đây khoảng 4000 năm, người Ai Cập đã hiểu được phân số và biết các phép tính về phân số. Tuy nhiên, người Ai Cập cổ chỉ thừa nhận các phân số có tử số là 1. Vì vậy, phân số có tử số là 1 còn được gọi là phân số Ai Cập. Phân số \(\frac{5}{6}\) được viết dưới dạng phân số Ai Cập như sau: \(\frac{5}{6} = \frac{1}{2} + \frac{1}{3}\).
Viết phân số \(\frac{7}{{10}}\) dưới dạng tổng các phân số Ai Cập.
Phương pháp giải:
Tách phân số $\frac{7}{{10}}$thành tổng sao cho rút gọn được hai phân số để có tử số là 1.
Lời giải chi tiết:
\(\frac{7}{{10}} = \frac{2}{{10}} + \frac{5}{{10}} = \frac{1}{5} + \frac{1}{2}\)
Hoàn thành các tháp số sau (theo mẫu):
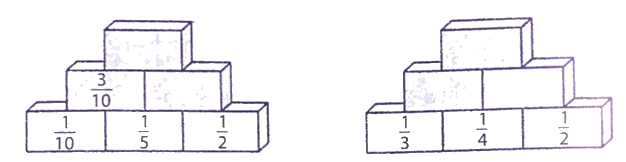
Phương pháp giải:
Quy luật: Tổng hai ô liên tiếp là kết quả của số ở giữa thuộc hàng trên.
Lời giải chi tiết:
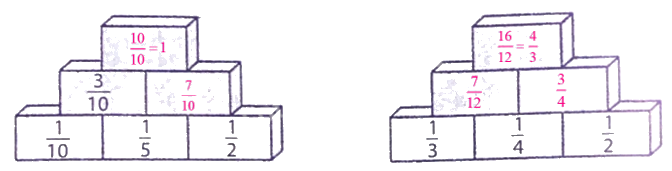
Phần C. Vận dụng, phát triển trang 17 trong sách Bài tập phát triển năng lực Toán 4 tập 2 thường chứa các bài toán yêu cầu học sinh áp dụng kiến thức đã học vào các tình huống thực tế, hoặc mở rộng, nâng cao kiến thức. Các bài toán này không chỉ kiểm tra khả năng tính toán mà còn đánh giá khả năng tư duy logic, phân tích và giải quyết vấn đề của học sinh.
Để giúp các em hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng bài toán trong phần C:
Đề bài: (Giả sử đề bài là: Một cửa hàng có 35 kg gạo tẻ và 28 kg gạo nếp. Hỏi cửa hàng có tất cả bao nhiêu ki-lô-gam gạo?)
Lời giải:
Cửa hàng có tất cả số ki-lô-gam gạo là:
35 + 28 = 63 (kg)
Đáp số: 63 kg
Đề bài: (Giả sử đề bài là: Một hình chữ nhật có chiều dài 12cm và chiều rộng 8cm. Tính chu vi và diện tích của hình chữ nhật đó.)
Lời giải:
Chu vi của hình chữ nhật là:
(12 + 8) x 2 = 40 (cm)
Diện tích của hình chữ nhật là:
12 x 8 = 96 (cm2)
Đáp số: Chu vi: 40cm; Diện tích: 96cm2
Để giải các bài toán trong phần C. Vận dụng, phát triển trang 17 một cách hiệu quả, các em cần:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể tự giải thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online. Việc luyện tập thường xuyên sẽ giúp các em tự tin hơn khi làm bài kiểm tra.
Đừng ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn trong quá trình giải toán. Việc trao đổi, thảo luận sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải toán.
| Công thức | Mô tả |
|---|---|
| Chu vi hình chữ nhật | (Chiều dài + Chiều rộng) x 2 |
| Diện tích hình chữ nhật | Chiều dài x Chiều rộng |
| Tổng | Số hạng 1 + Số hạng 2 |
Hy vọng với bài giải chi tiết này, các em sẽ hiểu rõ hơn về phần C. Vận dụng, phát triển trang 17 Toán 4 tập 2 và đạt kết quả tốt trong học tập.