Chào mừng các em học sinh đến với chuyên mục giải bài tập phát triển năng lực Toán 4 tập 2 của giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho phần C. Vận dụng, phát triển trang 53, giúp các em hiểu rõ bản chất bài toán và rèn luyện kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng, việc làm bài tập phát triển năng lực đòi hỏi sự tư duy sáng tạo và vận dụng kiến thức đã học vào thực tế. Do đó, giaitoan.edu.vn luôn cố gắng trình bày lời giải một cách rõ ràng, logic, kèm theo các giải thích chi tiết để các em có thể tự học và nắm vững kiến thức.
Xoài ba màu là cây ăn trái được người dân tỉnh An Giang nhân giống .... Hai bạn Thắng và Chiến chơi đố vui về phân số. Có các phân số 4/13
Hai bạn Thắng và Chiến chơi đố vui về phân số. Có các phân số: $\frac{4}{{13}};\frac{1}{{18}};\frac{7}{5};\frac{2}{{13}};\frac{7}{3};\frac{4}{5};\frac{7}{4}$.
Thắng tìm hai phân số có tổng nhỏ nhất. Chiến tìm hai phân số có tổng lớn nhất. Em hãy tính tổng bốn phân số đó.
Phương pháp giải:
Bước 1: So sánh các phân số đã cho để tìm ra 2 phân số bé nhất; 2 phân số lớn nhất.
Bước 2: Tính tổng 4 phân số vừa tìm được.
Lời giải chi tiết:
Ta có:
+) $\frac{7}{5};\frac{7}{3};\frac{7}{4}$ đều lớn hơn 1 và $\frac{7}{5} < \frac{7}{4} < \frac{7}{3}$
+) $\frac{4}{{13}};\frac{1}{{18}};\frac{2}{{13}};\frac{4}{5}$ đều nhỏ hơn 1 và $\frac{1}{{18}} < \frac{2}{{13}} < \frac{4}{{13}} < \frac{4}{5}$.
Tổng phân số mà bạn Thắng tìm là $\frac{1}{{18}} + \frac{2}{{13}} = \frac{{13}}{{234}} + \frac{{36}}{{234}} = \frac{{49}}{{234}}$
Tổng phân số mà bạn Chiến tìm là: $\frac{7}{4} + \frac{7}{3} = \frac{{21}}{{12}} + \frac{{28}}{{12}} = \frac{{49}}{{12}}$
Vậy tổng của 4 phân số tìm được là: $\frac{{49}}{{234}} + \frac{{49}}{{12}} = \frac{{2009}}{{468}}$
Viết vào chỗ trống cho phù hợp:
Hai Bà Trưng khởi nghĩa vào năm 40, năm đó thuộc thế kỉ ................
Chiến thắng Bạch Đằng vào năm 938, năm đó thuộc thế kỉ .................
Chiến thắng Điện Biên Phủ vào năm 1954, năm đó thuộc thế kỉ ..............
Phương pháp giải:
- Từ năm 1 đến năm 100 là thế kỉ một (thế kỉ I)
- Từ năm 101 đến năm 200 là thế kỉ hai (thế kỉ II)
- Từ năm 201 đến năm 300 là thế kỉ ba (thế kỉ III)
...............
Lời giải chi tiết:
Hai Bà Trưng khởi nghĩa vào năm 40, năm đó thuộc thế kỉ I.
Chiến thắng Bạch Đằng vào năm 938, năm đó thuộc thế kỉ X.
Chiến thắng Điện Biên Phủ vào năm 1954, năm đó thuộc thế kỉ XX.
Xoài ba màu là cây ăn trái được người dân tỉnh An Giang nhân giống. Khi còn nhỏ, trái xoài có màu xanh, già đổi sang tím, chín lại chuyển vàng. Quả xoài to có thể nặng đến 1kg. Xoài ba màu trồng chủ yếu ở huyện Chợ Mới. Cứ 100m2 thu hoạch được 150kg xoài, càng lâu năm thì sản lượng càng cao.
Huyện Chợ Mới có khoảng 15km2 xoài ba màu. Hiện nay, xoài ba màu có giá bán trung bình 24 000 đồng mỗi ki-lô-gam, mang lại thu nhập cao cho nhiều hộ nông dân.
(Theo vnexpess.net)
a) Tính khối lượng xoài thu hoạch được trên 10 000m2.
b) Ước tính thu nhập trung bình từ trồng xoài ba màu trên 10 000m2.
Phương pháp giải:
a) Khối lượng xoài thu hoạch được= số kg xoài thu hoạch trên 100m2 x (diện tích trồng xoài : 100)
b) Thu nhập trung bình từ trồng xoài ba màu trên 10 000m2 = giá xoài trung bình x khối lượng xoài thu hoạch được trên 10 000m2
Lời giải chi tiết:
a) Khối lượng xoài thu hoạch được trên 10 000m2 là
150 x (10 000 : 100) = 15 000 (kg)
b) Thu nhập trung bình từ trồng xoài ba màu trên 10 000m2 là:
24 000 x 15 000 = 360 000 000 (đồng)
Đáp số: a) 15 000 kg; b) 360 000 000 đồng
Phân số?
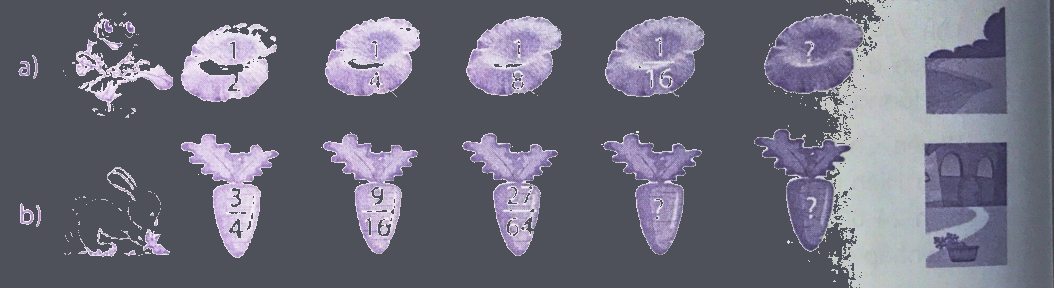
Phương pháp giải:
a) Phân số đằng sau = Phân số đằng trước x $\frac{1}{2}$
b) Phân số đằng sau = Phân số đằng trước x $\frac{3}{4}$
Lời giải chi tiết:
a) Quy luật: Phân số đằng sau = Phân số đằng trước x $\frac{1}{2}$
Phân số cần điền vào dấu ? là: $\frac{1}{{16}} \times \frac{1}{2} = \frac{1}{{32}}$
b) Quy luật: Phân số đằng sau = Phân số đằng trước x $\frac{3}{4}$
Phân số cần điền vào dấu ? là: $\frac{{27}}{{64}} \times \frac{3}{4} = \frac{{81}}{{256}}$;$\frac{{81}}{{256}} \times \frac{3}{4} = \frac{{234}}{{1024}}$
Xoài ba màu là cây ăn trái được người dân tỉnh An Giang nhân giống. Khi còn nhỏ, trái xoài có màu xanh, già đổi sang tím, chín lại chuyển vàng. Quả xoài to có thể nặng đến 1kg. Xoài ba màu trồng chủ yếu ở huyện Chợ Mới. Cứ 100m2 thu hoạch được 150kg xoài, càng lâu năm thì sản lượng càng cao.
Huyện Chợ Mới có khoảng 15km2 xoài ba màu. Hiện nay, xoài ba màu có giá bán trung bình 24 000 đồng mỗi ki-lô-gam, mang lại thu nhập cao cho nhiều hộ nông dân.
(Theo vnexpess.net)
a) Tính khối lượng xoài thu hoạch được trên 10 000m2.
b) Ước tính thu nhập trung bình từ trồng xoài ba màu trên 10 000m2.
Phương pháp giải:
a) Khối lượng xoài thu hoạch được= số kg xoài thu hoạch trên 100m2 x (diện tích trồng xoài : 100)
b) Thu nhập trung bình từ trồng xoài ba màu trên 10 000m2 = giá xoài trung bình x khối lượng xoài thu hoạch được trên 10 000m2
Lời giải chi tiết:
a) Khối lượng xoài thu hoạch được trên 10 000m2 là
150 x (10 000 : 100) = 15 000 (kg)
b) Thu nhập trung bình từ trồng xoài ba màu trên 10 000m2 là:
24 000 x 15 000 = 360 000 000 (đồng)
Đáp số: a) 15 000 kg; b) 360 000 000 đồng
Hai bạn Thắng và Chiến chơi đố vui về phân số. Có các phân số: $\frac{4}{{13}};\frac{1}{{18}};\frac{7}{5};\frac{2}{{13}};\frac{7}{3};\frac{4}{5};\frac{7}{4}$.
Thắng tìm hai phân số có tổng nhỏ nhất. Chiến tìm hai phân số có tổng lớn nhất. Em hãy tính tổng bốn phân số đó.
Phương pháp giải:
Bước 1: So sánh các phân số đã cho để tìm ra 2 phân số bé nhất; 2 phân số lớn nhất.
Bước 2: Tính tổng 4 phân số vừa tìm được.
Lời giải chi tiết:
Ta có:
+) $\frac{7}{5};\frac{7}{3};\frac{7}{4}$ đều lớn hơn 1 và $\frac{7}{5} < \frac{7}{4} < \frac{7}{3}$
+) $\frac{4}{{13}};\frac{1}{{18}};\frac{2}{{13}};\frac{4}{5}$ đều nhỏ hơn 1 và $\frac{1}{{18}} < \frac{2}{{13}} < \frac{4}{{13}} < \frac{4}{5}$.
Tổng phân số mà bạn Thắng tìm là $\frac{1}{{18}} + \frac{2}{{13}} = \frac{{13}}{{234}} + \frac{{36}}{{234}} = \frac{{49}}{{234}}$
Tổng phân số mà bạn Chiến tìm là: $\frac{7}{4} + \frac{7}{3} = \frac{{21}}{{12}} + \frac{{28}}{{12}} = \frac{{49}}{{12}}$
Vậy tổng của 4 phân số tìm được là: $\frac{{49}}{{234}} + \frac{{49}}{{12}} = \frac{{2009}}{{468}}$
Viết vào chỗ trống cho phù hợp:
Hai Bà Trưng khởi nghĩa vào năm 40, năm đó thuộc thế kỉ ................
Chiến thắng Bạch Đằng vào năm 938, năm đó thuộc thế kỉ .................
Chiến thắng Điện Biên Phủ vào năm 1954, năm đó thuộc thế kỉ ..............
Phương pháp giải:
- Từ năm 1 đến năm 100 là thế kỉ một (thế kỉ I)
- Từ năm 101 đến năm 200 là thế kỉ hai (thế kỉ II)
- Từ năm 201 đến năm 300 là thế kỉ ba (thế kỉ III)
...............
Lời giải chi tiết:
Hai Bà Trưng khởi nghĩa vào năm 40, năm đó thuộc thế kỉ I.
Chiến thắng Bạch Đằng vào năm 938, năm đó thuộc thế kỉ X.
Chiến thắng Điện Biên Phủ vào năm 1954, năm đó thuộc thế kỉ XX.
Phân số?
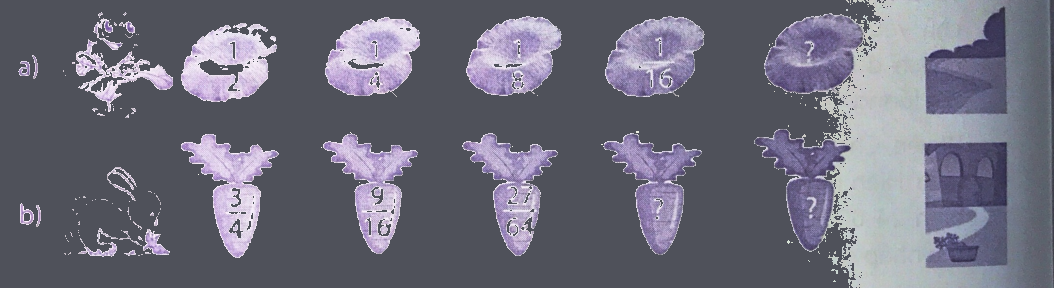
Phương pháp giải:
a) Phân số đằng sau = Phân số đằng trước x $\frac{1}{2}$
b) Phân số đằng sau = Phân số đằng trước x $\frac{3}{4}$
Lời giải chi tiết:
a) Quy luật: Phân số đằng sau = Phân số đằng trước x $\frac{1}{2}$
Phân số cần điền vào dấu ? là: $\frac{1}{{16}} \times \frac{1}{2} = \frac{1}{{32}}$
b) Quy luật: Phân số đằng sau = Phân số đằng trước x $\frac{3}{4}$
Phân số cần điền vào dấu ? là: $\frac{{27}}{{64}} \times \frac{3}{4} = \frac{{81}}{{256}}$;$\frac{{81}}{{256}} \times \frac{3}{4} = \frac{{234}}{{1024}}$
Bài tập phát triển năng lực Toán 4 tập 2 trang 53 tập trung vào việc rèn luyện khả năng vận dụng kiến thức đã học vào giải quyết các bài toán thực tế, đòi hỏi học sinh phải có tư duy logic và khả năng phân tích vấn đề. Dưới đây là lời giải chi tiết cho từng bài tập:
Đề bài: (Nêu lại đề bài đầy đủ)
Lời giải:
Giải thích: (Giải thích chi tiết từng bước giải, giúp học sinh hiểu rõ bản chất bài toán)
Đề bài: (Nêu lại đề bài đầy đủ)
Lời giải:
Giải thích: (Giải thích chi tiết từng cách giải, so sánh ưu nhược điểm của từng phương pháp)
Đề bài: (Nêu lại đề bài đầy đủ)
Lời giải:
(Giải bài toán chi tiết)
Giải thích: (Giải thích chi tiết)
Ngoài việc giải các bài tập trong sách giáo khoa, các em có thể tìm hiểu thêm các bài tập tương tự trên internet hoặc trong các sách bài tập tham khảo. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán một cách hiệu quả.
Hy vọng rằng, với lời giải chi tiết và những hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập phát triển năng lực Toán 4 tập 2 trang 53. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Lời giải | Giải thích |
|---|---|---|
| Bài 1 | (Tóm tắt lời giải) | (Tóm tắt giải thích) |
| Bài 2 | (Tóm tắt lời giải) | (Tóm tắt giải thích) |
| Bài 3 | (Tóm tắt lời giải) | (Tóm tắt giải thích) |