Chào mừng các em học sinh đến với bài giải chi tiết phần A. Tái hiện, củng cố trang 12 trong sách Bài tập phát triển năng lực Toán 4 tập 2. Bài học này giúp các em ôn lại kiến thức đã học và rèn luyện kỹ năng giải toán một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Rút gọn các phân số theo mẫu (theo mẫu) .... Điền dấu (>; <; =) thích hợp vào ô trống:
Quy đồng mẫu số các phân số:
a) \(\frac{9}{7}\) và$\frac{8}{5}$
b) $\frac{5}{{18}}$ và $\frac{9}{{10}}$
c) \(\frac{5}{{22}}\) và$\frac{7}{{33}}$
d) $\frac{3}{{12}}$ và $\frac{7}{{20}}$
Phương pháp giải:
- Tìm mẫu số chung
- Tìm thừa số phụ bằng cách lấy mẫu số chung chia cho mẫu số của mỗi phân số
- Nhân cả tử số và mẫu số của mỗi phân số với thừa số phụ vừa tìm được.
Lời giải chi tiết:
a) \(\frac{9}{7}\) và$\frac{8}{5}$
Ta có $\frac{9}{7} = \frac{{9 \times 5}}{{7 \times 5}} = \frac{{45}}{{35}}$ ; \(\frac{8}{5} = \frac{{8 \times 7}}{{5 \times 7}} = \frac{{56}}{{35}}\)
Vậy quy đồng mẫu số của \(\frac{9}{7}\) và$\frac{8}{5}$ được \(\frac{{45}}{{35}}\) và$\frac{{56}}{{35}}$.
b) $\frac{5}{{18}}$ và $\frac{9}{{10}}$
Ta có: \(\frac{5}{{18}} = \frac{{5 \times 5}}{{18 \times 5}} = \frac{{25}}{{90}}\) ; \(\frac{9}{{10}} = \frac{{9 \times 9}}{{10 \times 9}} = \frac{{81}}{{90}}\)
Vậy quy đồng mẫu số của$\frac{5}{{18}}$ và $\frac{9}{{10}}$ được \(\frac{{25}}{{90}}\) và$\frac{{81}}{{90}}$.
c) \(\frac{5}{{22}}\) và$\frac{7}{{33}}$
Ta có $\frac{5}{{22}} = \frac{{5 \times 3}}{{22 \times 3}} = \frac{{15}}{{66}}$ ; \(\frac{7}{{33}} = \frac{{7 \times 2}}{{33 \times 2}} = \frac{{14}}{{66}}\)
Vậy quy đồng mẫu số của \(\frac{5}{{22}}\) và$\frac{7}{{33}}$ được \(\frac{{15}}{{66}}\) và$\frac{{14}}{{66}}$.
d) $\frac{3}{{12}}$ và $\frac{7}{{20}}$
Ta có $\frac{3}{{12}} = \frac{{3 \times 5}}{{12 \times 5}} = \frac{{15}}{{60}}$ ; \(\frac{7}{{20}} = \frac{{7 \times 3}}{{20 \times 3}} = \frac{{21}}{{60}}\)
Vậy quy đồng mẫu số của $\frac{3}{{12}}$ và $\frac{7}{{20}}$được \(\frac{{15}}{{60}}\) và$\frac{{21}}{{60}}$.
Rút gọn các phân số theo mẫu (theo mẫu):
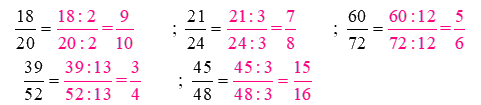
Phương pháp giải:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
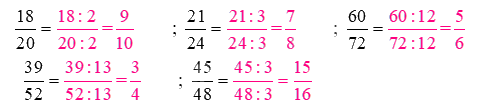
Điền dấu (>; <; =) thích hợp vào ô trống:

Phương pháp giải:
Bước 1: Quy đồng mẫu số hai phân số.
Bước 2: So sánh hai phân số có cùng mẫu số đó.
Bước 3: Rút ra kết luận.
Lời giải chi tiết:
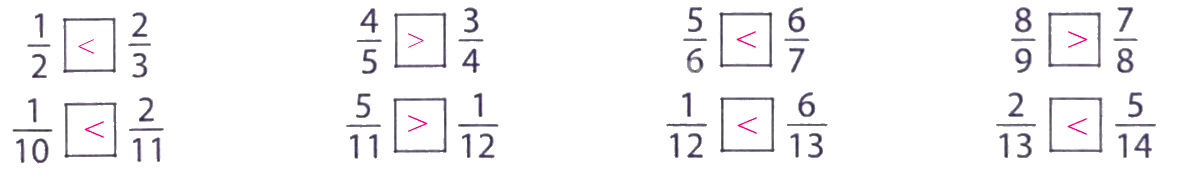
Điền dấu (>; <; =) thích hợp vào ô trống:
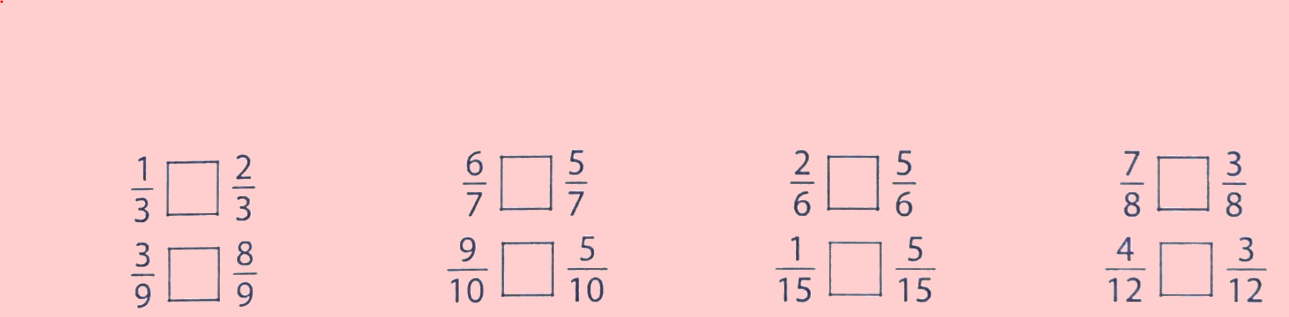
Phương pháp giải:
Trong hai phân số có cùng mẫu số:
+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.
+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Lời giải chi tiết:
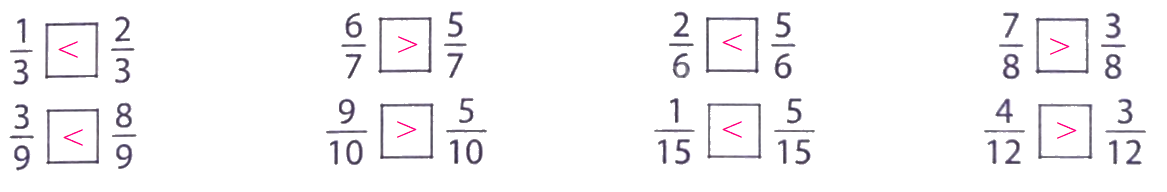
Điền dấu (>; <; =) thích hợp vào ô trống:
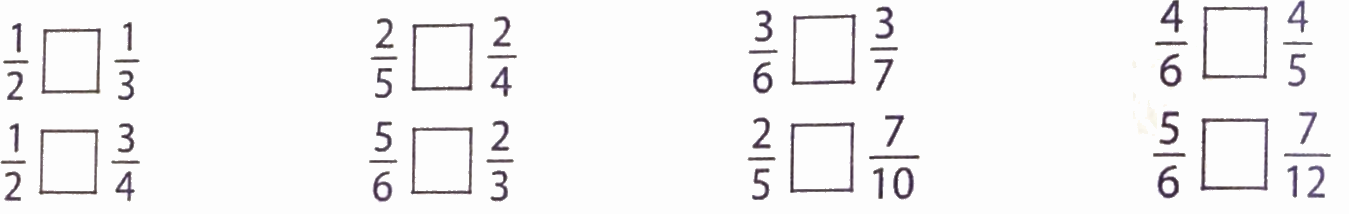
Phương pháp giải:
- Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.
Lời giải chi tiết:
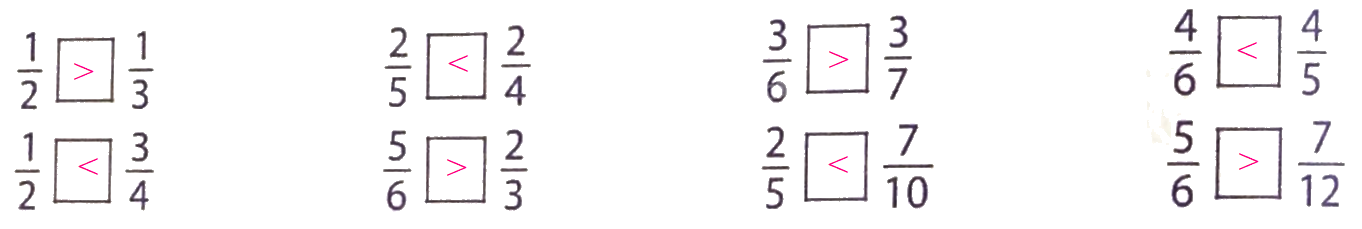
Rút gọn các phân số theo mẫu (theo mẫu):
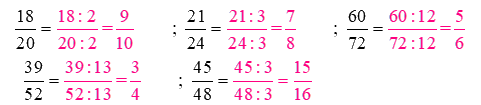
Phương pháp giải:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
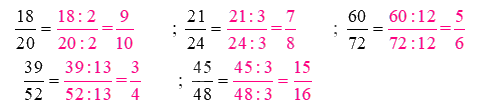
Quy đồng mẫu số các phân số:
a) \(\frac{9}{7}\) và$\frac{8}{5}$
b) $\frac{5}{{18}}$ và $\frac{9}{{10}}$
c) \(\frac{5}{{22}}\) và$\frac{7}{{33}}$
d) $\frac{3}{{12}}$ và $\frac{7}{{20}}$
Phương pháp giải:
- Tìm mẫu số chung
- Tìm thừa số phụ bằng cách lấy mẫu số chung chia cho mẫu số của mỗi phân số
- Nhân cả tử số và mẫu số của mỗi phân số với thừa số phụ vừa tìm được.
Lời giải chi tiết:
a) \(\frac{9}{7}\) và$\frac{8}{5}$
Ta có $\frac{9}{7} = \frac{{9 \times 5}}{{7 \times 5}} = \frac{{45}}{{35}}$ ; \(\frac{8}{5} = \frac{{8 \times 7}}{{5 \times 7}} = \frac{{56}}{{35}}\)
Vậy quy đồng mẫu số của \(\frac{9}{7}\) và$\frac{8}{5}$ được \(\frac{{45}}{{35}}\) và$\frac{{56}}{{35}}$.
b) $\frac{5}{{18}}$ và $\frac{9}{{10}}$
Ta có: \(\frac{5}{{18}} = \frac{{5 \times 5}}{{18 \times 5}} = \frac{{25}}{{90}}\) ; \(\frac{9}{{10}} = \frac{{9 \times 9}}{{10 \times 9}} = \frac{{81}}{{90}}\)
Vậy quy đồng mẫu số của$\frac{5}{{18}}$ và $\frac{9}{{10}}$ được \(\frac{{25}}{{90}}\) và$\frac{{81}}{{90}}$.
c) \(\frac{5}{{22}}\) và$\frac{7}{{33}}$
Ta có $\frac{5}{{22}} = \frac{{5 \times 3}}{{22 \times 3}} = \frac{{15}}{{66}}$ ; \(\frac{7}{{33}} = \frac{{7 \times 2}}{{33 \times 2}} = \frac{{14}}{{66}}\)
Vậy quy đồng mẫu số của \(\frac{5}{{22}}\) và$\frac{7}{{33}}$ được \(\frac{{15}}{{66}}\) và$\frac{{14}}{{66}}$.
d) $\frac{3}{{12}}$ và $\frac{7}{{20}}$
Ta có $\frac{3}{{12}} = \frac{{3 \times 5}}{{12 \times 5}} = \frac{{15}}{{60}}$ ; \(\frac{7}{{20}} = \frac{{7 \times 3}}{{20 \times 3}} = \frac{{21}}{{60}}\)
Vậy quy đồng mẫu số của $\frac{3}{{12}}$ và $\frac{7}{{20}}$được \(\frac{{15}}{{60}}\) và$\frac{{21}}{{60}}$.
Điền dấu (>; <; =) thích hợp vào ô trống:
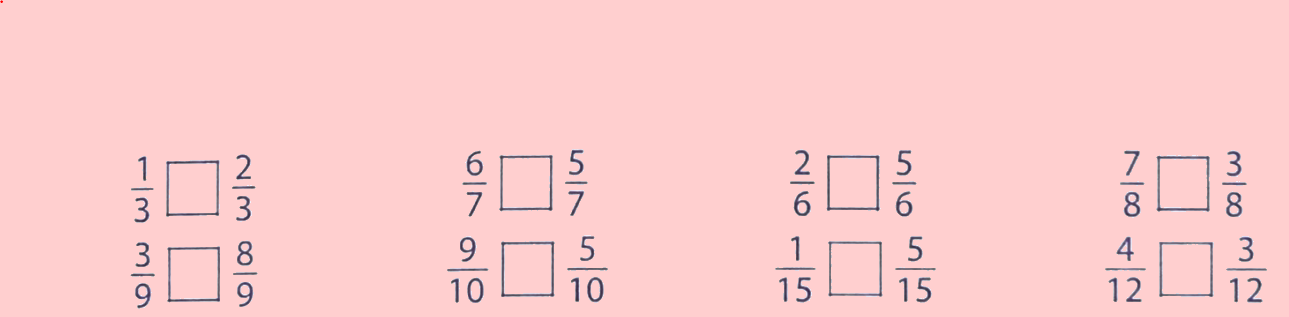
Phương pháp giải:
Trong hai phân số có cùng mẫu số:
+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.
+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Lời giải chi tiết:
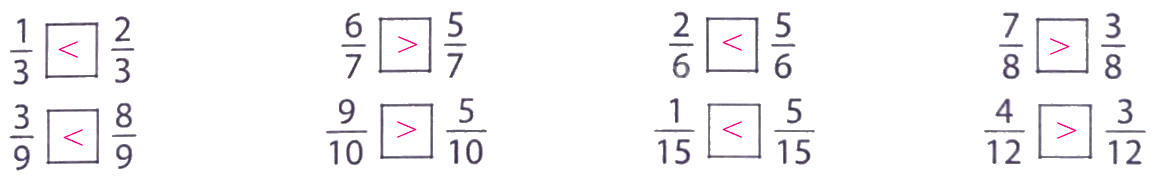
Điền dấu (>; <; =) thích hợp vào ô trống:

Phương pháp giải:
Bước 1: Quy đồng mẫu số hai phân số.
Bước 2: So sánh hai phân số có cùng mẫu số đó.
Bước 3: Rút ra kết luận.
Lời giải chi tiết:
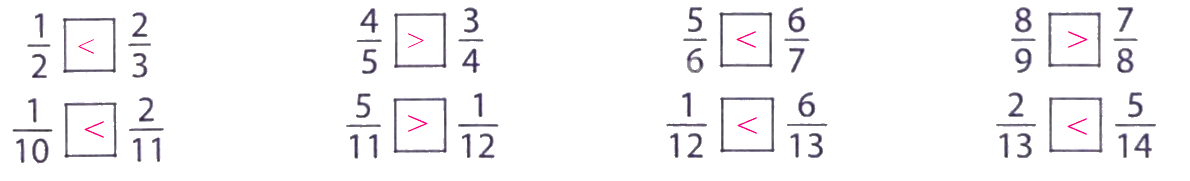
Điền dấu (>; <; =) thích hợp vào ô trống:
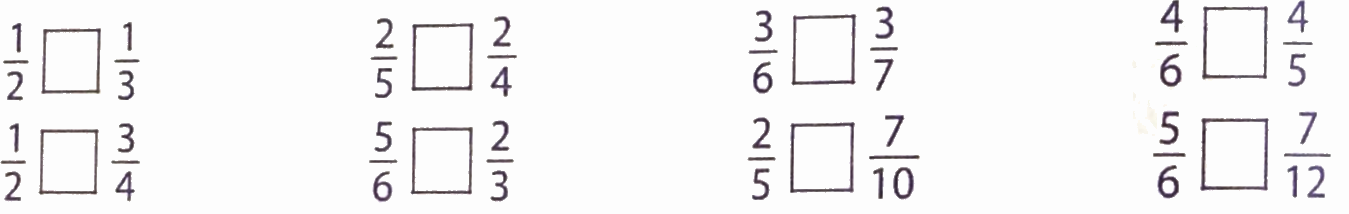
Phương pháp giải:
- Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.
Lời giải chi tiết:
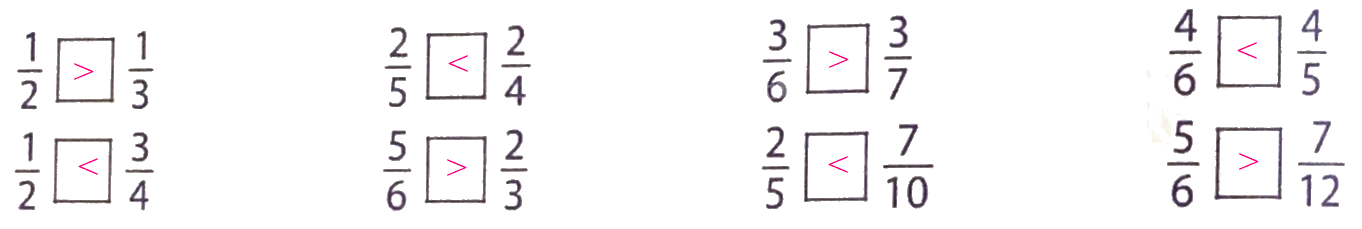
Phần A. Tái hiện, củng cố trang 12 trong Bài tập phát triển năng lực Toán 4 tập 2 tập trung vào việc giúp học sinh củng cố kiến thức về các phép tính cơ bản, đặc biệt là phép cộng, trừ, nhân, chia trong phạm vi 100.000. Các bài tập trong phần này thường được trình bày dưới dạng các bài toán thực tế, đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết.
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia. Để giải bài này, học sinh cần nắm vững các quy tắc thực hiện các phép tính và thực hiện tính toán một cách cẩn thận. Ví dụ:
Bài 2 thường là các bài toán có lời văn, yêu cầu học sinh đọc kỹ đề bài, xác định được các dữ kiện và yêu cầu của bài toán, sau đó lập kế hoạch giải và thực hiện giải bài toán. Ví dụ:
Một cửa hàng có 250 kg gạo. Buổi sáng cửa hàng bán được 120 kg gạo, buổi chiều bán được 80 kg gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Giải:
Tổng số gạo đã bán là: 120 + 80 = 200 (kg)
Số gạo còn lại là: 250 - 200 = 50 (kg)
Đáp số: 50 kg
Bài 3 yêu cầu học sinh tìm giá trị của x trong các biểu thức toán học. Để giải bài này, học sinh cần sử dụng các quy tắc chuyển vế và thực hiện các phép tính để tìm ra giá trị của x. Ví dụ:
x + 123 = 456
x = 456 - 123
x = 333
Việc luyện tập thường xuyên là yếu tố quan trọng để học sinh nắm vững kiến thức và kỹ năng giải toán. Các em nên dành thời gian làm bài tập đầy đủ và thường xuyên ôn tập lại kiến thức đã học. Ngoài ra, các em cũng có thể tham gia các câu lạc bộ toán học hoặc các lớp học thêm để nâng cao khả năng giải toán của mình.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các bài giải chi tiết, đáp án chính xác và các tài liệu học tập hữu ích cho học sinh. Chúng tôi luôn cố gắng tạo ra một môi trường học tập thân thiện và hiệu quả, giúp các em học toán một cách dễ dàng và thú vị.
| Dạng bài tập | Mục tiêu |
|---|---|
| Giải các phép tính | Rèn luyện kỹ năng tính toán |
| Giải bài toán có lời văn | Vận dụng kiến thức vào thực tế |
| Tìm x | Hiểu và áp dụng các quy tắc đại số |
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết phần A. Tái hiện, củng cố trang 12 Toán 4 tập 2 một cách hiệu quả. Chúc các em học tốt!