Chào mừng các em học sinh lớp 4 đến với chuyên mục giải bài tập Toán 4 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập phần A: Tái hiện, củng cố trang 2, 3 sách Toán 4, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn cung cấp lời giải chính xác, dễ hiểu, cùng với phương pháp giải bài tập hiệu quả, giúp các em tự tin hơn trong học tập.
Viết tiếp các số thích hợp vào chỗ chấm: 55 270; 55 280; ..........; ..........; 55 310; ..........Tính giá trị của biểu thức: a) 2 019 + m : 2 với m = 382; m = 2 020.
Viết tiếp các số thích hợp vào chỗ chấm:
55 270; 55 280; ..........; ..........; 55 310; ..........
44 054; ..........; ..........; 44 354; ..........; 44 554.
11 943; 12 943; ..........; ..........; 15 943; ..........
Phương pháp giải:
Đếm thêm 10, 100, 1 000 đơn vị rồi điền số còn thiếu vào chỗ trống.
Lời giải chi tiết:
55 270; 55 280; 55 290; 55 300; 55 310; 55 320.
44 054; 44 154; 44 254; 44 354; 44 454; 44 554.
11 943; 12 943; 13 943; 14 943; 15 943; 16 943.
Tính nhẩm:
58 300 – 12 300 = .......................
26 780 – 6 780 = .......................
29 000 x 2 = .......................
46 000 + 14 000 = .......................
41 450 + 8 550 = .......................
36 000 : 4 = .......................
Phương pháp giải:
Học sinh có thể nhẩm như sau: 3 trăm – 3 trăm = 0
58 nghìn - 12 nghìn = 46 nghìn.
Và ghi kết quả: 58 300 – 12 300 = 46 000
Nhẩm tương tự với các câu còn lại.
Lời giải chi tiết:
58 300 – 12 300 = 46 000
26 780 – 6 780 = 20 000
29 000 x 2 = 58 000
46 000 + 14 000 = 60 000
41 450 + 8 550 = 50 000
36 000 : 4 = 9 000
Tính giá trị của biểu thức:
a) 2 019 + m : 2 với m = 382; m = 2 020.
b) n x 3 + 5 190 với n = 106; n = 2 010.
c) (2 315 + p) : 5 – 565 với p = 510; p = 715.
Phương pháp giải:
Thay giá trị của chữ vào biểu thức rồi tính giá trị biểu thức đó.
Lời giải chi tiết:
a) Nếu m = 382 thì 2 019 + m : 2 = 2 019 + 382 : 2 = 2 019 + 191 = 2 210.
Nếu m = 2 020 thì 2 019 + m : 2 = 2 019 + 2 020 : 2 = 2 019 + 1 010 = 3 029.
b) Nếu n = 106 thì n x 3 + 5 190 = 106 x 3 + 5 190 = 318 + 5 190 = 5 508.
Nếu n = 2 010 thì n x 3 + 5 190 = 2 010 x 3 + 5 190 = 6 030 + 5 190 = 11 220.
c) Nếu p = 510 thì (2 315 + p) : 5 – 565 = (2 315 + 510) : 5 – 565
= 2 820 : 5 – 565
= 565 – 565 = 0.
Nếu p = 715 thì (2 315 + p) : 5 = (2 315 + 715) : 5 – 565
= 3 030 : 5 – 565
= 606 – 565 = 41.
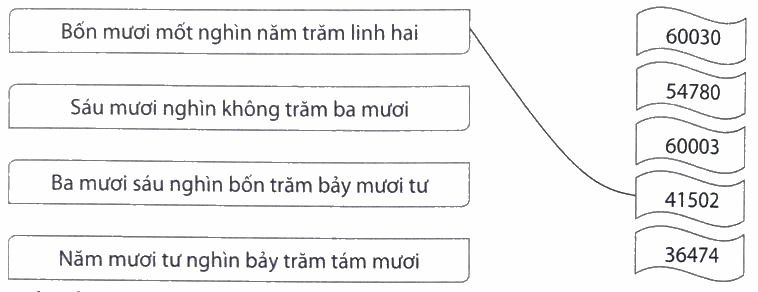
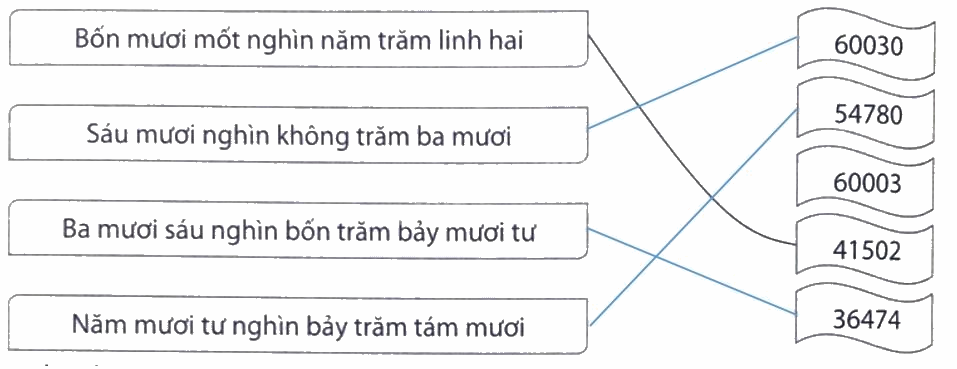
Nối (theo mẫu).
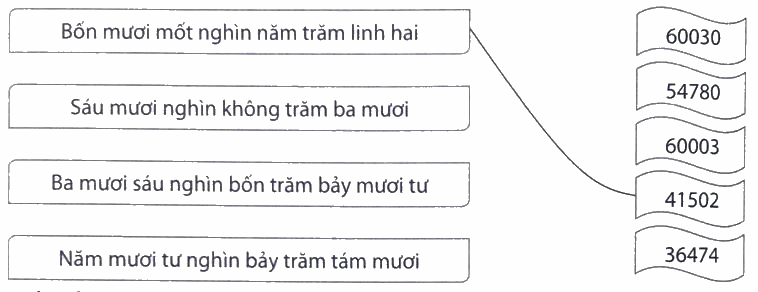
Phương pháp giải:
Đọc số theo thứ tự từ hàng chục nghìn, hàng nghìn, hàng trăm, hàng chục, hàng đơn vị.
Lời giải chi tiết:
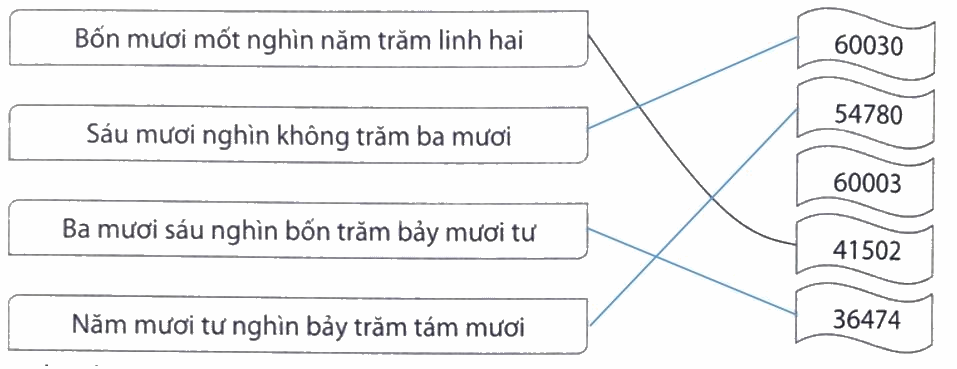
Đặt tính rồi tính.
74 181 + 4 728 48 086 – 22 248
13 073 x 3 15 832 : 4
Phương pháp giải:
Đặt tính rồi tính theo các quy tắc đã học.
Lời giải chi tiết:
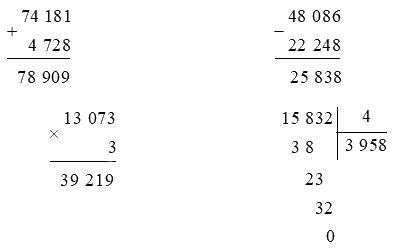
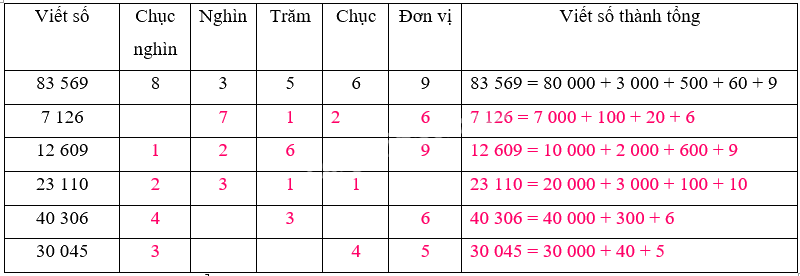
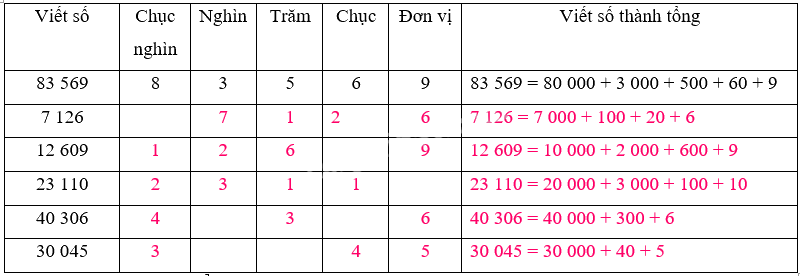
Viết (theo mẫu):
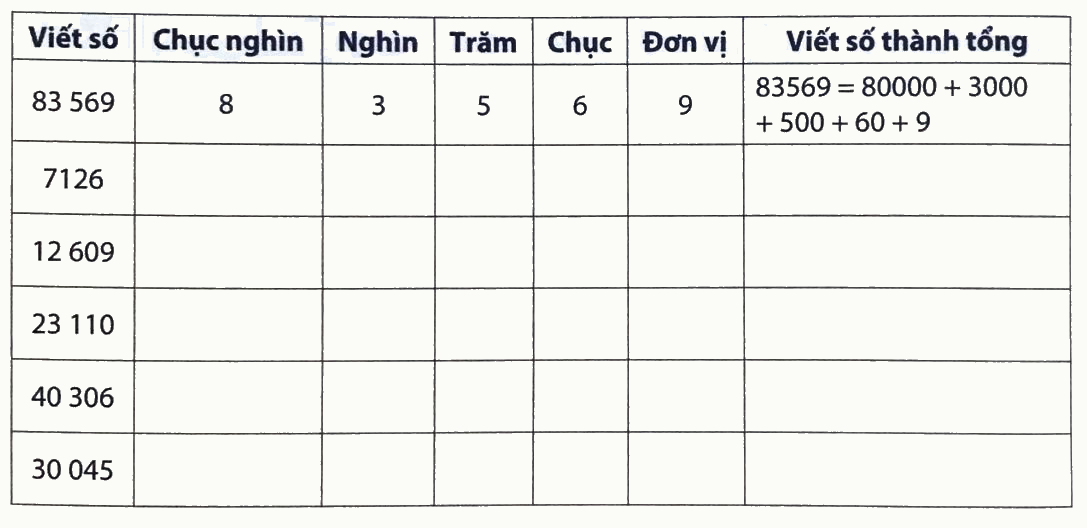
Phương pháp giải:
Viết các số thành tổng của chục nghìn, nghìn, trăm, chục và đơn vị theo mẫu.
Lời giải chi tiết:
Nối (theo mẫu).
Phương pháp giải:
Đọc số theo thứ tự từ hàng chục nghìn, hàng nghìn, hàng trăm, hàng chục, hàng đơn vị.
Lời giải chi tiết:
Viết tiếp các số thích hợp vào chỗ chấm:
55 270; 55 280; ..........; ..........; 55 310; ..........
44 054; ..........; ..........; 44 354; ..........; 44 554.
11 943; 12 943; ..........; ..........; 15 943; ..........
Phương pháp giải:
Đếm thêm 10, 100, 1 000 đơn vị rồi điền số còn thiếu vào chỗ trống.
Lời giải chi tiết:
55 270; 55 280; 55 290; 55 300; 55 310; 55 320.
44 054; 44 154; 44 254; 44 354; 44 454; 44 554.
11 943; 12 943; 13 943; 14 943; 15 943; 16 943.
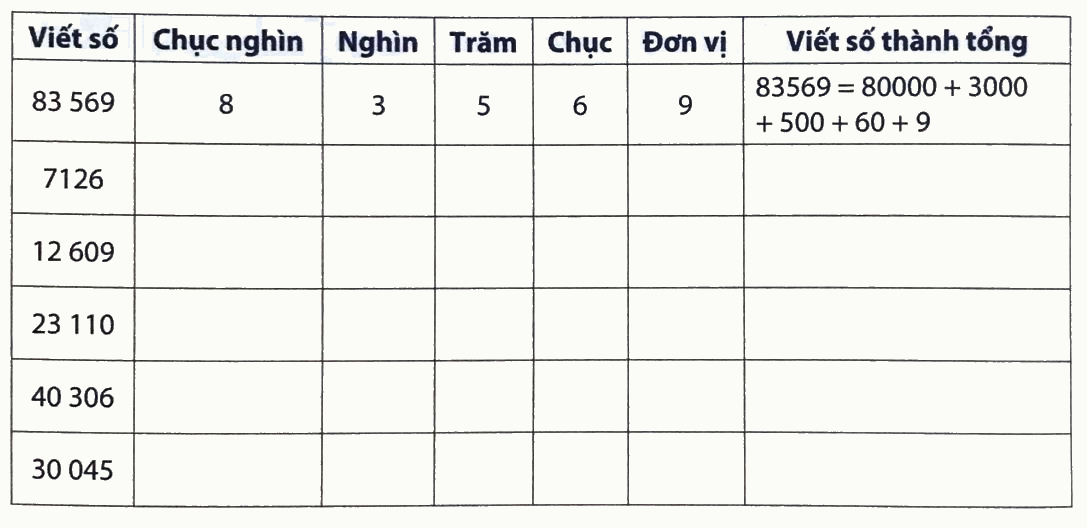
Viết (theo mẫu):
Phương pháp giải:
Viết các số thành tổng của chục nghìn, nghìn, trăm, chục và đơn vị theo mẫu.
Lời giải chi tiết:
Tính nhẩm:
58 300 – 12 300 = .......................
26 780 – 6 780 = .......................
29 000 x 2 = .......................
46 000 + 14 000 = .......................
41 450 + 8 550 = .......................
36 000 : 4 = .......................
Phương pháp giải:
Học sinh có thể nhẩm như sau: 3 trăm – 3 trăm = 0
58 nghìn - 12 nghìn = 46 nghìn.
Và ghi kết quả: 58 300 – 12 300 = 46 000
Nhẩm tương tự với các câu còn lại.
Lời giải chi tiết:
58 300 – 12 300 = 46 000
26 780 – 6 780 = 20 000
29 000 x 2 = 58 000
46 000 + 14 000 = 60 000
41 450 + 8 550 = 50 000
36 000 : 4 = 9 000
Đặt tính rồi tính.
74 181 + 4 728 48 086 – 22 248
13 073 x 3 15 832 : 4
Phương pháp giải:
Đặt tính rồi tính theo các quy tắc đã học.
Lời giải chi tiết:
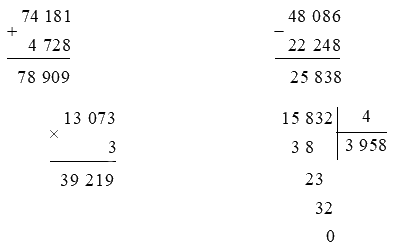
Tính giá trị của biểu thức:
a) 2 019 + m : 2 với m = 382; m = 2 020.
b) n x 3 + 5 190 với n = 106; n = 2 010.
c) (2 315 + p) : 5 – 565 với p = 510; p = 715.
Phương pháp giải:
Thay giá trị của chữ vào biểu thức rồi tính giá trị biểu thức đó.
Lời giải chi tiết:
a) Nếu m = 382 thì 2 019 + m : 2 = 2 019 + 382 : 2 = 2 019 + 191 = 2 210.
Nếu m = 2 020 thì 2 019 + m : 2 = 2 019 + 2 020 : 2 = 2 019 + 1 010 = 3 029.
b) Nếu n = 106 thì n x 3 + 5 190 = 106 x 3 + 5 190 = 318 + 5 190 = 5 508.
Nếu n = 2 010 thì n x 3 + 5 190 = 2 010 x 3 + 5 190 = 6 030 + 5 190 = 11 220.
c) Nếu p = 510 thì (2 315 + p) : 5 – 565 = (2 315 + 510) : 5 – 565
= 2 820 : 5 – 565
= 565 – 565 = 0.
Nếu p = 715 thì (2 315 + p) : 5 = (2 315 + 715) : 5 – 565
= 3 030 : 5 – 565
= 606 – 565 = 41.
Phần A: Tái hiện, củng cố trong bài tập phát triển năng lực Toán 4 trang 2, 3 tập trung vào việc giúp học sinh ôn lại kiến thức đã học về các phép tính cơ bản, đặc biệt là phép cộng, trừ, nhân, chia trong phạm vi 1000. Đồng thời, phần này cũng rèn luyện khả năng giải quyết các bài toán có liên quan đến thực tế cuộc sống.
Để giải các bài tập trong phần A: Tái hiện, củng cố trang 2, 3, học sinh cần nắm vững các kiến thức cơ bản về các phép tính cộng, trừ, nhân, chia. Đồng thời, học sinh cũng cần rèn luyện kỹ năng đọc hiểu đề bài, xác định đúng yêu cầu của bài toán và lựa chọn phương pháp giải phù hợp.
Khi giải các bài tập về phép cộng, trừ, học sinh cần thực hiện các bước sau:
Khi giải các bài tập về phép nhân, chia, học sinh cần thực hiện các bước sau:
Khi giải các bài toán thực tế, học sinh cần thực hiện các bước sau:
Ví dụ 1: Tính 345 + 234 = ?
Giải: 345 + 234 = 579
Ví dụ 2: Tính 678 - 456 = ?
Giải: 678 - 456 = 222
Ví dụ 3: Tính 123 x 4 = ?
Giải: 123 x 4 = 492
Ví dụ 4: Tính 567 : 3 = ?
Giải: 567 : 3 = 189
Việc ôn tập thường xuyên là rất quan trọng để giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Thông qua việc ôn tập, học sinh có thể nắm vững các khái niệm, định nghĩa và công thức toán học, đồng thời có thể áp dụng chúng vào việc giải quyết các bài toán thực tế.
Giaitoan.edu.vn hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh lớp 4 sẽ tự tin hơn trong việc giải các bài tập Toán 4 phần A: Tái hiện, củng cố trang 2, 3. Chúc các em học tập tốt!