Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong phần B, trang 15 sách Bài tập phát triển năng lực Toán 4 tập 2. Chúng tôi giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán một cách hiệu quả.
Giaitoan.edu.vn là địa chỉ tin cậy dành cho các em học sinh và phụ huynh tìm kiếm tài liệu học tập toán học chất lượng.
Viết chữ số thích hợp vào chỗ chấm và trả lời câu hỏi (nếu có):
Viết chữ số thích hợp vào ô trống và trả lời câu hỏi (nếu có):
a) 456............. chia hết cho 5 nhưng không chia hết cho 2.
b) 456............. chia hết cho 5 và chia hết cho 2.
Số vừa tìm được có chia hết cho 3 không?
c) 456............. chia hết cho 9.
Số vừa tìm được có chia hết cho 2 và 3 không?
Phương pháp giải:
- Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2.
- Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.
- Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.
- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
- Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
Lời giải chi tiết:
a) 4565 chia hết cho 5 nhưng không chia hết cho 2.
b) 4560 chia hết cho 5 và chia hết cho 2.
Số 4560 có tổng các chữ số là 15 chia hết cho 3 nên số 4560 chia hết cho 3.
c) 4563 chia hết cho 9.
Số 4563 có chữ số tận cùng là 3 nên không chia hết cho 2.
Số 4563 có tổng các chữ số là 18 chia hết cho 3 nên số 4563 chia hết cho 3.
Cho các phân số: \(\frac{{16}}{{32}};\frac{3}{4};\frac{8}{{20}};\frac{{54}}{{63}};\frac{9}{{45}}\). Hãy viết các phân số:
a) Bé hơn \(\frac{1}{2}{\text{. }}\)
b) Lớn hơn \(\frac{1}{2}{\text{. }}\)
Phương pháp giải:
So sánh các phân số bằng cách quy đồng mẫu số hoặc rút gọn phân số rồi đưa ra kết luận.
Lời giải chi tiết:
a) Các phân số bé hơn \(\frac{1}{2}\) là \(:\frac{8}{{20}};\frac{9}{{45}}.\)
b) Các phân số lớn hơn \(\frac{1}{2}\) là \(:\frac{3}{4};\frac{{54}}{{63}}.\)
Tính:
\({\text{a) }}\frac{{16}}{{32}} + 9 = ....................{\text{ }}\)
\(6 + \frac{{100}}{{300}} = ...................\)
\({\text{b) }}\frac{{1000}}{{10000}} + 8 = ....................{\text{ }}\)
\(\frac{{100}}{{500000}} + 10 = ....................\)
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản.
- Ta có thể viết các số tự nhiên dưới dạng phân số có mẫu số là 1, sau đó thực hiện phép cộng hai phân số như thông thường.
Lời giải chi tiết:
\({\text{a) }}\frac{{16}}{{32}} + 9 = \frac{1}{2} + 9 = \frac{1}{2}{\text{ + }}\frac{{18}}{2}{\text{ = }}\frac{{19}}{2}\)
\(6 + \frac{{100}}{{300}} = \frac{{18}}{3}{\text{ + }}\frac{1}{3}{\text{ = }}\frac{{19}}{3}\)
\({\text{b) }}\frac{{1000}}{{10000}} + 8 = \frac{1}{{10}}{\text{ + }}\frac{{80}}{{10}}{\text{ = }}\frac{{81}}{{10}}{\text{ }}\)
\(\frac{{100}}{{500000}} + 10 = \frac{1}{{5000}}{\text{ + }}\frac{{50000}}{{5000}}{\text{ = }}\frac{{50001}}{{5000}}{\text{ }}\)

Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản.
- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
Lời giải chi tiết:
\({\text{a) }}\frac{{36}}{{45}} + \frac{4}{{25}} = \frac{4}{5}{\text{ + }}\frac{4}{{25}} = \frac{{20}}{{25}}{\text{ + }}\frac{4}{{25}} = \frac{{24}}{{25}}\)
\(\frac{3}{{24}} + \frac{{12}}{{60}} = \frac{1}{8} + \frac{1}{5} = \frac{5}{{40}}{\text{ + }}\frac{8}{{40}}{\text{ = }}\frac{{13}}{{40}}{\text{ }}\)
\({\text{b) }}\frac{{14}}{{35}} + \frac{{36}}{{63}} = \frac{2}{5}{\text{ + }}\frac{4}{7}{\text{ = }}\frac{{14}}{{35}}{\text{ + }}\frac{{20}}{{35}}{\text{ = }}\frac{{34}}{{35}}{\text{ }}\)
\(\frac{3}{{21}} + \frac{{27}}{{15}} = \frac{1}{7}{\text{ + }}\frac{9}{5}{\text{ = }}\frac{5}{{35}}{\text{ + }}\frac{{63}}{{35}}{\text{ = }}\frac{{68}}{{35}}{\text{ }}\)
Đúng ghi Đ, sai ghi S:
\({\text{a) }}\frac{3}{{16}} + \frac{5}{{16}} = \frac{{3 + 5}}{{16}} = \frac{1}{2}\)
\({\text{b) }}\frac{{17}}{{28}} + \frac{5}{{28}} = \frac{{17 + 5}}{{28}} = \frac{{22}}{{28}}{\text{ }}\)
\({\text{c) }}\frac{{15}}{{27}} + \frac{2}{9} = \frac{5}{9} + \frac{2}{9} = \frac{{5 + 2}}{9} = \frac{7}{9}{\text{ }}\)
\({\text{d) }}\frac{{25}}{{26}} + \frac{1}{6} = \frac{{25 + 1}}{{26}} = \frac{{26}}{{26}}{\text{ }}\)
Phương pháp giải:
- Muốn cộng hai phân số cũng mẫu số ta cộng hai tử số với nhau và giữ nguyên mẫu số
- Muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số hai phân số rồi cộng hai phân số với nhau.
Lời giải chi tiết:

Viết vào chỗ trống cho thích hợp:
\({\text{a) }}\frac{3}{{20}} + \frac{9}{{20}} + \frac{1}{4} = \left( {\frac{3}{{20}} + \frac{9}{{20}}} \right) + .... = \frac{3}{{20}} + \left( {.... + \frac{1}{4}} \right).\)
\({\text{b) }}\frac{1}{2} + \frac{4}{9} + \frac{1}{{18}} = \left( {\frac{1}{2} + \frac{4}{9}} \right) + .... = \frac{1}{2} + \left( {.... + \frac{1}{{18}}} \right).\)
Phương pháp giải:
Áp dụng tính chất kết hợp của phép cộng: (a + b) + c = a + (b + c)
Lời giải chi tiết:
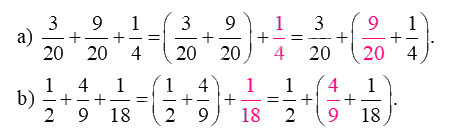
Thỏ và Rùa chạy thi:


Trả lời các câu hỏi sau:
a) Sau giờ đầu ai chạy được xa hơn?
b) Sau hai giờ ai chạy được xa hơn?
Phương pháp giải:
a) So sánh hai phân số $\frac{1}{2}$ và $\frac{1}{4}$ để trả lời câu hỏi đề bài.
b) Tính quãng đường thỏ chạy được sau 2 giờ, tính quãng đường rùa chạy được sau 2 giờ
So sánh kết quả tìm được.
Lời giải chi tiết:
a) Ta có: \(\frac{1}{2} = \frac{2}{4} > \frac{1}{4}\). Vậy sau giờ đầu Thỏ chạy được xa hơn.
b) Sau hai giờ rùa chạy được quãng đường là $\frac{1}{4} + \frac{2}{5} = \frac{{13}}{{20}}$ (quãng đường)
Sau hai giờ thỏ chạy được quãng đường là: $\frac{1}{2} + \frac{3}{{10}} = \frac{4}{5} = \frac{{16}}{{20}}$ (quãng đường)
Cho các phân số: \(\frac{{16}}{{32}};\frac{3}{4};\frac{8}{{20}};\frac{{54}}{{63}};\frac{9}{{45}}\). Hãy viết các phân số:
a) Bé hơn \(\frac{1}{2}{\text{. }}\)
b) Lớn hơn \(\frac{1}{2}{\text{. }}\)
Phương pháp giải:
So sánh các phân số bằng cách quy đồng mẫu số hoặc rút gọn phân số rồi đưa ra kết luận.
Lời giải chi tiết:
a) Các phân số bé hơn \(\frac{1}{2}\) là \(:\frac{8}{{20}};\frac{9}{{45}}.\)
b) Các phân số lớn hơn \(\frac{1}{2}\) là \(:\frac{3}{4};\frac{{54}}{{63}}.\)
Viết chữ số thích hợp vào ô trống và trả lời câu hỏi (nếu có):
a) 456............. chia hết cho 5 nhưng không chia hết cho 2.
b) 456............. chia hết cho 5 và chia hết cho 2.
Số vừa tìm được có chia hết cho 3 không?
c) 456............. chia hết cho 9.
Số vừa tìm được có chia hết cho 2 và 3 không?
Phương pháp giải:
- Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2.
- Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.
- Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.
- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
- Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
Lời giải chi tiết:
a) 4565 chia hết cho 5 nhưng không chia hết cho 2.
b) 4560 chia hết cho 5 và chia hết cho 2.
Số 4560 có tổng các chữ số là 15 chia hết cho 3 nên số 4560 chia hết cho 3.
c) 4563 chia hết cho 9.
Số 4563 có chữ số tận cùng là 3 nên không chia hết cho 2.
Số 4563 có tổng các chữ số là 18 chia hết cho 3 nên số 4563 chia hết cho 3.
Đúng ghi Đ, sai ghi S:
\({\text{a) }}\frac{3}{{16}} + \frac{5}{{16}} = \frac{{3 + 5}}{{16}} = \frac{1}{2}\)
\({\text{b) }}\frac{{17}}{{28}} + \frac{5}{{28}} = \frac{{17 + 5}}{{28}} = \frac{{22}}{{28}}{\text{ }}\)
\({\text{c) }}\frac{{15}}{{27}} + \frac{2}{9} = \frac{5}{9} + \frac{2}{9} = \frac{{5 + 2}}{9} = \frac{7}{9}{\text{ }}\)
\({\text{d) }}\frac{{25}}{{26}} + \frac{1}{6} = \frac{{25 + 1}}{{26}} = \frac{{26}}{{26}}{\text{ }}\)
Phương pháp giải:
- Muốn cộng hai phân số cũng mẫu số ta cộng hai tử số với nhau và giữ nguyên mẫu số
- Muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số hai phân số rồi cộng hai phân số với nhau.
Lời giải chi tiết:


Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản.
- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
Lời giải chi tiết:
\({\text{a) }}\frac{{36}}{{45}} + \frac{4}{{25}} = \frac{4}{5}{\text{ + }}\frac{4}{{25}} = \frac{{20}}{{25}}{\text{ + }}\frac{4}{{25}} = \frac{{24}}{{25}}\)
\(\frac{3}{{24}} + \frac{{12}}{{60}} = \frac{1}{8} + \frac{1}{5} = \frac{5}{{40}}{\text{ + }}\frac{8}{{40}}{\text{ = }}\frac{{13}}{{40}}{\text{ }}\)
\({\text{b) }}\frac{{14}}{{35}} + \frac{{36}}{{63}} = \frac{2}{5}{\text{ + }}\frac{4}{7}{\text{ = }}\frac{{14}}{{35}}{\text{ + }}\frac{{20}}{{35}}{\text{ = }}\frac{{34}}{{35}}{\text{ }}\)
\(\frac{3}{{21}} + \frac{{27}}{{15}} = \frac{1}{7}{\text{ + }}\frac{9}{5}{\text{ = }}\frac{5}{{35}}{\text{ + }}\frac{{63}}{{35}}{\text{ = }}\frac{{68}}{{35}}{\text{ }}\)
Tính:
\({\text{a) }}\frac{{16}}{{32}} + 9 = ....................{\text{ }}\)
\(6 + \frac{{100}}{{300}} = ...................\)
\({\text{b) }}\frac{{1000}}{{10000}} + 8 = ....................{\text{ }}\)
\(\frac{{100}}{{500000}} + 10 = ....................\)
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản.
- Ta có thể viết các số tự nhiên dưới dạng phân số có mẫu số là 1, sau đó thực hiện phép cộng hai phân số như thông thường.
Lời giải chi tiết:
\({\text{a) }}\frac{{16}}{{32}} + 9 = \frac{1}{2} + 9 = \frac{1}{2}{\text{ + }}\frac{{18}}{2}{\text{ = }}\frac{{19}}{2}\)
\(6 + \frac{{100}}{{300}} = \frac{{18}}{3}{\text{ + }}\frac{1}{3}{\text{ = }}\frac{{19}}{3}\)
\({\text{b) }}\frac{{1000}}{{10000}} + 8 = \frac{1}{{10}}{\text{ + }}\frac{{80}}{{10}}{\text{ = }}\frac{{81}}{{10}}{\text{ }}\)
\(\frac{{100}}{{500000}} + 10 = \frac{1}{{5000}}{\text{ + }}\frac{{50000}}{{5000}}{\text{ = }}\frac{{50001}}{{5000}}{\text{ }}\)
Viết vào chỗ trống cho thích hợp:
\({\text{a) }}\frac{3}{{20}} + \frac{9}{{20}} + \frac{1}{4} = \left( {\frac{3}{{20}} + \frac{9}{{20}}} \right) + .... = \frac{3}{{20}} + \left( {.... + \frac{1}{4}} \right).\)
\({\text{b) }}\frac{1}{2} + \frac{4}{9} + \frac{1}{{18}} = \left( {\frac{1}{2} + \frac{4}{9}} \right) + .... = \frac{1}{2} + \left( {.... + \frac{1}{{18}}} \right).\)
Phương pháp giải:
Áp dụng tính chất kết hợp của phép cộng: (a + b) + c = a + (b + c)
Lời giải chi tiết:
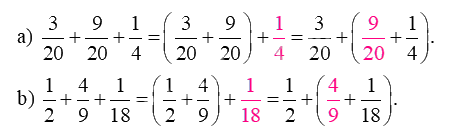
Thỏ và Rùa chạy thi:


Trả lời các câu hỏi sau:
a) Sau giờ đầu ai chạy được xa hơn?
b) Sau hai giờ ai chạy được xa hơn?
Phương pháp giải:
a) So sánh hai phân số $\frac{1}{2}$ và $\frac{1}{4}$ để trả lời câu hỏi đề bài.
b) Tính quãng đường thỏ chạy được sau 2 giờ, tính quãng đường rùa chạy được sau 2 giờ
So sánh kết quả tìm được.
Lời giải chi tiết:
a) Ta có: \(\frac{1}{2} = \frac{2}{4} > \frac{1}{4}\). Vậy sau giờ đầu Thỏ chạy được xa hơn.
b) Sau hai giờ rùa chạy được quãng đường là $\frac{1}{4} + \frac{2}{5} = \frac{{13}}{{20}}$ (quãng đường)
Sau hai giờ thỏ chạy được quãng đường là: $\frac{1}{2} + \frac{3}{{10}} = \frac{4}{5} = \frac{{16}}{{20}}$ (quãng đường)
Phần B của bài tập phát triển năng lực Toán 4 tập 2, trang 15, tập trung vào việc củng cố kiến thức về các phép tính với số có nhiều chữ số, đặc biệt là phép cộng và trừ. Các bài tập được thiết kế để học sinh vận dụng kiến thức đã học vào giải quyết các bài toán thực tế, giúp các em hiểu rõ hơn về ứng dụng của toán học trong cuộc sống.
Phần này sẽ đi sâu vào giải chi tiết từng bài tập trong phần B, trang 15. Chúng ta sẽ cùng nhau phân tích đề bài, xác định yêu cầu và tìm ra phương pháp giải phù hợp.
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng và trừ nhẩm với các số có nhiều chữ số. Để giải bài này, học sinh cần nắm vững các quy tắc cộng và trừ, đồng thời rèn luyện khả năng tính toán nhanh và chính xác.
Bài 2 yêu cầu học sinh thực hiện các phép tính cộng và trừ bằng cột dọc. Đây là phương pháp giúp học sinh dễ dàng kiểm soát các chữ số và tránh sai sót trong quá trình tính toán.
Bài 3 là một bài toán có lời văn, yêu cầu học sinh đọc kỹ đề bài, xác định các dữ kiện và yêu cầu, sau đó lập kế hoạch giải và thực hiện các phép tính để tìm ra đáp án.
Ví dụ: Một cửa hàng có 235 kg gạo. Buổi sáng cửa hàng bán được 120 kg gạo, buổi chiều bán được 85 kg gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Hướng dẫn:
Để giải các bài tập toán 4 tập 2 một cách hiệu quả, học sinh cần:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể tự giải thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online.
Giải phần B. Kết nối trang 15 Toán 4 Tập 2 là một bước quan trọng trong quá trình học toán của học sinh. Hy vọng với hướng dẫn chi tiết và các mẹo giải toán hiệu quả, các em sẽ tự tin hơn khi đối mặt với các bài tập toán học.
| Bài tập | Hướng dẫn |
|---|---|
| Bài 1 | Tính nhẩm nhanh và chính xác. |
| Bài 2 | Sử dụng cột dọc để tránh sai sót. |
| Bài 3 | Đọc kỹ đề, xác định dữ kiện và lập kế hoạch giải. |
| Chúc các em học tốt! | |