Chào mừng các em học sinh đến với bài giải chi tiết phần A. Tái hiện, củng cố trang 20 trong sách Bài tập phát triển năng lực Toán 4 tập 2. Bài học này giúp các em ôn lại kiến thức đã học và rèn luyện kỹ năng giải toán một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Khoanh vào chữ đặt trước câu trả lời đúng ...
Tính:
\({\text{a) }}\frac{5}{6} \times \frac{1}{{10}} = ....................{\text{ }}\)
\(\frac{3}{8} \times \frac{4}{9} = ....................{\text{ }}\)
\({\text{b) }}\frac{7}{9} \times \frac{9}{7} = ....................{\text{ }}\)
\(\frac{{11}}{{15}} \times \frac{5}{{22}} = ....................{\text{ }}\)
Phương pháp giải:
Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số
Lời giải chi tiết:
\({\text{a) }}\frac{5}{6} \times \frac{1}{{10}} = \frac{{5 \times 1}}{{6 \times 10}}{\text{ = }}\frac{5}{{60}}{\text{ = }}\frac{1}{{12}}{\text{ }}\)
\(\frac{3}{8} \times \frac{4}{9} = \frac{{3 \times 4}}{{8 \times 9}}{\text{ = }}\frac{{12}}{{72}}{\text{ = }}\frac{1}{6}{\text{ }}\)
\({\text{b) }}\frac{7}{9} \times \frac{9}{7} = \frac{{7 \times 9}}{{9 \times 7}}{\text{ = 1 }}\)
\(\frac{{11}}{{15}} \times \frac{5}{{22}} = \frac{{11 \times 5}}{{15 \times 22}}{\text{ = }}\frac{{55}}{{330}}{\text{ = }}\frac{1}{6}{\text{ }}\)
Tính:
\({\text{a) }}\frac{1}{2} \times 3 = ....................{\text{ }}\)
\(\frac{2}{3} \times 4 = ....................{\text{ }}\)
\({\text{b) }}12 \times \frac{1}{5} = ....................{\text{ }}\)
\(11 \times \frac{2}{9} = ....................{\text{ }}\)
Phương pháp giải:
Muốn nhân một phân số với một số tự nhiên ta lấy tử số nhân với số tự nhiên đó và giữ nguyên mẫu số
Lời giải chi tiết:
\({\text{a) }}\frac{1}{2} \times 3 = \frac{{1 \times 3}}{2}{\text{ = }}\frac{3}{2}{\text{ }}\)
\(\frac{2}{3} \times 4 = \frac{{2 \times 4}}{3} = \frac{8}{3}\)
\({\text{b) }}12 \times \frac{1}{5} = \frac{{12 \times 1}}{5}{\text{ = }}\frac{{12}}{5}{\text{ }}\)
\(11 \times \frac{2}{9} = \frac{{11 \times 2}}{9} = \frac{{22}}{9}{\text{ }}\)
Tính:
\({\text{a) }}\frac{5}{2}:\frac{3}{7} = ....................{\text{ }}\)
\(\frac{1}{2}:\frac{1}{4} = ....................{\text{ }}\)
\({\text{b) }}\frac{3}{5}:\frac{1}{5} = ....................{\text{ }}\)
\(\frac{5}{9}:\frac{4}{3} = ....................{\text{ }}\)
Phương pháp giải:
Để thực hiện phép chia hai phân số, ta làm như sau: Lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:
\({\text{a) }}\frac{5}{2}:\frac{3}{7} = \frac{5}{2} \times \frac{7}{3} = \frac{{35}}{6}{\text{ }}\)
\(\frac{1}{2}:\frac{1}{4} = \frac{1}{2} \times \frac{4}{1} = 2{\text{ }}\)
\({\text{b) }}\frac{3}{5}:\frac{1}{5} = \frac{3}{5} \times \frac{5}{1} = 3{\text{ }}\)
\(\frac{5}{9}:\frac{4}{3} = \frac{5}{9} \times \frac{3}{4}{\text{ = }}\frac{5}{{12}}{\text{ }}\)
Khoanh vào chữ đặt trước câu trả lời đúng:
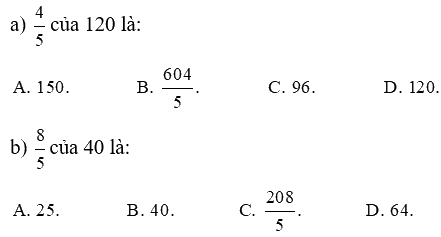
Phương pháp giải:
Muốn tìm phân số của một số ta lấy số đã cho nhân với phân số đó.
Lời giải chi tiết:
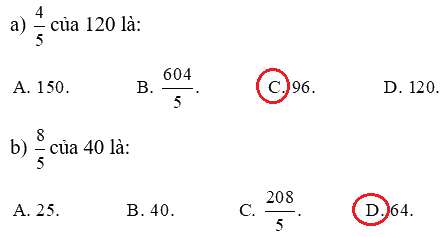
Khoanh vào chữ đặt trước câu trả lời đúng:

Phương pháp giải:
a) Áp dụng tính chất giao hoán của phép nhân: a x b = b x a.
b) Áp dụng tính chất kết hợp của phép nhân: (a x b) x c = a x (b x c).
c) Áp dụng công thức (a + b) x c = a x c + b x c.
Lời giải chi tiết:

Tính:
\({\text{a) }}\frac{5}{6} \times \frac{1}{{10}} = ....................{\text{ }}\)
\(\frac{3}{8} \times \frac{4}{9} = ....................{\text{ }}\)
\({\text{b) }}\frac{7}{9} \times \frac{9}{7} = ....................{\text{ }}\)
\(\frac{{11}}{{15}} \times \frac{5}{{22}} = ....................{\text{ }}\)
Phương pháp giải:
Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số
Lời giải chi tiết:
\({\text{a) }}\frac{5}{6} \times \frac{1}{{10}} = \frac{{5 \times 1}}{{6 \times 10}}{\text{ = }}\frac{5}{{60}}{\text{ = }}\frac{1}{{12}}{\text{ }}\)
\(\frac{3}{8} \times \frac{4}{9} = \frac{{3 \times 4}}{{8 \times 9}}{\text{ = }}\frac{{12}}{{72}}{\text{ = }}\frac{1}{6}{\text{ }}\)
\({\text{b) }}\frac{7}{9} \times \frac{9}{7} = \frac{{7 \times 9}}{{9 \times 7}}{\text{ = 1 }}\)
\(\frac{{11}}{{15}} \times \frac{5}{{22}} = \frac{{11 \times 5}}{{15 \times 22}}{\text{ = }}\frac{{55}}{{330}}{\text{ = }}\frac{1}{6}{\text{ }}\)
Tính:
\({\text{a) }}\frac{1}{2} \times 3 = ....................{\text{ }}\)
\(\frac{2}{3} \times 4 = ....................{\text{ }}\)
\({\text{b) }}12 \times \frac{1}{5} = ....................{\text{ }}\)
\(11 \times \frac{2}{9} = ....................{\text{ }}\)
Phương pháp giải:
Muốn nhân một phân số với một số tự nhiên ta lấy tử số nhân với số tự nhiên đó và giữ nguyên mẫu số
Lời giải chi tiết:
\({\text{a) }}\frac{1}{2} \times 3 = \frac{{1 \times 3}}{2}{\text{ = }}\frac{3}{2}{\text{ }}\)
\(\frac{2}{3} \times 4 = \frac{{2 \times 4}}{3} = \frac{8}{3}\)
\({\text{b) }}12 \times \frac{1}{5} = \frac{{12 \times 1}}{5}{\text{ = }}\frac{{12}}{5}{\text{ }}\)
\(11 \times \frac{2}{9} = \frac{{11 \times 2}}{9} = \frac{{22}}{9}{\text{ }}\)
Khoanh vào chữ đặt trước câu trả lời đúng:

Phương pháp giải:
a) Áp dụng tính chất giao hoán của phép nhân: a x b = b x a.
b) Áp dụng tính chất kết hợp của phép nhân: (a x b) x c = a x (b x c).
c) Áp dụng công thức (a + b) x c = a x c + b x c.
Lời giải chi tiết:

Khoanh vào chữ đặt trước câu trả lời đúng:
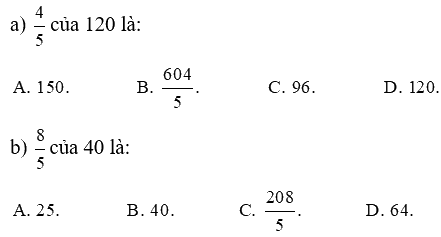
Phương pháp giải:
Muốn tìm phân số của một số ta lấy số đã cho nhân với phân số đó.
Lời giải chi tiết:
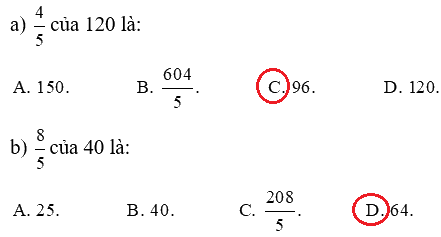
Tính:
\({\text{a) }}\frac{5}{2}:\frac{3}{7} = ....................{\text{ }}\)
\(\frac{1}{2}:\frac{1}{4} = ....................{\text{ }}\)
\({\text{b) }}\frac{3}{5}:\frac{1}{5} = ....................{\text{ }}\)
\(\frac{5}{9}:\frac{4}{3} = ....................{\text{ }}\)
Phương pháp giải:
Để thực hiện phép chia hai phân số, ta làm như sau: Lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:
\({\text{a) }}\frac{5}{2}:\frac{3}{7} = \frac{5}{2} \times \frac{7}{3} = \frac{{35}}{6}{\text{ }}\)
\(\frac{1}{2}:\frac{1}{4} = \frac{1}{2} \times \frac{4}{1} = 2{\text{ }}\)
\({\text{b) }}\frac{3}{5}:\frac{1}{5} = \frac{3}{5} \times \frac{5}{1} = 3{\text{ }}\)
\(\frac{5}{9}:\frac{4}{3} = \frac{5}{9} \times \frac{3}{4}{\text{ = }}\frac{5}{{12}}{\text{ }}\)
Phần A. Tái hiện, củng cố trang 20 trong sách Bài tập phát triển năng lực Toán 4 tập 2 tập trung vào việc giúp học sinh củng cố kiến thức về các phép tính cơ bản, đặc biệt là phép cộng, trừ, nhân, chia các số có nhiều chữ số. Các bài tập trong phần này thường được trình bày dưới dạng các bài toán thực tế, đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết.
Bài 1 thường yêu cầu học sinh tính toán số lượng các đối tượng trong một tình huống cụ thể. Ví dụ, bài toán có thể yêu cầu tính tổng số học sinh trong một lớp, hoặc số lượng sản phẩm được sản xuất trong một ngày. Để giải bài toán này, học sinh cần xác định rõ các thông tin quan trọng trong đề bài, sau đó sử dụng các phép tính cộng, trừ, nhân, chia để tìm ra đáp án.
Bài 2 thường yêu cầu học sinh xác định giá trị của một số lượng lớn các đối tượng. Ví dụ, bài toán có thể yêu cầu tính tổng giá trị của một số lượng sản phẩm, hoặc tổng số tiền thu được từ việc bán hàng. Để giải bài toán này, học sinh cần nhân số lượng đối tượng với giá trị của mỗi đối tượng, sau đó cộng các kết quả lại với nhau.
Bài 3 thường yêu cầu học sinh tính toán thời gian cần thiết để hoàn thành một công việc. Ví dụ, bài toán có thể yêu cầu tính thời gian đi từ nhà đến trường, hoặc thời gian cần thiết để hoàn thành một bài tập. Để giải bài toán này, học sinh cần sử dụng các phép tính cộng, trừ, nhân, chia để tính toán thời gian.
Bài 4 thường yêu cầu học sinh thực hiện các phép đo lường và tính toán các đại lượng liên quan đến đo lường. Ví dụ, bài toán có thể yêu cầu tính chiều dài của một hình chữ nhật, hoặc diện tích của một hình vuông. Để giải bài toán này, học sinh cần sử dụng các công thức đo lường và các phép tính cộng, trừ, nhân, chia.
Bài toán: Một cửa hàng có 250 kg gạo tẻ và 180 kg gạo nếp. Hỏi cửa hàng có tất cả bao nhiêu ki-lô-gam gạo?
Giải:
Tổng số gạo cửa hàng có là: 250 + 180 = 430 (kg)
Đáp số: Cửa hàng có tất cả 430 kg gạo.
Để củng cố kiến thức và kỹ năng giải toán, các em có thể luyện tập thêm các bài tập tương tự trong sách Bài tập phát triển năng lực Toán 4 tập 2, hoặc tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Phần A. Tái hiện, củng cố trang 20 Toán 4 tập 2 là một phần quan trọng trong chương trình học Toán 4. Việc nắm vững kiến thức và kỹ năng giải toán trong phần này sẽ giúp các em học tốt môn Toán và đạt kết quả cao trong các kỳ thi.