Bài tập phát triển năng lực Toán 4 tập 2 trang 15 phần A yêu cầu học sinh tái hiện và củng cố kiến thức đã học về các phép tính cơ bản và ứng dụng vào giải quyết các bài toán thực tế. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải bài tập đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức.
Điền dấu (>; <; =) thích hợp vào chỗ trống
Điền dấu (>; <; =) thích hợp vào chỗ trống:
\({\text{a) }}\frac{4}{5}{\text{ }}....{\text{ }}\frac{2}{5};\frac{8}{{13}}{\text{ }}....{\text{ }}\frac{8}{{27}};\frac{{52}}{{49}}{\text{ }}....{\text{ }}1\)
\({\text{b) }}\frac{7}{9}{\text{ }}....{\text{ }}\frac{5}{3};\frac{1}{4}{\text{ }}....{\text{ }}\frac{6}{{16}};1{\text{ }}....{\text{ }}\frac{{27}}{{28}}\)
Phương pháp giải:
- So sánh hai phân số cùng mẫu số: Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
- So sánh hai phân số cùng tử số: Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
- So sánh phân số với 1:
+ Nếu tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.
+ Nếu tử số bé hơn mẫu số thì phân số đó bé hơn 1.
Lời giải chi tiết:
\({\text{a) }}\frac{4}{5} > \frac{2}{5};\frac{8}{{13}} > \frac{8}{{27}};\frac{{52}}{{49}} > 1\)
\({\text{b) }}\frac{7}{9} < \frac{5}{3};\frac{1}{4}{\text{ < }}\frac{6}{{16}};1 > \frac{{27}}{{28}}\)
Tính:
\({\text{a) }}\frac{2}{6}{\text{ + }}\frac{4}{6}{\text{ = }}.....................\)
\({\text{b) }}\frac{2}{9} + \frac{3}{9} = .....................{\text{ }}\)
\({\text{c) }}\frac{3}{4} + \frac{5}{4} = .....................\)
Phương pháp giải:
Muốn cộng hai phân số cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.
Lời giải chi tiết:
\({\text{a) }}\frac{2}{6} + \frac{4}{6} = \frac{{2 + 4}}{6} = \frac{6}{6} = 1\)
\({\text{b) }}\frac{2}{9} + \frac{3}{9} = \frac{{2 + 3}}{9} = \frac{5}{9}\)
\({\text{c) }}\frac{3}{4} + \frac{5}{4} = \frac{{3 + 5}}{4} = \frac{8}{4} = 2{\text{ }}\)
Tính:
\({\text{a) }}\frac{2}{3}{\text{ + }}\frac{1}{5}{\text{ = }}.....................\)
\({\text{b) }}\frac{3}{7} + \frac{9}{{14}} = .....................{\text{ }}\)
\({\text{c) }}\frac{5}{{12}} + \frac{3}{4} = .....................{\text{ }}\)
Phương pháp giải:
Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
Lời giải chi tiết:
\({\text{a) }}\frac{2}{3}{\text{ + }}\frac{1}{5}{\text{ = }}\frac{{10}}{{15}}{\text{ + }}\frac{3}{{15}}{\text{ = }}\frac{{13}}{{15}}\)
\({\text{b) }}\frac{3}{7} + \frac{9}{{14}} = \frac{6}{{14}}{\text{ + }}\frac{9}{{14}}{\text{ = }}\frac{{15}}{{14}}\)
\({\text{c) }}\frac{5}{{12}} + \frac{3}{4} = \frac{5}{{12}}{\text{ + }}\frac{9}{{12}}{\text{ = }}\frac{{14}}{{12}}{\text{ = }}\frac{7}{6}{\text{ }}\)
Phân số thích hợp điền vào chỗ trống để \(\frac{3}{5} + \frac{4}{5} = ........... + \frac{3}{5}\) là:
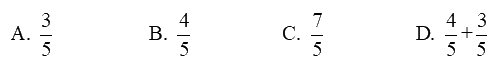
Phương pháp giải:
Áp dụng tính chất giao hoán: Khi ta đổi chỗ hai phân số trong một tổng thì tổng của chúng không thay đổi.
Lời giải chi tiết:
Ta có $\frac{3}{5} + \frac{4}{5} = \frac{4}{5} + \frac{3}{5}$
Vậy phân số cần điền vào chỗ chấm là $\frac{4}{5}$.
Chọn B.
Điền dấu (>; <; =) thích hợp vào chỗ trống:
\({\text{a) }}\frac{4}{5}{\text{ }}....{\text{ }}\frac{2}{5};\frac{8}{{13}}{\text{ }}....{\text{ }}\frac{8}{{27}};\frac{{52}}{{49}}{\text{ }}....{\text{ }}1\)
\({\text{b) }}\frac{7}{9}{\text{ }}....{\text{ }}\frac{5}{3};\frac{1}{4}{\text{ }}....{\text{ }}\frac{6}{{16}};1{\text{ }}....{\text{ }}\frac{{27}}{{28}}\)
Phương pháp giải:
- So sánh hai phân số cùng mẫu số: Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
- So sánh hai phân số cùng tử số: Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
- So sánh phân số với 1:
+ Nếu tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.
+ Nếu tử số bé hơn mẫu số thì phân số đó bé hơn 1.
Lời giải chi tiết:
\({\text{a) }}\frac{4}{5} > \frac{2}{5};\frac{8}{{13}} > \frac{8}{{27}};\frac{{52}}{{49}} > 1\)
\({\text{b) }}\frac{7}{9} < \frac{5}{3};\frac{1}{4}{\text{ < }}\frac{6}{{16}};1 > \frac{{27}}{{28}}\)
Tính:
\({\text{a) }}\frac{2}{6}{\text{ + }}\frac{4}{6}{\text{ = }}.....................\)
\({\text{b) }}\frac{2}{9} + \frac{3}{9} = .....................{\text{ }}\)
\({\text{c) }}\frac{3}{4} + \frac{5}{4} = .....................\)
Phương pháp giải:
Muốn cộng hai phân số cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.
Lời giải chi tiết:
\({\text{a) }}\frac{2}{6} + \frac{4}{6} = \frac{{2 + 4}}{6} = \frac{6}{6} = 1\)
\({\text{b) }}\frac{2}{9} + \frac{3}{9} = \frac{{2 + 3}}{9} = \frac{5}{9}\)
\({\text{c) }}\frac{3}{4} + \frac{5}{4} = \frac{{3 + 5}}{4} = \frac{8}{4} = 2{\text{ }}\)
Phân số thích hợp điền vào chỗ trống để \(\frac{3}{5} + \frac{4}{5} = ........... + \frac{3}{5}\) là:
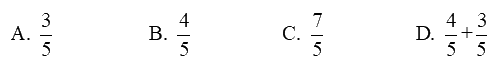
Phương pháp giải:
Áp dụng tính chất giao hoán: Khi ta đổi chỗ hai phân số trong một tổng thì tổng của chúng không thay đổi.
Lời giải chi tiết:
Ta có $\frac{3}{5} + \frac{4}{5} = \frac{4}{5} + \frac{3}{5}$
Vậy phân số cần điền vào chỗ chấm là $\frac{4}{5}$.
Chọn B.
Tính:
\({\text{a) }}\frac{2}{3}{\text{ + }}\frac{1}{5}{\text{ = }}.....................\)
\({\text{b) }}\frac{3}{7} + \frac{9}{{14}} = .....................{\text{ }}\)
\({\text{c) }}\frac{5}{{12}} + \frac{3}{4} = .....................{\text{ }}\)
Phương pháp giải:
Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
Lời giải chi tiết:
\({\text{a) }}\frac{2}{3}{\text{ + }}\frac{1}{5}{\text{ = }}\frac{{10}}{{15}}{\text{ + }}\frac{3}{{15}}{\text{ = }}\frac{{13}}{{15}}\)
\({\text{b) }}\frac{3}{7} + \frac{9}{{14}} = \frac{6}{{14}}{\text{ + }}\frac{9}{{14}}{\text{ = }}\frac{{15}}{{14}}\)
\({\text{c) }}\frac{5}{{12}} + \frac{3}{4} = \frac{5}{{12}}{\text{ + }}\frac{9}{{12}}{\text{ = }}\frac{{14}}{{12}}{\text{ = }}\frac{7}{6}{\text{ }}\)
Phần A của bài tập này tập trung vào việc củng cố các kiến thức cơ bản về cộng, trừ, nhân, chia các số tự nhiên, đồng thời rèn luyện kỹ năng giải toán có lời văn. Dưới đây là lời giải chi tiết cho từng bài tập:
Bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia một cách nhanh chóng và chính xác. Để làm tốt bài tập này, học sinh cần nắm vững bảng cửu chương và các quy tắc tính toán cơ bản.
Bài tập này yêu cầu học sinh đọc kỹ đề bài, xác định được các yếu tố quan trọng (số liệu, đơn vị, câu hỏi) và lựa chọn phép tính phù hợp để giải bài toán. Dưới đây là một ví dụ:
Đề bài: Một cửa hàng có 35 kg gạo. Buổi sáng cửa hàng bán được 12 kg gạo, buổi chiều bán được 15 kg gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Lời giải:
Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để điền vào chỗ trống các số hoặc phép tính thích hợp. Ví dụ:
5 x … = 30
… + 15 = 25
Để học tốt môn Toán 4, học sinh cần:
Việc giải các bài tập phát triển năng lực không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện các kỹ năng quan trọng như tư duy logic, khả năng giải quyết vấn đề và kỹ năng làm việc độc lập. Những kỹ năng này rất cần thiết cho sự thành công của học sinh trong học tập và cuộc sống.
| Phép tính | Ví dụ |
|---|---|
| Cộng | 2 + 3 = 5 |
| Trừ | 5 - 2 = 3 |
| Nhân | 2 x 3 = 6 |
| Chia | 6 : 2 = 3 |
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 4. Chúc các em học tốt!