Bài tập Giải Phần A. Tái hiện, củng cố trang 24 trong sách Bài tập phát triển năng lực Toán 4 là một phần quan trọng giúp học sinh củng cố kiến thức đã học về các phép tính và ứng dụng vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập, giúp học sinh tự tin hơn trong quá trình học tập.
Tìm x, biết a) x + 23 155 = 36 236. Tính giá trị của hai biểu thức m x n + p và (m + n) : p biết: m = 24; n = 8; p = 4.
Tìm x, biết:
a) x + 23155 = 36236
b) x – 71286 = 625437
c) 612794 – x = 150846
Phương pháp giải:
- Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
- Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
- Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
Lời giải chi tiết:
a) x + 23155 = 36236
x = 36236 – 23155
x = 13081
b) x – 71286 = 625437
x = 625437 + 71286
x = 696723
c) 612794 – x = 150846
x = 612794 – 150864
x = 461948
Viết giá trị của biểu thức vào ô trống:
m | n | m + n | m – n | m x n | m : n |
96 | 4 | ||||
78 | 3 | ||||
85 | 5 | ||||
40 | 8 |
Phương pháp giải:
Thay giá trị của chữ vào biểu thức rồi tính giá trị biểu thức đó.
Lời giải chi tiết:
m | n | m + n | m – n | m x n | m : n |
96 | 4 | 100 | 92 | 384 | 24 |
78 | 3 | 81 | 75 | 234 | 26 |
85 | 5 | 90 | 80 | 425 | 17 |
40 | 8 | 48 | 32 | 320 | 5 |
Tính giá trị của hai biểu thức m x n + p và (m + n) : p biết:
a) m = 24; n = 8; p = 4.
b) m = 102; n = 8; p = 5.
Phương pháp giải:
Thay giá trị của chữ vào biểu thức rồi tính giá trị biểu thức đó.
Lời giải chi tiết:
a) Nếu m = 24; n = 8; p = 4 thì m x n + p = 24 x 8 + 4 = 192 + 4 = 196.
Nếu m = 24; n = 8; p = 4 thì (m + n) : p = (24 + 8) : 4 = 32 : 4 = 8.
b)
Nếu m = 102; n = 8; p = 5 thì m x n + p = 102 x 8 + 5 = 816 + 5 = 821.
Nếu m = 102; n = 8; p = 5 thì (m + n) : p = (102 + 8) : 5 = 110 : 5 = 22.
Không thực hiện phép tính, hãy tìm x:
a) 23167 + x = 312 + 23167
b) (x + 23125) + 4507 = 245 + (23125 + 4507)
c) x + 34217 = 34217 + 56
d) (45145 + 982) + x = 45145 + (982 + 23)
Phương pháp giải:
Áp dụng tính chất giao hoán của phép cộng, em viết các số còn thiếu theo công thức a + b = b + a.
Lời giải chi tiết:
a) 23167 + x = 312 + 23167
Vậy x = 312
b) (x + 23125) + 4507 = 245 + (23125 + 4507)
Vậy x = 245
c) x + 34217 = 34217 + 56
Vậy x = 56
d) (45145 + 982) + x = 45145 + (982 + 23)
Vậy x = 23
Tính rồi thử lại:
361482 + 280725
292386 – 86429
Phương pháp giải:
- Đặt tính sao cho các chữ số cùng hàng thẳng cột với nhau.
- Tính theo thứ tự từ phải sang trái.
- Thử lại: Lấy tổng trừ đi một số hạng, nếu được kết quả bằng số hạng còn lại thì phép tính làm đúng; Lấy hiệu cộng với số trừ, nếu được kết quả bằng số bị trừ thì phép tính làm đúng.
Lời giải chi tiết:

Tính.
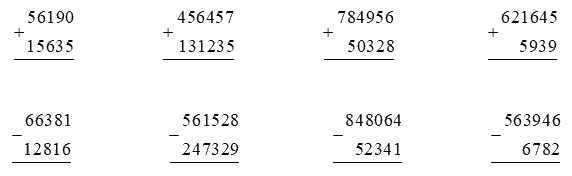
Phương pháp giải:
Cộng, trừ các chữ số thẳng cột lần lượt từ phải sang trái.
Lời giải chi tiết:

Tính.
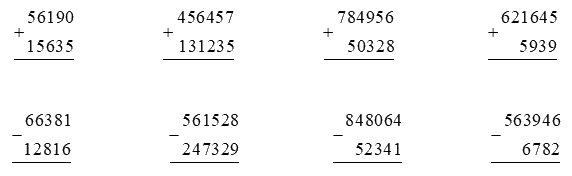
Phương pháp giải:
Cộng, trừ các chữ số thẳng cột lần lượt từ phải sang trái.
Lời giải chi tiết:

Viết giá trị của biểu thức vào ô trống:
m | n | m + n | m – n | m x n | m : n |
96 | 4 | ||||
78 | 3 | ||||
85 | 5 | ||||
40 | 8 |
Phương pháp giải:
Thay giá trị của chữ vào biểu thức rồi tính giá trị biểu thức đó.
Lời giải chi tiết:
m | n | m + n | m – n | m x n | m : n |
96 | 4 | 100 | 92 | 384 | 24 |
78 | 3 | 81 | 75 | 234 | 26 |
85 | 5 | 90 | 80 | 425 | 17 |
40 | 8 | 48 | 32 | 320 | 5 |
Tìm x, biết:
a) x + 23155 = 36236
b) x – 71286 = 625437
c) 612794 – x = 150846
Phương pháp giải:
- Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
- Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
- Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
Lời giải chi tiết:
a) x + 23155 = 36236
x = 36236 – 23155
x = 13081
b) x – 71286 = 625437
x = 625437 + 71286
x = 696723
c) 612794 – x = 150846
x = 612794 – 150864
x = 461948
Tính rồi thử lại:
361482 + 280725
292386 – 86429
Phương pháp giải:
- Đặt tính sao cho các chữ số cùng hàng thẳng cột với nhau.
- Tính theo thứ tự từ phải sang trái.
- Thử lại: Lấy tổng trừ đi một số hạng, nếu được kết quả bằng số hạng còn lại thì phép tính làm đúng; Lấy hiệu cộng với số trừ, nếu được kết quả bằng số bị trừ thì phép tính làm đúng.
Lời giải chi tiết:

Tính giá trị của hai biểu thức m x n + p và (m + n) : p biết:
a) m = 24; n = 8; p = 4.
b) m = 102; n = 8; p = 5.
Phương pháp giải:
Thay giá trị của chữ vào biểu thức rồi tính giá trị biểu thức đó.
Lời giải chi tiết:
a) Nếu m = 24; n = 8; p = 4 thì m x n + p = 24 x 8 + 4 = 192 + 4 = 196.
Nếu m = 24; n = 8; p = 4 thì (m + n) : p = (24 + 8) : 4 = 32 : 4 = 8.
b)
Nếu m = 102; n = 8; p = 5 thì m x n + p = 102 x 8 + 5 = 816 + 5 = 821.
Nếu m = 102; n = 8; p = 5 thì (m + n) : p = (102 + 8) : 5 = 110 : 5 = 22.
Không thực hiện phép tính, hãy tìm x:
a) 23167 + x = 312 + 23167
b) (x + 23125) + 4507 = 245 + (23125 + 4507)
c) x + 34217 = 34217 + 56
d) (45145 + 982) + x = 45145 + (982 + 23)
Phương pháp giải:
Áp dụng tính chất giao hoán của phép cộng, em viết các số còn thiếu theo công thức a + b = b + a.
Lời giải chi tiết:
a) 23167 + x = 312 + 23167
Vậy x = 312
b) (x + 23125) + 4507 = 245 + (23125 + 4507)
Vậy x = 245
c) x + 34217 = 34217 + 56
Vậy x = 56
d) (45145 + 982) + x = 45145 + (982 + 23)
Vậy x = 23
Phần A. Tái hiện, củng cố trang 24 trong sách Bài tập phát triển năng lực Toán 4 tập trung vào việc ôn luyện và củng cố các kiến thức cơ bản về các phép tính cộng, trừ, nhân, chia các số tự nhiên, các bài toán có liên quan đến đơn vị đo độ dài, khối lượng, thời gian. Mục tiêu chính là giúp học sinh nắm vững kiến thức nền tảng và rèn luyện kỹ năng giải toán một cách thành thạo.
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia các số tự nhiên. Để giải bài tập này, học sinh cần nắm vững các quy tắc thực hiện các phép tính và thực hiện tính toán một cách cẩn thận. Ví dụ:
Lưu ý: Khi thực hiện các phép tính, học sinh nên kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài 2 đưa ra các bài toán liên quan đến việc đổi đơn vị đo độ dài (mét, xăng-ti-mét), khối lượng (kilô-gam, gam), thời gian (giờ, phút). Để giải bài tập này, học sinh cần nắm vững các mối quan hệ giữa các đơn vị đo và thực hiện các phép đổi đơn vị một cách chính xác. Ví dụ:
Đổi 2 mét ra xăng-ti-mét: 2 mét = 2 x 100 = 200 xăng-ti-mét
Bài 3 đưa ra các bài toán ứng dụng thực tế, yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các tình huống cụ thể. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định được các thông tin quan trọng và lựa chọn phép tính phù hợp để giải quyết bài toán. Ví dụ:
Một cửa hàng có 35 kg gạo. Cửa hàng đã bán được 12 kg gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Giải: Số kg gạo còn lại là: 35 - 12 = 23 (kg)
Đáp số: 23 kg
Việc giải bài tập phát triển năng lực Toán 4 không chỉ giúp học sinh củng cố kiến thức mà còn giúp học sinh phát triển các kỹ năng quan trọng như:
Giải Phần A. Tái hiện, củng cố trang 24 Bài tập phát triển năng lực Toán 4 là một bước quan trọng trong quá trình học tập môn Toán của học sinh lớp 4. Hy vọng với hướng dẫn chi tiết và các mẹo học tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập toán và đạt kết quả tốt trong học tập.