Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho Phần B. Kết nối trang 34 Bài tập phát triển năng lực tập 2 Toán lớp 6 Kết nối tri thức.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Do đó, giaitoan.edu.vn luôn cố gắng mang đến những giải pháp tối ưu, giúp học sinh nắm vững kiến thức và tự tin hơn trong học tập.
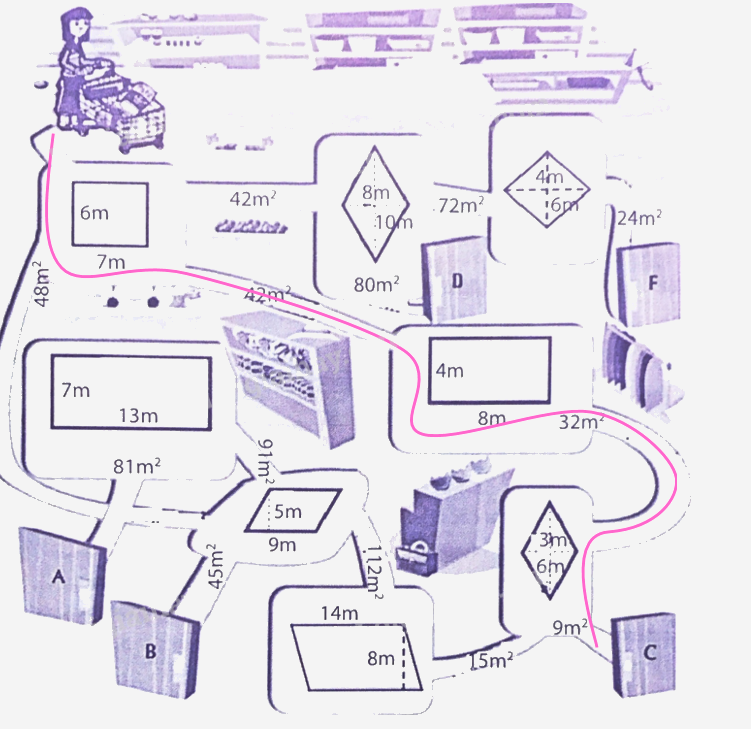
Lối ra siêu thị nằm ở vị trí của câu trả lời đúng về diện tích mỗi hình tứ giác trên đường ra. Em hãy giúp bác Mai tìm đường ra khỏi siêu thị nhé.
Một hình chữ nhật có nửa chi vi là 63 cm, chiều rộng bằng $\frac{1}{2}$ chiều dài. Tính diện tích hình chữ nhật đó.
Phương pháp giải:
- Vẽ sơ đồ
- Tìm tổng số phần bằng nhau và giá trị của 1 phần.
- Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
- Tìm số lớn (lấy tổng hai số trừ đi số bé, …).
- Tính diện tích hình chữ nhật = chiều dài x chiều rộng
Lời giải chi tiết:
Ta có sơ đồ sau:
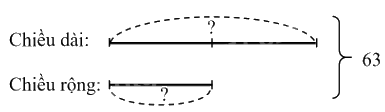
Theo sơ đồ, tổng số phần bằng nhau là:
1 + 2 = 3 (phần)
Chiều rộng hình chữ nhật là:
63 : 3 × 1 = 21 (cm)
Chiều dài hình chữ nhật là:
63 – 21 = 42 (cm)
Diện tích hình chữ nhật là:
21 x 42 = 882 (cm2)
Đáp số: 882 cm2
Khoanh vào chữ đặt trước câu trả lời đúng:
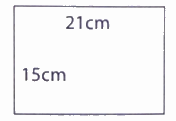
Tỉ số của chiều rộng và chiều dài của hình chữ nhật bên là:
${\text{A}}{\text{. }}\frac{{15}}{{21}}$
${\text{B}}{\text{. }}\frac{{15}}{{36}}$
${\text{C}}{\text{. }}\frac{{21}}{{36}}$
${\text{D}}{\text{. }}\frac{{21}}{{15}}$
Phương pháp giải:
Tỉ số của a và b là a : b hay $\frac{a}{b}$ (b khác 0).
Lời giải chi tiết:
Hình chữ nhật có chiều rộng là 15 cm, chiều dài là 21 cm. Vậy tỉ số của chiều rộng và chiều dài của hình chữ nhật bên là $\frac{{15}}{{21}}$.
Chọn đáp án A.
Bác Hưng là một thợ sơn lâu năm trong nghề, lần này bác sơn cho ngôi nhà của con trai mình. Tuy đã cao tuổi nhưng bác luôn tìm tòi để lựa chọn màu sơn phù hợp nhất cho ngôi nhà của con. Dưới đây là một số sơ đồ đơn giản để tạo màu sơn mới:
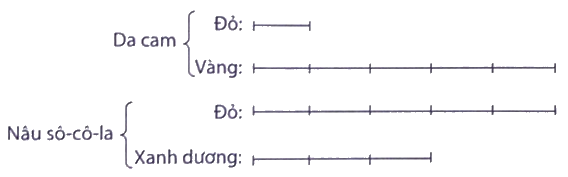
a) Em hãy nêu tỉ số giữa các màu để tạo ra hai màu sơn mới: da cam, nâu sô-cô-la.
b) Tỉ số giữa ba màu xanh dương, vàng, đỏ để tạo ra màu rêu như sau:
Tỉ số giữa màu đỏ và màu xanh dương là 1 : 5;
Tỉ số giữa màu xanh dương và màu vàng là 1 : 5.
Em hãy vẽ một sơ đồ biểu thị tỉ số giữa ba màu trên.
Phương pháp giải:
a) - Đếm số phần của mỗi màu trên sơ đồ rồi xác định tỉ số
- Tỉ số của a và b là a : b hay (b khác 0).
b) Vẽ sơ đồ theo tỉ số đã cho
Lời giải chi tiết:
a) Tỉ số giữa màu đỏ và màu vàng đêt tạo màu da cam là 1 : 5 hay $\frac{1}{5}$
Tỉ số giữa màu đỏ và màu xanh dương để tạo ra màu nâu sô-cô-la là 5 : 3 hay $\frac{5}{3}$
b)
Tỉ số giữa màu đỏ và màu xanh dương là 1 : 5; Tỉ số giữa màu xanh dương và màu vàng là 1 : 5 nên ta coi màu đỏ là 1 phần, màu xạnh dương là 5 phần, màu vàng là 25 phần bằng nhau.

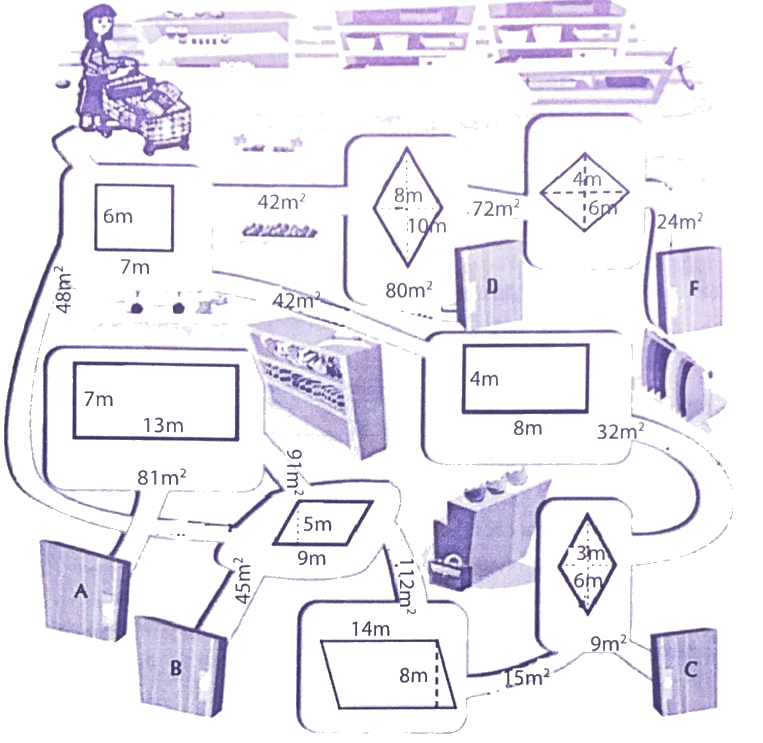
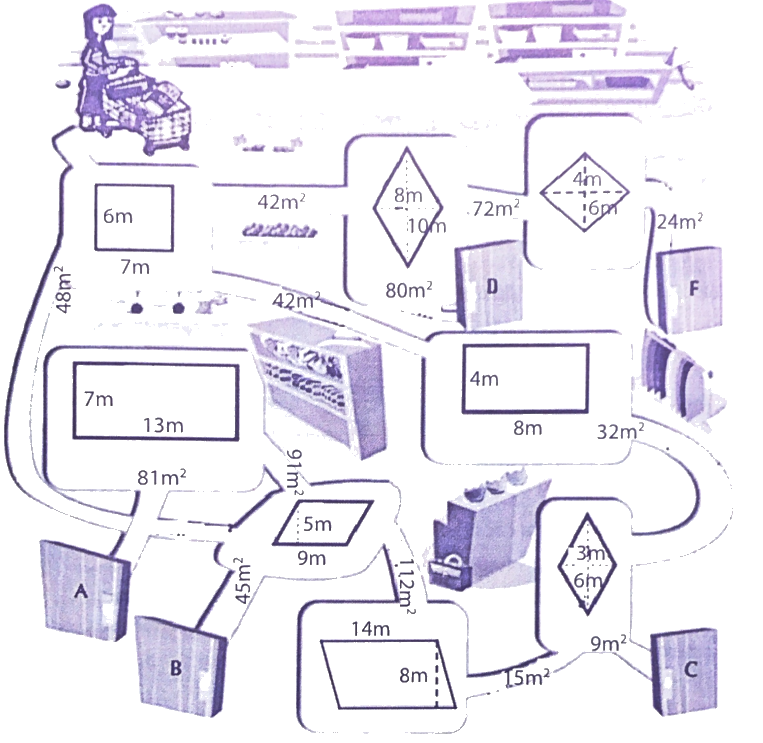
Lối ra siêu thị nằm ở vị trí của câu trả lời đúng về diện tích mỗi hình tứ giác trên đường ra. Em hãy giúp bác Mai tìm đường ra khỏi siêu thị nhé.
Phương pháp giải:
Tính diện tích mỗi hình tứ giác trên đường đi để tìm đường ra khỏi siêu thị.
Lời giải chi tiết:
Đường ra khỏi siêu thị của bác Mai như sau:
- Ngã rẽ đầu tiên, diện tích hình chữ nhật có chiều rộng 6m, chiều dài 7m là 6 x 7 = 42 m2.
- Diện tích hình chữ nhật có chiều rộng 4 m, chiều dài 8m là 4 x 8 = 32 m2.
- Diện tích hình thoi có độ dài hai đường chéo là 3m và 6m là $\frac{{3 \times 6}}{2} = 9$ m2.
Vậy cổng ra là cổng C.
Ta có hình vẽ như sau:
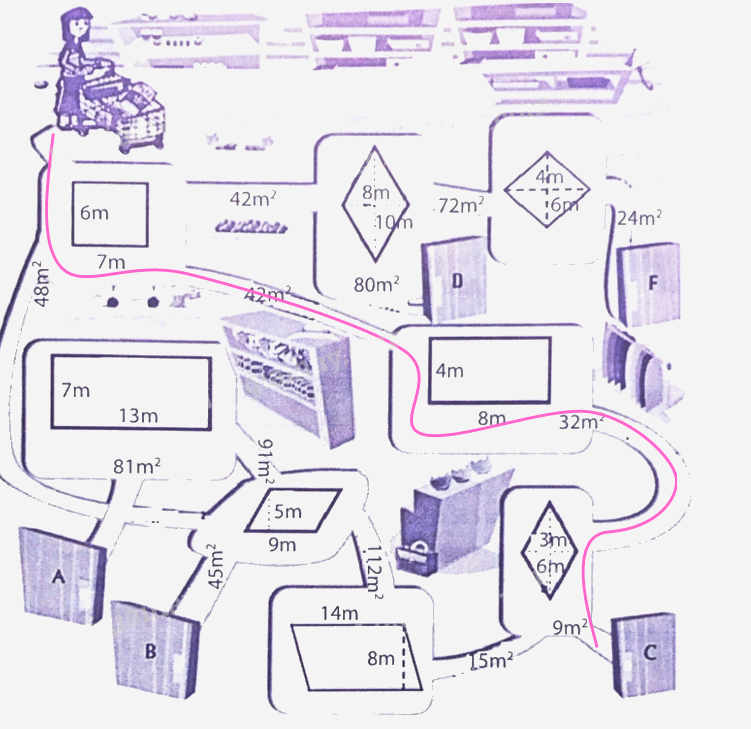
Lối ra siêu thị nằm ở vị trí của câu trả lời đúng về diện tích mỗi hình tứ giác trên đường ra. Em hãy giúp bác Mai tìm đường ra khỏi siêu thị nhé.
Phương pháp giải:
Tính diện tích mỗi hình tứ giác trên đường đi để tìm đường ra khỏi siêu thị.
Lời giải chi tiết:
Đường ra khỏi siêu thị của bác Mai như sau:
- Ngã rẽ đầu tiên, diện tích hình chữ nhật có chiều rộng 6m, chiều dài 7m là 6 x 7 = 42 m2.
- Diện tích hình chữ nhật có chiều rộng 4 m, chiều dài 8m là 4 x 8 = 32 m2.
- Diện tích hình thoi có độ dài hai đường chéo là 3m và 6m là $\frac{{3 \times 6}}{2} = 9$ m2.
Vậy cổng ra là cổng C.
Ta có hình vẽ như sau:
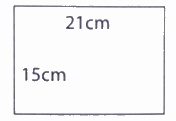
Khoanh vào chữ đặt trước câu trả lời đúng:
Tỉ số của chiều rộng và chiều dài của hình chữ nhật bên là:
${\text{A}}{\text{. }}\frac{{15}}{{21}}$
${\text{B}}{\text{. }}\frac{{15}}{{36}}$
${\text{C}}{\text{. }}\frac{{21}}{{36}}$
${\text{D}}{\text{. }}\frac{{21}}{{15}}$
Phương pháp giải:
Tỉ số của a và b là a : b hay $\frac{a}{b}$ (b khác 0).
Lời giải chi tiết:
Hình chữ nhật có chiều rộng là 15 cm, chiều dài là 21 cm. Vậy tỉ số của chiều rộng và chiều dài của hình chữ nhật bên là $\frac{{15}}{{21}}$.
Chọn đáp án A.
Một hình chữ nhật có nửa chi vi là 63 cm, chiều rộng bằng $\frac{1}{2}$ chiều dài. Tính diện tích hình chữ nhật đó.
Phương pháp giải:
- Vẽ sơ đồ
- Tìm tổng số phần bằng nhau và giá trị của 1 phần.
- Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
- Tìm số lớn (lấy tổng hai số trừ đi số bé, …).
- Tính diện tích hình chữ nhật = chiều dài x chiều rộng
Lời giải chi tiết:
Ta có sơ đồ sau:
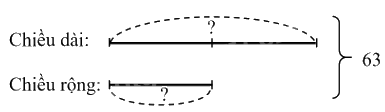
Theo sơ đồ, tổng số phần bằng nhau là:
1 + 2 = 3 (phần)
Chiều rộng hình chữ nhật là:
63 : 3 × 1 = 21 (cm)
Chiều dài hình chữ nhật là:
63 – 21 = 42 (cm)
Diện tích hình chữ nhật là:
21 x 42 = 882 (cm2)
Đáp số: 882 cm2
Bác Hưng là một thợ sơn lâu năm trong nghề, lần này bác sơn cho ngôi nhà của con trai mình. Tuy đã cao tuổi nhưng bác luôn tìm tòi để lựa chọn màu sơn phù hợp nhất cho ngôi nhà của con. Dưới đây là một số sơ đồ đơn giản để tạo màu sơn mới:
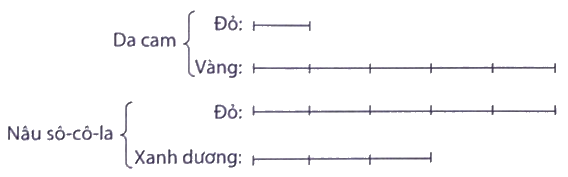
a) Em hãy nêu tỉ số giữa các màu để tạo ra hai màu sơn mới: da cam, nâu sô-cô-la.
b) Tỉ số giữa ba màu xanh dương, vàng, đỏ để tạo ra màu rêu như sau:
Tỉ số giữa màu đỏ và màu xanh dương là 1 : 5;
Tỉ số giữa màu xanh dương và màu vàng là 1 : 5.
Em hãy vẽ một sơ đồ biểu thị tỉ số giữa ba màu trên.
Phương pháp giải:
a) - Đếm số phần của mỗi màu trên sơ đồ rồi xác định tỉ số
- Tỉ số của a và b là a : b hay (b khác 0).
b) Vẽ sơ đồ theo tỉ số đã cho
Lời giải chi tiết:
a) Tỉ số giữa màu đỏ và màu vàng đêt tạo màu da cam là 1 : 5 hay $\frac{1}{5}$
Tỉ số giữa màu đỏ và màu xanh dương để tạo ra màu nâu sô-cô-la là 5 : 3 hay $\frac{5}{3}$
b)
Tỉ số giữa màu đỏ và màu xanh dương là 1 : 5; Tỉ số giữa màu xanh dương và màu vàng là 1 : 5 nên ta coi màu đỏ là 1 phần, màu xạnh dương là 5 phần, màu vàng là 25 phần bằng nhau.

Phần B. Kết nối trang 34 Bài tập phát triển năng lực tập 2 Toán lớp 6 Kết nối tri thức là một phần quan trọng trong chương trình học, giúp học sinh rèn luyện kỹ năng giải toán và áp dụng kiến thức đã học vào thực tế. Dưới đây là hướng dẫn chi tiết từng bài tập trong phần này:
Bài tập này yêu cầu học sinh hiểu rõ khái niệm tỉ số và cách tính tỉ số của hai đại lượng. Để giải bài tập này, học sinh cần xác định đúng hai đại lượng cần so sánh và áp dụng công thức tính tỉ số.
Bài tập này yêu cầu học sinh hiểu rõ khái niệm tỉ số phần trăm và cách tính tỉ số phần trăm của một số. Để giải bài tập này, học sinh cần xác định đúng số cần tính tỉ số phần trăm và chia cho 100.
Bài tập này yêu cầu học sinh hiểu rõ các đơn vị đo lường và cách chuyển đổi giữa các đơn vị đo lường khác nhau. Để giải bài tập này, học sinh cần xác định đúng đơn vị đo lường cần chuyển đổi và áp dụng công thức chuyển đổi.
Bài tập này yêu cầu học sinh hiểu rõ công thức tính diện tích hình chữ nhật và cách áp dụng công thức này để giải bài tập. Để giải bài tập này, học sinh cần xác định đúng chiều dài và chiều rộng của hình chữ nhật và áp dụng công thức diện tích = chiều dài * chiều rộng.
| Chiều dài | Chiều rộng | Diện tích |
|---|---|---|
| 5 cm | 3 cm | 15 cm² |
| 8 m | 4 m | 32 m² |
Bài tập này yêu cầu học sinh hiểu rõ công thức tính chu vi hình chữ nhật và cách áp dụng công thức này để giải bài tập. Để giải bài tập này, học sinh cần xác định đúng chiều dài và chiều rộng của hình chữ nhật và áp dụng công thức chu vi = 2 * (chiều dài + chiều rộng).
Lưu ý: Khi giải các bài toán về tỉ số, tỉ số phần trăm, đơn vị đo lường, diện tích và chu vi hình chữ nhật, học sinh cần đọc kỹ đề bài, xác định đúng các yếu tố cần thiết và áp dụng công thức phù hợp. Ngoài ra, học sinh cũng nên kiểm tra lại kết quả để đảm bảo tính chính xác.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải Phần B. Kết nối trang 34 Bài tập phát triển năng lực tập 2 Toán lớp 6 Kết nối tri thức. Chúc các em học tốt!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức toán học.