Bài tập phát triển năng lực Toán 4 tập 2 trang 18 phần B là một phần quan trọng giúp học sinh rèn luyện và củng cố kiến thức đã học. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh tự tin giải bài tập.
Chúng tôi không chỉ cung cấp đáp án mà còn giải thích rõ ràng từng bước, giúp các em hiểu bản chất của bài toán và áp dụng vào các bài tập tương tự.
Một hình bình hành có một cạnh dài 2/5 m, một cạnh dài 1/4 m ....Rút gọn rồi tính ....
Một hình bình hành có một cạnh dài \(\frac{2}{5}m\), một cạnh dài \(\frac{1}{4}m\). Tính nửa chu vi của hình bình hành đó.
Phương pháp giải:
Nửa chu vi hình bình hành bằng tổng độ dài hai cạnh liên tiếp của hình bình hành đó.
Lời giải chi tiết:
Nửa chu vi hình bình hành là:
\(\frac{2}{5} + \frac{1}{4} = \frac{{13}}{{20}}(m)\)
Đáp số: \(\frac{{13}}{{20}}m\)
Rút gọn rồi tính:
\(\frac{{15}}{{35}} - \frac{2}{{14}} = ....................\)
\(\frac{{33}}{{18}} - \frac{5}{{30}} = ....................{\text{ }}\)
\(\frac{6}{{45}} - \frac{2}{{30}} = ..........................\)
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
\(\frac{{15}}{{35}} - \frac{2}{{14}} = \frac{3}{7} - \frac{1}{7}{\text{ = }}\frac{2}{7}\)
\(\frac{{33}}{{18}} - \frac{5}{{30}} = \frac{{11}}{6} - \frac{1}{6}{\text{ = }}\frac{{10}}{6}{\text{ = }}\frac{5}{3}\)
\(\frac{6}{{45}} - \frac{2}{{30}} = \frac{2}{{15}} - \frac{1}{{15}} = \frac{1}{{15}}\)
Mẹ Thuý là thợ may. Hôm nay mẹ nhận may áo cho một số bé gái. Mẹ lấy một tấm vải và cắt $\frac{8}{{15}}$ tấm vải để may. Hỏi sau khi cắt, còn lại bao nhiêu phần của tấm vải?
Phương pháp giải:
- Coi cả tấm vải là 1 đơn vị.
- Muốn tìm số phần còn lại của tấm vải ta lấy 1 trừ đi số phần tấm vải đã cắt.
Lời giải chi tiết:
Số phần còn lại của tấm vải sau khi cắt là:
\(1 - \frac{8}{{15}} = \frac{7}{{15}}\) (tấm vải)
Đáp số: $\frac{7}{{15}}$ tấm vải.
Đúng ghi Đ, sai ghi S:
\({\text{a) }}\frac{{13}}{{15}} - \frac{8}{{15}} = \frac{{13 - 8}}{{15}} = \frac{2}{5}{\text{ }}\)
\({\text{b) }}\frac{{17}}{{32}} - \frac{{13}}{{32}} = \frac{{17 - 13}}{{32}} = \frac{4}{{32}}{\text{ }}\)
\({\text{c) }}\frac{8}{{16}} - \frac{3}{8} = \frac{4}{8} - \frac{3}{8} = \frac{{4 - 3}}{8} = \frac{1}{8}{\text{ }}\)
\({\text{d) }}\frac{{17}}{{19}} - \frac{1}{9} = \frac{{17 - 1}}{{19}} = \frac{{16}}{{19}}{\text{ }}\)
Phương pháp giải:
Kiểm tra lại cách cộng trừ phân số rồi xét tính đúng sai của từng câu.
Áp dụng kiến thức:
- Muốn trừ hai phân số khác mẫu số ta trừ tử số cho nhau và giữ nguyên mẫu số.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số rồi trừ hai phân số đó.
Lời giải chi tiết:

Tìm x, biết:
\(x + \frac{5}{6} = \frac{7}{6}\)
\(\frac{{48}}{{54}} - x = \frac{7}{8}\)
\(\frac{5}{{12}} + x = \frac{9}{{12}}\)
\(\frac{{55}}{{60}} - x = \frac{{30}}{{45}}\)
Phương pháp giải:
- Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
- Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
- Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
Lời giải chi tiết:
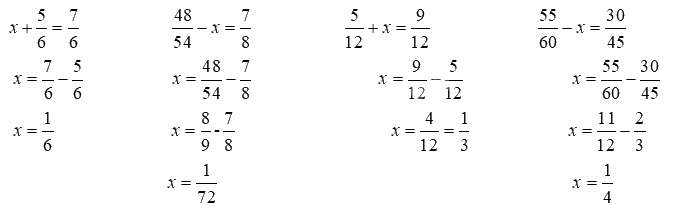
Rút gọn rồi tính:
\(3 - \frac{{17}}{{51}} = ...............\)
\(\frac{{72}}{{27}} - 1 = .............\)
\(6 - \frac{{240}}{{160}} = ..............\)
\(\frac{{1800}}{{400}} - 3 = ..............\)
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản.
- Ta có thể viết các số tự nhiên dưới dạng phân số có mẫu số là 1, sau đó thực hiện phép trừ hai phân số như thông thường.
Lời giải chi tiết:
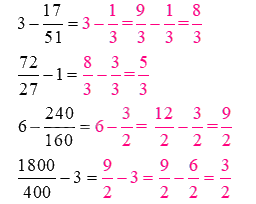
Tính giá trị của biểu thức:
\({\text{a) }}\frac{2}{{13}} + \frac{4}{7} - \frac{1}{3}\)
\({\text{b) }}\frac{{13}}{{120}} + \frac{{11}}{{24}} - \frac{{17}}{{30}}\)
\({\text{c) }}\frac{{18}}{{100}} + \frac{9}{{45}} - \frac{2}{{25}}\)
Phương pháp giải:
Thực hiện tính theo thứ tự từ trái sang phải.
Lời giải chi tiết:
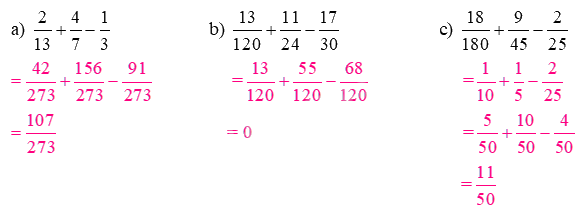
Một hình bình hành có một cạnh dài \(\frac{2}{5}m\), một cạnh dài \(\frac{1}{4}m\). Tính nửa chu vi của hình bình hành đó.
Phương pháp giải:
Nửa chu vi hình bình hành bằng tổng độ dài hai cạnh liên tiếp của hình bình hành đó.
Lời giải chi tiết:
Nửa chu vi hình bình hành là:
\(\frac{2}{5} + \frac{1}{4} = \frac{{13}}{{20}}(m)\)
Đáp số: \(\frac{{13}}{{20}}m\)
Tìm x, biết:
\(x + \frac{5}{6} = \frac{7}{6}\)
\(\frac{{48}}{{54}} - x = \frac{7}{8}\)
\(\frac{5}{{12}} + x = \frac{9}{{12}}\)
\(\frac{{55}}{{60}} - x = \frac{{30}}{{45}}\)
Phương pháp giải:
- Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
- Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
- Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
Lời giải chi tiết:
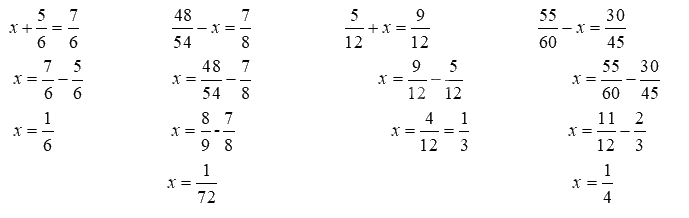
Đúng ghi Đ, sai ghi S:
\({\text{a) }}\frac{{13}}{{15}} - \frac{8}{{15}} = \frac{{13 - 8}}{{15}} = \frac{2}{5}{\text{ }}\)
\({\text{b) }}\frac{{17}}{{32}} - \frac{{13}}{{32}} = \frac{{17 - 13}}{{32}} = \frac{4}{{32}}{\text{ }}\)
\({\text{c) }}\frac{8}{{16}} - \frac{3}{8} = \frac{4}{8} - \frac{3}{8} = \frac{{4 - 3}}{8} = \frac{1}{8}{\text{ }}\)
\({\text{d) }}\frac{{17}}{{19}} - \frac{1}{9} = \frac{{17 - 1}}{{19}} = \frac{{16}}{{19}}{\text{ }}\)
Phương pháp giải:
Kiểm tra lại cách cộng trừ phân số rồi xét tính đúng sai của từng câu.
Áp dụng kiến thức:
- Muốn trừ hai phân số khác mẫu số ta trừ tử số cho nhau và giữ nguyên mẫu số.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số rồi trừ hai phân số đó.
Lời giải chi tiết:

Rút gọn rồi tính:
\(\frac{{15}}{{35}} - \frac{2}{{14}} = ....................\)
\(\frac{{33}}{{18}} - \frac{5}{{30}} = ....................{\text{ }}\)
\(\frac{6}{{45}} - \frac{2}{{30}} = ..........................\)
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
\(\frac{{15}}{{35}} - \frac{2}{{14}} = \frac{3}{7} - \frac{1}{7}{\text{ = }}\frac{2}{7}\)
\(\frac{{33}}{{18}} - \frac{5}{{30}} = \frac{{11}}{6} - \frac{1}{6}{\text{ = }}\frac{{10}}{6}{\text{ = }}\frac{5}{3}\)
\(\frac{6}{{45}} - \frac{2}{{30}} = \frac{2}{{15}} - \frac{1}{{15}} = \frac{1}{{15}}\)
Rút gọn rồi tính:
\(3 - \frac{{17}}{{51}} = ...............\)
\(\frac{{72}}{{27}} - 1 = .............\)
\(6 - \frac{{240}}{{160}} = ..............\)
\(\frac{{1800}}{{400}} - 3 = ..............\)
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản.
- Ta có thể viết các số tự nhiên dưới dạng phân số có mẫu số là 1, sau đó thực hiện phép trừ hai phân số như thông thường.
Lời giải chi tiết:
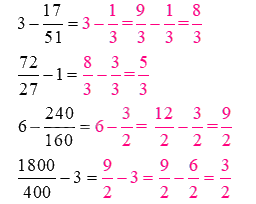
Mẹ Thuý là thợ may. Hôm nay mẹ nhận may áo cho một số bé gái. Mẹ lấy một tấm vải và cắt $\frac{8}{{15}}$ tấm vải để may. Hỏi sau khi cắt, còn lại bao nhiêu phần của tấm vải?
Phương pháp giải:
- Coi cả tấm vải là 1 đơn vị.
- Muốn tìm số phần còn lại của tấm vải ta lấy 1 trừ đi số phần tấm vải đã cắt.
Lời giải chi tiết:
Số phần còn lại của tấm vải sau khi cắt là:
\(1 - \frac{8}{{15}} = \frac{7}{{15}}\) (tấm vải)
Đáp số: $\frac{7}{{15}}$ tấm vải.
Tính giá trị của biểu thức:
\({\text{a) }}\frac{2}{{13}} + \frac{4}{7} - \frac{1}{3}\)
\({\text{b) }}\frac{{13}}{{120}} + \frac{{11}}{{24}} - \frac{{17}}{{30}}\)
\({\text{c) }}\frac{{18}}{{100}} + \frac{9}{{45}} - \frac{2}{{25}}\)
Phương pháp giải:
Thực hiện tính theo thứ tự từ trái sang phải.
Lời giải chi tiết:
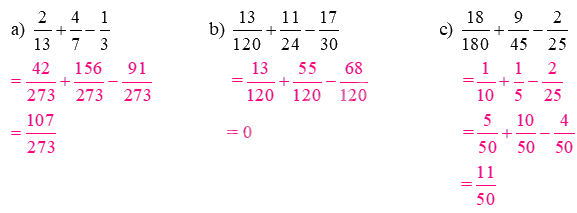
Bài tập phần B trang 18 Toán 4 tập 2 thuộc chương trình Kết nối tri thức, tập trung vào việc vận dụng các kiến thức đã học về các phép tính với số có nhiều chữ số, đặc biệt là phép cộng, trừ, nhân, chia và các bài toán có liên quan đến đơn vị đo độ dài, khối lượng, thời gian.
Bài 1 yêu cầu học sinh thực hiện các phép cộng và trừ với các số có nhiều chữ số. Để giải bài này, học sinh cần nắm vững quy tắc cộng và trừ các số tự nhiên, đặc biệt là việc thực hiện các phép cộng và trừ có nhớ, có mượn.
Bài 2 yêu cầu học sinh thực hiện các phép nhân và chia với các số có nhiều chữ số. Để giải bài này, học sinh cần nắm vững bảng nhân, bảng chia và quy tắc nhân, chia các số tự nhiên.
Bài 3 yêu cầu học sinh vận dụng kiến thức về các đơn vị đo độ dài, khối lượng, thời gian để giải bài toán. Để giải bài này, học sinh cần nắm vững mối quan hệ giữa các đơn vị đo khác nhau và biết cách chuyển đổi giữa chúng.
Ví dụ, để chuyển đổi từ mét sang centimet, ta nhân số mét với 100. Để chuyển đổi từ kilogram sang gram, ta nhân số kilogram với 1000.
Bài 4 là một bài toán tổng hợp, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết một tình huống thực tế. Để giải bài này, học sinh cần đọc kỹ đề bài, xác định các thông tin quan trọng và lựa chọn phương pháp giải phù hợp.
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp các bài giảng, bài tập và lời giải chi tiết cho học sinh Toán 4. Chúng tôi cam kết mang đến cho học sinh một môi trường học tập hiệu quả, giúp các em tự tin chinh phục môn Toán.
Các lợi ích khi học Toán 4 tại giaitoan.edu.vn:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để bắt đầu hành trình chinh phục môn Toán!