Chào mừng các em học sinh đến với lời giải chi tiết Bài 1 trang 83 Sách Bài Tập Toán 7 Tập 1 - Chân Trời Sáng Tạo. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em ôn tập và nắm vững kiến thức toán học.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải bài tập một cách dễ hiểu, giúp các em tự tin hơn trong quá trình học tập và làm bài.
Cho biết a // b, tìm các số đo x trong Hình 10.
Đề bài
Cho biết a // b, tìm các số đo x trong Hình 10.
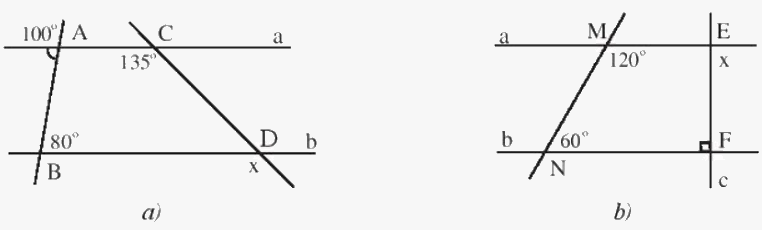
Phương pháp giải - Xem chi tiết
Ta sử dụng tính chất: Nếu 2 đường thẳng cắt 2 đường thẳng song song thì tạo thành cặp góc so le trong bằng nhau; cặp góc đồng vị bằng nhau.
Lời giải chi tiết
a) Vì \(a // b \Rightarrow x=\widehat {ACD}\) (hai góc đồng vị).
Mà \(\widehat {ACD}=135^0\)
\(\Rightarrow x= 135^0\)
b) Vì \(a // b \Rightarrow x=\widehat {NFE}\) (hai góc so le trong).
Mà \(\widehat {NFE}=90^0\)
\(\Rightarrow x= 90^0\)
Bài 1 trang 83 Sách Bài Tập Toán 7 Tập 1 - Chân Trời Sáng Tạo thuộc chương trình học toán 7, tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các quy tắc, tính chất của các phép toán và biết cách áp dụng chúng một cách linh hoạt.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giải quyết hiệu quả Bài 1 trang 83, học sinh cần nắm vững các phương pháp sau:
Bài tập: Tính giá trị của biểu thức sau: (1/2) + (2/3) - (1/4)
Giải:
Để tính giá trị của biểu thức, ta cần quy đồng mẫu số của các phân số:
(1/2) + (2/3) - (1/4) = (6/12) + (8/12) - (3/12) = (6 + 8 - 3)/12 = 11/12
Vậy, giá trị của biểu thức là 11/12.
Dưới đây là một số lưu ý quan trọng khi giải Bài 1 trang 83:
Ngoài sách bài tập, học sinh có thể tham khảo thêm các tài liệu sau để học toán 7 hiệu quả hơn:
Bài 1 trang 83 Sách Bài Tập Toán 7 Tập 1 - Chân Trời Sáng Tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về số hữu tỉ và các phép toán. Bằng cách nắm vững các phương pháp giải và thực hành thường xuyên, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt trong môn toán.