Giaitoan.edu.vn xin giới thiệu lời giải chi tiết Bài 4 trang 86 sách bài tập Toán 7 Tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải chi tiết, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chứng minh định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.
Đề bài
Chứng minh định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.
Phương pháp giải - Xem chi tiết
Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.
Lời giải chi tiết
Hình vẽ minh họa:
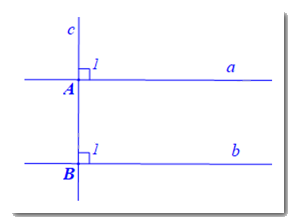
Viết giả thiết và kết luận bằng kí hiệu:
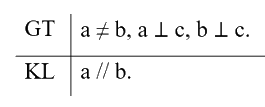
Chứng minh định lí:
Vì a ⊥ c (GT) nên \(\widehat {{A_1}}\)=90°
Vì b ⊥ c (GT) nên \(\widehat {{B_1}}\)=90°
Do đó \(\widehat {{A_1}}\) = \(\widehat {{B_1}}\) (=90°)
Mà \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\) ở vị trí đồng vị
Suy ra a // b (Dấu hiệu nhận biết 2 đường thẳng song song).
Vậy a // b.
Bài 4 trang 86 sách bài tập Toán 7 Tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán trên số hữu tỉ để giải quyết các bài toán thực tế.
Bài 4 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia các số hữu tỉ. Các số hữu tỉ có thể được biểu diễn dưới dạng phân số, số thập phân hoặc phần trăm. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép toán trên số hữu tỉ, bao gồm:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày chi tiết lời giải cho từng câu hỏi:
Câu a yêu cầu tính giá trị của biểu thức: (1/2) + (1/3). Để giải câu này, ta cần quy đồng mẫu số của hai phân số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Do đó, ta có:
(1/2) + (1/3) = (3/6) + (2/6) = (3+2)/6 = 5/6
Câu b yêu cầu tính giá trị của biểu thức: (2/5) - (1/4). Tương tự như câu a, ta cần quy đồng mẫu số của hai phân số. Mẫu số chung nhỏ nhất của 5 và 4 là 20. Do đó, ta có:
(2/5) - (1/4) = (8/20) - (5/20) = (8-5)/20 = 3/20
Câu c yêu cầu tính giá trị của biểu thức: (3/4) * (2/7). Để giải câu này, ta nhân tử số với tử số và mẫu số với mẫu số:
(3/4) * (2/7) = (3*2)/(4*7) = 6/28 = 3/14
Câu d yêu cầu tính giá trị của biểu thức: (5/6) : (1/2). Để giải câu này, ta nhân số bị chia với nghịch đảo của số chia:
(5/6) : (1/2) = (5/6) * (2/1) = (5*2)/(6*1) = 10/6 = 5/3
Khi giải bài tập về các phép toán trên số hữu tỉ, học sinh cần lưu ý những điều sau:
Bài tập về các phép toán trên số hữu tỉ có ứng dụng rất lớn trong thực tế. Ví dụ, trong lĩnh vực tài chính, các phép toán này được sử dụng để tính lãi suất, tỷ giá hối đoái, và các khoản chi phí khác. Trong lĩnh vực khoa học, các phép toán này được sử dụng để tính toán các đại lượng vật lý, hóa học, và sinh học.
Để rèn luyện kỹ năng giải bài tập về các phép toán trên số hữu tỉ, học sinh có thể làm thêm các bài tập tương tự sau:
Hy vọng rằng, với hướng dẫn chi tiết này, học sinh sẽ hiểu rõ hơn về cách giải Bài 4 trang 86 sách bài tập Toán 7 Tập 1 - Chân trời sáng tạo và tự tin làm bài tập.