Chào mừng các em học sinh đến với lời giải chi tiết Bài 4 trang 33 sách bài tập Toán 7 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Hãy lập biểu thức có dạng đa thức theo biến \(x\) biểu thị diện tích của phần được tô đậm trong Hình 1.
Đề bài
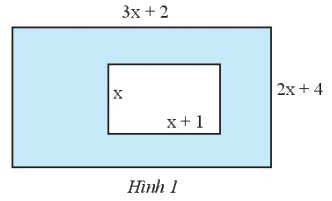
Hãy lập biểu thức có dạng đa thức theo biến \(x\) biểu thị diện tích của phần được tô đậm trong Hình 1.
Phương pháp giải - Xem chi tiết
Sử dụng các công thức tính diện tích đã học để viết được biểu thức.
Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng
Lời giải chi tiết
Diện tích hình chữ nhật lớn là \(\left( {3x + 2} \right)\left( {2x + 4} \right) = 2x.3x + 2x.2 + 4.3x + 4.2 = 6{x^2} + 16x + 8\).
Diện tích hình chữ nhật nhỏ là \(x\left( {x + 1} \right) = {x^2} + x\).
Diện tích cần tìm là \(6{x^2} + 16x + 8 - \left( {{x^2} + x} \right) = 5{x^2} + 15x + 8\).
Bài 4 trang 33 sách bài tập Toán 7 Chân trời sáng tạo thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các quy tắc, tính chất của các phép toán và biết cách áp dụng chúng một cách linh hoạt.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 4 trang 33 một cách hiệu quả, học sinh cần:
Ví dụ: Tính giá trị của biểu thức sau: (1/2) + (2/3) - (1/6)
Giải:
Để tính giá trị của biểu thức, ta thực hiện các bước sau:
Vậy, giá trị của biểu thức là 1.
Khi giải bài 4 trang 33, học sinh cần lưu ý những điều sau:
Để hỗ trợ học sinh trong quá trình giải bài tập, giaitoan.edu.vn cung cấp các tài liệu tham khảo sau:
Bài 4 trang 33 sách bài tập Toán 7 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về số hữu tỉ và các phép toán. Bằng cách nắm vững các kiến thức cơ bản, áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, các em sẽ có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!