Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho Bài 3 trang 83 sách bài tập Toán 7 tập 1, chương trình Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự giải bài tập đôi khi gặp khó khăn, đặc biệt là với những em mới làm quen với chương trình.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập, cung cấp các giải pháp học toán hiệu quả và chất lượng. Hãy cùng khám phá lời giải chi tiết ngay sau đây!
a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua đỉnh A và song song với BC, cách vẽ đường thẳng b đi qua B và song song với AC. b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?
Đề bài
a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua đỉnh A và song song với BC, cách vẽ đường thẳng b đi qua B và song song với AC.
b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?
Phương pháp giải - Xem chi tiết
Ta sử dụng tiên đề Eculid và các tính chất 2 góc so le trong, đồng vị để vẽ hình.
Lời giải chi tiết
a) Ta vẽ đường thẳng xy đi qua A sao cho \(\widehat {xAB}\)=\(\widehat {ABC}\)
Vì \(\widehat {xAB}\)=\(\widehat {ABC}\) mà hai góc này ở vị trí so le trong
Nên xy // BC.
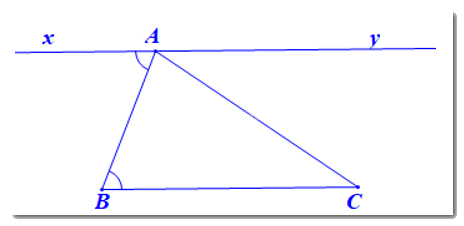
Vậy đường thẳng xy là đường thẳng cần vẽ đi qua A và song song với BC.
Ta vẽ đường thẳng zt đi qua B sao cho \(\widehat {tBC}\)=\(\widehat {BCA}\)
Vì \(\widehat {tBC}\)=\(\widehat {BCA}\) mà hai góc này ở vị trí so le trong
Nên zt // AC.
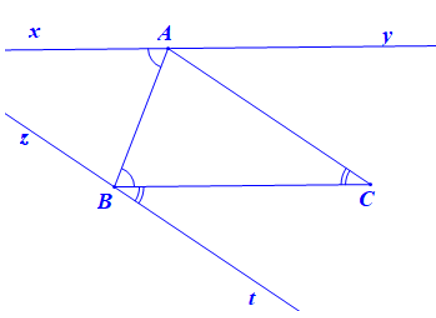
Vậy đường thẳng zt là đường thẳng cần vẽ đi qua B và song song với AC.
b) Theo tiên đề Euclid ta có qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Vậy ta chỉ vẽ được một đường thẳng a và một đường thẳng b.
Bài 3 trong sách bài tập Toán 7 tập 1 chương trình Chân trời sáng tạo tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Bài tập yêu cầu học sinh phải hiểu rõ các quy tắc, tính chất của các phép toán này và biết cách áp dụng chúng một cách linh hoạt.
Bài 3 bao gồm các dạng bài tập sau:
Để tính phần a, ta cần thực hiện các phép tính theo thứ tự ưu tiên. Ví dụ, nếu biểu thức là (1/2) + (2/3) * (4/5), ta cần thực hiện phép nhân trước, sau đó mới thực hiện phép cộng.
Ví dụ: (1/2) + (2/3) * (4/5) = (1/2) + (8/15) = (15/30) + (16/30) = 31/30
Tương tự như phần a, ta cần thực hiện các phép tính theo thứ tự ưu tiên. Lưu ý đến việc quy đồng mẫu số khi cộng hoặc trừ các phân số.
Ví dụ: (3/4) - (1/2) * (2/5) = (3/4) - (1/5) = (15/20) - (4/20) = 11/20
Đối với các biểu thức phức tạp hơn, ta có thể sử dụng các quy tắc biến đổi biểu thức để đơn giản hóa trước khi tính toán.
Ví dụ: (1/3) * (5/7) + (2/7) * (1/3) = (1/3) * (5/7 + 2/7) = (1/3) * (7/7) = (1/3) * 1 = 1/3
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Bài 3 trang 83 sách bài tập Toán 7 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính toán và giải quyết các bài toán liên quan đến số hữu tỉ. Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên, các em học sinh sẽ tự tin hơn khi làm bài tập.
| Phép toán | Công thức |
|---|---|
| Cộng | a/b + c/d = (ad + bc) / bd |
| Trừ | a/b - c/d = (ad - bc) / bd |
| Nhân | a/b * c/d = (ac) / (bd) |
| Chia | a/b : c/d = a/b * d/c = (ad) / (bc) |