Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho Bài 2 trang 45 sách bài tập Toán 7 tập một, chương trình Chân trời sáng tạo. Chúng tôi sẽ giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập, từ đó nâng cao kết quả học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập, cung cấp tài liệu và giải pháp học tập hiệu quả.
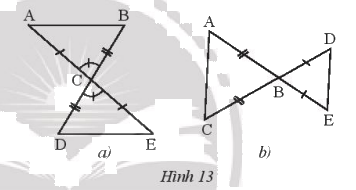
Hai tam giác trong hình 13a, 13b có bằng nhau không? Vì sao?
Đề bài
Hai tam giác trong hình 13a, 13b có bằng nhau không? Vì sao?
Phương pháp giải - Xem chi tiết
Kiểm tra các trường hợp bằng nhau của hai tam giác bằng nhau.
Lời giải chi tiết
* Hình 13a: Xét \(\Delta ACB\) và \(\Delta ECD\) có:
AC = EC (gt)
\(\widehat {ACB} = \widehat {ECD} \) (2 góc đối đỉnh)
BC = DC (gt)
Suy ra: \(\Delta ACB = \Delta ECD (c - g - c)\)
* Hình 14a: Hai tam giác ABC và DBC không bằng nhau vì hai tam giác ABC và DBC không có cặp cạnh tương ứng nào bằng nhau.
Bài 2 trang 45 sách bài tập Toán 7 Chân trời sáng tạo thuộc chương trình học Toán 7 tập một, tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các quy tắc, tính chất của các phép toán và khả năng áp dụng linh hoạt vào các tình huống khác nhau.
Bài 2 thường bao gồm các dạng bài tập sau:
Để giải Bài 2 trang 45 sách bài tập Toán 7 Chân trời sáng tạo một cách hiệu quả, bạn cần:
Bài toán: Tính giá trị của biểu thức sau: (1/2) + (2/3) - (3/4)
Giải:
Để tính giá trị của biểu thức, ta cần tìm mẫu số chung của các phân số. Mẫu số chung nhỏ nhất của 2, 3 và 4 là 12.
Ta quy đồng các phân số:
Thay các phân số đã quy đồng vào biểu thức, ta có:
(6/12) + (8/12) - (9/12) = (6 + 8 - 9)/12 = 5/12
Vậy, giá trị của biểu thức là 5/12.
Khi giải các bài tập về số hữu tỉ, bạn cần lưu ý:
Để học tốt môn Toán 7, bạn có thể tham khảo thêm các tài liệu sau:
Bài 2 trang 45 sách bài tập Toán 7 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về số hữu tỉ và các phép toán trên số hữu tỉ. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!