Giaitoan.edu.vn xin giới thiệu lời giải chi tiết Bài 3 trang 57 sách bài tập Toán 7 tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải cụ thể, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Một cái bể có kích thước như Hình 6. Bề dày bể cả bốn phía và đáy là
Đề bài
Một cái bể có kích thước như Hình 6. Bề dày bể cả bốn phía và đáy là \(\dfrac{1}{4}\) inch.
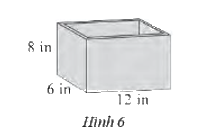
Tính thể tích của bể.
Phương pháp giải - Xem chi tiết
Ta cần tính thể tích thực bên trong của bể, khi đó ta cần tính chiều dài, rộng, cao trong lòng bể.
Lời giải chi tiết
Chiều rộng của lòng bể (không kể phần thành bể) là: \(6 - \dfrac{1}{4} - \dfrac{1}{4} = \dfrac{{11}}{2}\)(in).
Chiều dài của lòng bể (không kể phần thành bể) là: \(12 - \dfrac{1}{4} - \dfrac{1}{4} = \dfrac{{23}}{2}\) (in).
Chiều cao của lòng bể (không kể phần thành bể) là: \(8 - \dfrac{1}{4} = \dfrac{{31}}{4}\) (in). (do bể không có nắp nên chiều cao lòng bể = chiều cao bể - bề dày của phần đáy bể).
Thể tích của bể là: V = \(\dfrac{{11}}{2}.\dfrac{{23}}{2}.\dfrac{{31}}{4} = \dfrac{{7843}}{{16}} = 490,1875\) (in3).
Bài 3 trang 57 sách bài tập Toán 7 tập 1 - Chân trời sáng tạo thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về số nguyên, số hữu tỉ, các phép toán trên số nguyên và số hữu tỉ để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm, định nghĩa và các quy tắc toán học cơ bản.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải bài tập này, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán (nhân, chia trước; cộng, trừ sau) và các quy tắc về dấu của số nguyên và số hữu tỉ. Ví dụ:
Tính: (-3) + 5 - (-2) + 1
Giải:
Vậy, (-3) + 5 - (-2) + 1 = 5
Để so sánh các số, học sinh cần chuyển chúng về cùng dạng (ví dụ: cùng là số nguyên, cùng là số hữu tỉ). Sau đó, áp dụng các quy tắc so sánh số nguyên và số hữu tỉ.
Ví dụ: So sánh -2/3 và 1/2
Giải:
Ta có: -2/3 = -4/6 và 1/2 = 3/6
Vì -4 < 3 nên -4/6 < 3/6, hay -2/3 < 1/2
Để tìm x, học sinh cần thực hiện các phép toán ngược lại với các phép toán trong phương trình. Ví dụ:
Tìm x biết: x + 3 = 7
Giải:
x = 7 - 3
x = 4
Để giải bài toán thực tế, học sinh cần đọc kỹ đề bài, xác định các dữ kiện và yêu cầu của bài toán. Sau đó, vận dụng các kiến thức đã học để giải quyết bài toán.
Ví dụ: Một cửa hàng bán được 25 kg gạo trong ngày đầu tiên và 30 kg gạo trong ngày thứ hai. Hỏi trung bình mỗi ngày cửa hàng bán được bao nhiêu kg gạo?
Giải:
Tổng số gạo bán được trong hai ngày là: 25 + 30 = 55 kg
Trung bình mỗi ngày cửa hàng bán được: 55 / 2 = 27.5 kg
Ngoài sách bài tập, học sinh có thể tham khảo thêm các tài liệu sau:
Bài 3 trang 57 sách bài tập Toán 7 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.