Giải Bài 2 trang 87 sách bài tập toán 7 tập 1 - Chân trời sáng tạo

Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho Bài 2 trang 87 sách bài tập Toán 7 tập 1, chương trình Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự giải bài tập đôi khi gặp khó khăn, đặc biệt là với những em mới làm quen với chương trình.

Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trong quá trình học tập, cung cấp các giải pháp học toán hiệu quả và chất lượng. Hãy cùng khám phá lời giải chi tiết ngay sau đây!

Hãy kể tên các cặp góc đối đỉnh trong Hình 2.

Đề bài

Hãy kể tên các cặp góc đối đỉnh trong Hình 2.

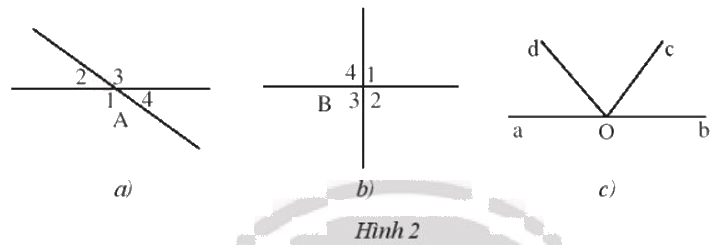
Giải Bài 2 trang 87 sách bài tập toán 7 tập 1 - Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiết Giải Bài 2 trang 87 sách bài tập toán 7 tập 1 - Chân trời sáng tạo 2

Ta sử dụng định nghĩa về 2 góc đổi đỉnh (chú ý tới các tia tạo nên góc đó)

Lời giải chi tiết

a) Các cặp góc đối đỉnh trong hình là: \(\widehat {{A_1}}\) và \(\widehat {{A_3}}\); \(\widehat {{A_2}}\) và \(\widehat {{A_4}}\).

b) Các cặp góc đối đỉnh trong hình là: \(\widehat {{B_1}}\) và \(\widehat {{B_3}}\); \(\widehat {{B_2}}\) và \(\widehat {{B_4}}\).

c) Trong hình không có cặp góc nào đối đỉnh do chỉ có tia Oa là tia đối của tia Ob nhưng tia Oc không là tia đối của tia Od.

Khai phá tiềm năng Toán lớp 7 của bạn! Đừng bỏ lỡ Giải Bài 2 trang 87 sách bài tập toán 7 tập 1 - Chân trời sáng tạo tại chuyên mục giải bài tập toán 7 trên toán học. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, cập nhật chính xác theo chương trình sách giáo khoa, các em sẽ tự tin ôn luyện, củng cố kiến thức vững chắc và nâng cao khả năng tư duy. Phương pháp học trực quan, sinh động sẽ mang lại hiệu quả học tập vượt trội mà bạn hằng mong muốn!

Giải Bài 2 trang 87 sách bài tập Toán 7 tập 1 - Chân trời sáng tạo: Tổng quan

Bài 2 trang 87 sách bài tập Toán 7 tập 1 chương trình Chân trời sáng tạo thuộc chủ đề về các phép toán với số hữu tỉ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để thực hiện các phép cộng, trừ, nhân, chia số hữu tỉ, đồng thời rèn luyện kỹ năng tính toán và tư duy logic.

Nội dung chi tiết Bài 2

Bài 2 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh thực hiện các phép tính cụ thể. Để giải bài tập này một cách chính xác, học sinh cần nắm vững các quy tắc sau:

Phép cộng và trừ số hữu tỉ: Để cộng hoặc trừ hai số hữu tỉ, ta cần quy đồng mẫu số của chúng. Sau đó, ta cộng hoặc trừ các tử số và giữ nguyên mẫu số chung.
Phép nhân số hữu tỉ: Để nhân hai số hữu tỉ, ta nhân các tử số với nhau và nhân các mẫu số với nhau.
Phép chia số hữu tỉ: Để chia hai số hữu tỉ, ta nhân số bị chia với nghịch đảo của số chia.

Lời giải chi tiết

Dưới đây là lời giải chi tiết cho từng câu hỏi trong Bài 2 trang 87 sách bài tập Toán 7 tập 1 - Chân trời sáng tạo:

Câu a)

Đề bài: Tính 1/2 + 1/3

Lời giải:

Quy đồng mẫu số: 1/2 = 3/6 và 1/3 = 2/6
Cộng hai phân số: 3/6 + 2/6 = 5/6
Vậy, 1/2 + 1/3 = 5/6

Câu b)

Đề bài: Tính 2/5 - 1/4

Lời giải:

Quy đồng mẫu số: 2/5 = 8/20 và 1/4 = 5/20
Trừ hai phân số: 8/20 - 5/20 = 3/20
Vậy, 2/5 - 1/4 = 3/20

Câu c)

Đề bài: Tính 3/4 * 2/7

Lời giải:

Nhân hai phân số: 3/4 * 2/7 = (3 * 2) / (4 * 7) = 6/28
Rút gọn phân số: 6/28 = 3/14
Vậy, 3/4 * 2/7 = 3/14

Câu d)

Đề bài: Tính 5/6 : 1/2

Lời giải:

Tìm nghịch đảo của phân số 1/2: Nghịch đảo của 1/2 là 2/1 = 2
Nhân số bị chia với nghịch đảo của số chia: 5/6 * 2 = 10/6
Rút gọn phân số: 10/6 = 5/3
Vậy, 5/6 : 1/2 = 5/3

Mở rộng và Luyện tập

Để hiểu rõ hơn về các phép toán với số hữu tỉ, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 7 tập 1. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến hoặc tham gia các khóa học toán online để nâng cao kiến thức và kỹ năng của mình.

Kết luận

Bài 2 trang 87 sách bài tập Toán 7 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.