Bài 12 Toán lớp 5 thuộc chương trình học Toán 5, tập trung vào việc rèn luyện các kỹ năng giải toán đã học. Tại giaitoan.edu.vn, học sinh có thể tìm thấy lời giải chi tiết, dễ hiểu cho từng bài tập trong sách giáo khoa Bình Minh.
Chúng tôi cung cấp phương pháp giải bài tập một cách logic, giúp các em hiểu sâu sắc kiến thức và tự tin hơn trong quá trình học tập.
Quy đồng mẫu số các phân số sau: <, >, = ? Sắp xếp các phân số sau theo thứ tự từ bé đến lớn: Trường Phổ thông Dân tộc nội trú Vừ A Dính có $frac{3}{{10}}$số học sinh là người dân tộc H’Mông, $frac{1}{2}$ số học sinh là người dân tộc Thái và $frac{1}{5}$ số học sinh là người dân tộc Dao.
Trả lời câu hỏi 4 trang 17 SGK Toán 5 Bình minh
Trường Phổ thông Dân tộc nội trú Vừ A Dính có $\frac{3}{{10}}$số học sinh là người dân tộc H’Mông, $\frac{1}{2}$ số học sinh là người dân tộc Thái và $\frac{1}{5}$ số học sinh là người dân tộc Dao. Hỏi trường đó có số học sinh là người dân tộc nào nhiều nhất?
Phương pháp giải:
- Quy đồng mẫu số các phân số.
- So sánh các phân số để trả lời câu hỏi.
Lời giải chi tiết:
Ta có: $\frac{1}{2} = \frac{{1 \times 5}}{{2 \times 5}} = \frac{5}{{10}}$;$\frac{1}{5} = \frac{{1 \times 2}}{{5 \times 2}} = \frac{2}{{10}}$
Mà $\frac{5}{{10}} > \frac{3}{{10}} > \frac{2}{{10}}$
Vậy trường đó có số học sinh là người dân tộc Thái nhiều nhất.
Trả lời câu hỏi 1 trang 17 SGK Toán 5 Bình minh
Quy đồng mẫu số các phân số sau:
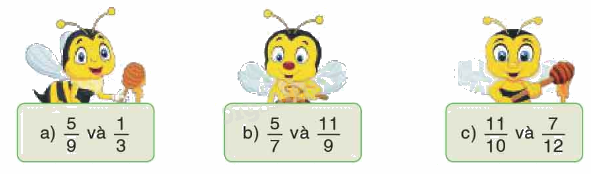
Phương pháp giải:
a) Khi quy đồng mẫu số của hai phân số mà mẫu số lớn chia hết cho mẫu số bé, ta làm như sau:
- Lấy mẫu số lớn hơn là mẫu số chung
- Lấy mẫu số chung chia cho mẫu số bé
- Nhân cả tử số và mẫu số của phân số có mẫu số bé với thương vừa tìm được
b, c) Khi quy đồng mẫu số của hai phân số mà mẫu số này không chia hết cho mẫu số kia, ta làm như sau:
- Chọn mẫu số chung là tích của hai mẫu số đã cho;
- Nhân cả tử số và mẫu số của phân số thứ nhất với mẫu số của phân số thứ hai;
- Nhân cả tử số và mẫu số của phân số thứ hai với mẫu số của phân số thứ nhất;
Ta nhận được hai phân số có cùng mẫu số.
Lời giải chi tiết:
a) Mẫu số chung là 9
$\frac{1}{3} = \frac{{1 \times 3}}{{3 \times 3}} = \frac{3}{9}$; giữ nguyên $\frac{5}{9}$
Quy đồng mẫu số hai phân số $\frac{1}{3}$và $\frac{5}{9}$ ta được $\frac{3}{9}$và $\frac{5}{9}$
b) Mẫu số chung là 63
$\frac{5}{7} = \frac{{5 \times 9}}{{7 \times 9}} = \frac{{45}}{{63}}$; $\frac{{11}}{9} = \frac{{11 \times 7}}{{9 \times 7}} = \frac{{77}}{{63}}$
Quy đồng mẫu số hai phân số $\frac{5}{7}$ và$\frac{{11}}{9}$ ta được $\frac{{45}}{{63}}$ và $\frac{{77}}{{63}}$
c) Mẫu số chung là 10 : 2 × 12 = 60
$\frac{{11}}{{10}} = \frac{{11 \times 6}}{{10 \times 6}} = \frac{{66}}{{60}}$;$\frac{7}{{12}} = \frac{{7 \times 5}}{{12 \times 5}} = \frac{{35}}{{60}}$
Quy đồng mẫu số các phân số $\frac{{11}}{{10}}$ và $\frac{7}{{12}}$ ta được $\frac{{66}}{{60}}$ và $\frac{{35}}{{60}}$
Trả lời câu hỏi 1 trang 17 SGK Toán 5 Bình minh
Quy đồng mẫu số các phân số sau:
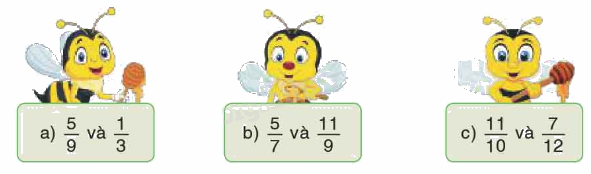
Phương pháp giải:
a) Khi quy đồng mẫu số của hai phân số mà mẫu số lớn chia hết cho mẫu số bé, ta làm như sau:
- Lấy mẫu số lớn hơn là mẫu số chung
- Lấy mẫu số chung chia cho mẫu số bé
- Nhân cả tử số và mẫu số của phân số có mẫu số bé với thương vừa tìm được
b, c) Khi quy đồng mẫu số của hai phân số mà mẫu số này không chia hết cho mẫu số kia, ta làm như sau:
- Chọn mẫu số chung là tích của hai mẫu số đã cho;
- Nhân cả tử số và mẫu số của phân số thứ nhất với mẫu số của phân số thứ hai;
- Nhân cả tử số và mẫu số của phân số thứ hai với mẫu số của phân số thứ nhất;
Ta nhận được hai phân số có cùng mẫu số.
Lời giải chi tiết:
a) Mẫu số chung là 9
$\frac{1}{3} = \frac{{1 \times 3}}{{3 \times 3}} = \frac{3}{9}$; giữ nguyên $\frac{5}{9}$
Quy đồng mẫu số hai phân số $\frac{1}{3}$và $\frac{5}{9}$ ta được $\frac{3}{9}$và $\frac{5}{9}$
b) Mẫu số chung là 63
$\frac{5}{7} = \frac{{5 \times 9}}{{7 \times 9}} = \frac{{45}}{{63}}$; $\frac{{11}}{9} = \frac{{11 \times 7}}{{9 \times 7}} = \frac{{77}}{{63}}$
Quy đồng mẫu số hai phân số $\frac{5}{7}$ và$\frac{{11}}{9}$ ta được $\frac{{45}}{{63}}$ và $\frac{{77}}{{63}}$
c) Mẫu số chung là 10 : 2 × 12 = 60
$\frac{{11}}{{10}} = \frac{{11 \times 6}}{{10 \times 6}} = \frac{{66}}{{60}}$;$\frac{7}{{12}} = \frac{{7 \times 5}}{{12 \times 5}} = \frac{{35}}{{60}}$
Quy đồng mẫu số các phân số $\frac{{11}}{{10}}$ và $\frac{7}{{12}}$ ta được $\frac{{66}}{{60}}$ và $\frac{{35}}{{60}}$
Trả lời câu hỏi 2 trang 17 SGK Toán 5 Bình minh
<, >, = ?
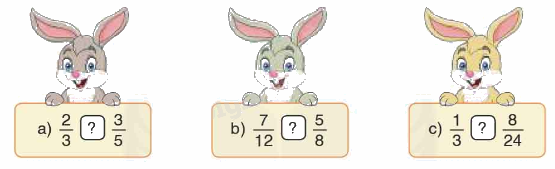
Phương pháp giải:
Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đã cho rồi so sánh hai phân số mới có cùng mẫu số.
Lời giải chi tiết:
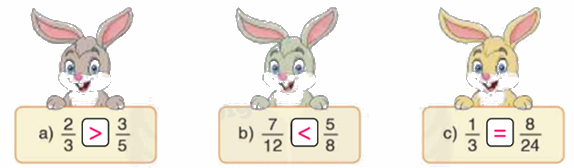
a) Ta có: $\frac{2}{3} = \frac{{10}}{{15}};\frac{3}{5} = \frac{9}{{15}}$
Nên $\frac{2}{3} > \frac{9}{{15}}$
b) Ta có: $\frac{7}{{12}} = \frac{{28}}{{48}};\frac{5}{8} = \frac{{30}}{{48}}$
Nên $\frac{7}{{12}} < \frac{{30}}{{48}}$
c) $\frac{1}{3} = \frac{8}{{24}}$
Trả lời câu hỏi 3 trang 17 SGK Toán 5 Bình minh
Sắp xếp các phân số sau theo thứ tự từ bé đến lớn:

Phương pháp giải:
So sánh các phân số rồi sắp xếp theo thứ tự từ bé đến lớn
Lời giải chi tiết:
a) Ta có: $\frac{5}{2} = \frac{{5 \times 9}}{{2 \times 9}} = \frac{{45}}{{18}}$;$\frac{2}{3} = \frac{{2 \times 6}}{{3 \times 6}} = \frac{{12}}{{18}}$; giữ nguyên $\frac{3}{{18}}$
Mà $\frac{3}{{18}} < \frac{{12}}{{18}} < \frac{{45}}{{18}}$
Vậy các phân số sắp xếp theo thứ tự từ bé đến lớn là: $\frac{3}{{18}};\frac{2}{3};\frac{5}{2}$
b) Ta có: $\frac{5}{4} = \frac{{5 \times 3}}{{4 \times 3}} = \frac{{15}}{{12}}$;$\frac{5}{3} = \frac{{5 \times 4}}{{3 \times 4}} = \frac{{20}}{{12}}$; giữ nguyên $\frac{7}{{12}}$
Mà $\frac{7}{{12}} < \frac{{15}}{{12}} < \frac{{20}}{{12}}$
Vậy các phân số sắp xếp theo thứ tự từ bé đến lớn là: $\frac{7}{{12}};\frac{5}{4};\frac{5}{3}$
Trả lời câu hỏi 4 trang 17 SGK Toán 5 Bình minh
Trường Phổ thông Dân tộc nội trú Vừ A Dính có $\frac{3}{{10}}$số học sinh là người dân tộc H’Mông, $\frac{1}{2}$ số học sinh là người dân tộc Thái và $\frac{1}{5}$ số học sinh là người dân tộc Dao. Hỏi trường đó có số học sinh là người dân tộc nào nhiều nhất?
Phương pháp giải:
- Quy đồng mẫu số các phân số.
- So sánh các phân số để trả lời câu hỏi.
Lời giải chi tiết:
Ta có: $\frac{1}{2} = \frac{{1 \times 5}}{{2 \times 5}} = \frac{5}{{10}}$;$\frac{1}{5} = \frac{{1 \times 2}}{{5 \times 2}} = \frac{2}{{10}}$
Mà $\frac{5}{{10}} > \frac{3}{{10}} > \frac{2}{{10}}$
Vậy trường đó có số học sinh là người dân tộc Thái nhiều nhất.
Trả lời câu hỏi 3 trang 17 SGK Toán 5 Bình minh
Sắp xếp các phân số sau theo thứ tự từ bé đến lớn:

Phương pháp giải:
So sánh các phân số rồi sắp xếp theo thứ tự từ bé đến lớn
Lời giải chi tiết:
a) Ta có: $\frac{5}{2} = \frac{{5 \times 9}}{{2 \times 9}} = \frac{{45}}{{18}}$;$\frac{2}{3} = \frac{{2 \times 6}}{{3 \times 6}} = \frac{{12}}{{18}}$; giữ nguyên $\frac{3}{{18}}$
Mà $\frac{3}{{18}} < \frac{{12}}{{18}} < \frac{{45}}{{18}}$
Vậy các phân số sắp xếp theo thứ tự từ bé đến lớn là: $\frac{3}{{18}};\frac{2}{3};\frac{5}{2}$
b) Ta có: $\frac{5}{4} = \frac{{5 \times 3}}{{4 \times 3}} = \frac{{15}}{{12}}$;$\frac{5}{3} = \frac{{5 \times 4}}{{3 \times 4}} = \frac{{20}}{{12}}$; giữ nguyên $\frac{7}{{12}}$
Mà $\frac{7}{{12}} < \frac{{15}}{{12}} < \frac{{20}}{{12}}$
Vậy các phân số sắp xếp theo thứ tự từ bé đến lớn là: $\frac{7}{{12}};\frac{5}{4};\frac{5}{3}$
Trả lời câu hỏi 2 trang 17 SGK Toán 5 Bình minh
<, >, = ?
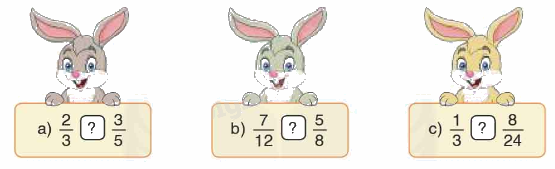
Phương pháp giải:
Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đã cho rồi so sánh hai phân số mới có cùng mẫu số.
Lời giải chi tiết:
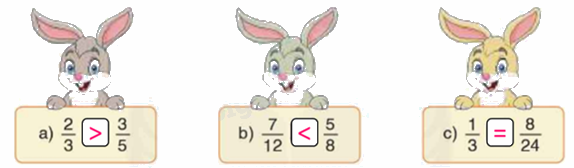
a) Ta có: $\frac{2}{3} = \frac{{10}}{{15}};\frac{3}{5} = \frac{9}{{15}}$
Nên $\frac{2}{3} > \frac{9}{{15}}$
b) Ta có: $\frac{7}{{12}} = \frac{{28}}{{48}};\frac{5}{8} = \frac{{30}}{{48}}$
Nên $\frac{7}{{12}} < \frac{{30}}{{48}}$
c) $\frac{1}{3} = \frac{8}{{24}}$
Bài 12 Toán lớp 5 chương trình SGK Bình Minh là một bài luyện tập quan trọng, giúp củng cố kiến thức về các phép tính với số thập phân, các bài toán có liên quan đến đơn vị đo độ dài, khối lượng, thời gian và giải toán có lời văn. Bài học này yêu cầu học sinh vận dụng linh hoạt các kiến thức đã học để giải quyết các tình huống thực tế.
Bài 12 tập trung vào các dạng bài tập sau:
Để giải các bài tập về phép tính với số thập phân, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số thập phân. Lưu ý khi thực hiện các phép tính, cần đặt các chữ số ở cùng một hàng (dấu phẩy căn chỉnh dấu phẩy). Khi nhân hoặc chia số thập phân, cần bỏ dấu phẩy và thực hiện như phép tính với số tự nhiên, sau đó đặt dấu phẩy ở kết quả cho đúng.
Học sinh cần nhớ các mối quan hệ giữa các đơn vị đo độ dài: 1km = 1000m, 1m = 10dm, 1dm = 10cm, 1cm = 10mm. Khi chuyển đổi đơn vị, cần nhân hoặc chia cho các hệ số tương ứng.
Tương tự như đơn vị đo độ dài, học sinh cần nhớ các mối quan hệ giữa các đơn vị đo khối lượng: 1kg = 1000g, 1yến = 10kg, 1tạ = 100kg, 1tấn = 1000kg.
Học sinh cần nhớ các mối quan hệ giữa các đơn vị đo thời gian: 1giờ = 60phút, 1phút = 60giây. Khi chuyển đổi đơn vị, cần nhân hoặc chia cho các hệ số tương ứng.
Để giải toán có lời văn, học sinh cần:
Bài tập: Một người đi xe đạp từ A đến B với vận tốc 12km/giờ. Hỏi sau 2 giờ người đó đi được bao nhiêu ki-lô-mét?
Giải:
Quãng đường người đó đi được là: 12km/giờ x 2 giờ = 24km
Đáp số: 24km
Để nắm vững kiến thức và kỹ năng giải toán, học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các nguồn tài liệu khác. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập đa dạng, phong phú, giúp học sinh rèn luyện kỹ năng giải toán một cách hiệu quả.
Toán lớp 5 là nền tảng quan trọng cho các môn học ở các lớp trên. Việc học tốt Toán lớp 5 giúp học sinh phát triển tư duy logic, khả năng giải quyết vấn đề và kỹ năng tính toán. Những kỹ năng này rất cần thiết cho sự thành công trong học tập và cuộc sống.
Giaitoan.edu.vn hy vọng với những hướng dẫn chi tiết và bài tập luyện tập phong phú, các em học sinh sẽ học tốt môn Toán lớp 5 và đạt được kết quả cao trong học tập.