Bài học Toán lớp 5 Bài 122 tập trung vào việc giúp học sinh hiểu rõ khái niệm về thể tích hình hộp chữ nhật và cách tính thể tích của hình này. Bài học này thuộc chương trình SGK Bình Minh, cung cấp kiến thức nền tảng quan trọng cho các bài học toán hình học tiếp theo.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để giúp học sinh nắm vững kiến thức và tự tin giải các bài toán liên quan đến thể tích hình hộp chữ nhật.
Tính thể tích của hình hộp chữ nhật có chiều dài bằng a, chiều rộng bằng b và chiều cao bằng c. Biết: Một bể bơi sâu 1,4 m như hình dưới đây. Hỏi cần bao nhiêu mét khối nước để bơm vào bể bơi đó? Biết rằng mặt nước trong bể cách miệng bể 20 cm.
Trả lời câu hỏi 3 trang 50 SGK Toán 5 Bình Minh
Chọn đáp án đúng:
Một thùng đựng hàng dạng hình hộp chữ nhật có chiều dài 2 m, rộng 1,2 m và cao 80 cm. Thể tích của thùng đựng hàng là:
A. 192 m3
B. 256 m3
C. 1,92 m3
D. 19,2 m3
Phương pháp giải:
- Thể tích của thùng đựng hàng = chiều dài × chiều rộng × Chiều cao
Lời giải chi tiết:
Đổi 80 cm = 0,8 m
Thể tích của thùng đựng hàng là:
$2 \times 1,2 \times 0,8 = 1,92$(m3)
Đáp số: 1,92 m3.
Chọn C.
Trả lời câu hỏi 1 trang 50 SGK Toán 5 Bình Minh
Tính thể tích của hình hộp chữ nhật có chiều dài bằng a, chiều rộng bằng b và chiều cao bằng c. Biết:
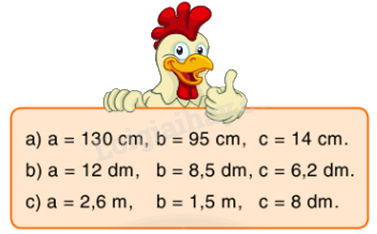
Phương pháp giải:
Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo). $V = a \times b \times c$
Lời giải chi tiết:
a) Thể tích của hình hộp chữ nhật đó là:
\(130 \times 95 \times 14 = 172{\rm{ }}900\)(cm3)
b) Thể tích của hình hộp chữ nhật đó là:
$12 \times 8,5 \times 6,2 = 632,4$(dm3)
c) Đổi: 8dm = 0,8 m
Thể tích của hình hộp chữ nhật đó là:
$2,6 \times 1,5 \times 0,8 = 3,12$(m3)
Trả lời câu hỏi 2 trang 50 SGK Toán 5 Bình Minh
Một bể bơi sâu 1,4 m như hình dưới đây. Hỏi cần bao nhiêu mét khối nước để bơm vào bể bơi đó? Biết rằng mặt nước trong bể cách miệng bể 20 cm.
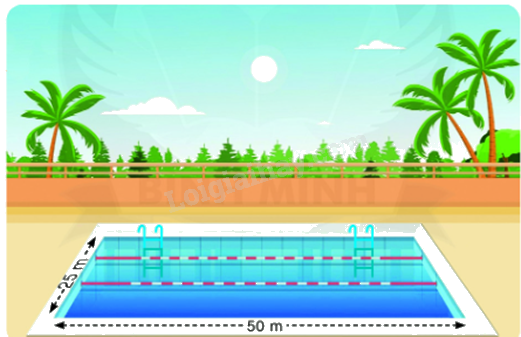
Phương pháp giải:
- Chiều cao khối nước bơm vào bể = chiều sâu của bể - khoảng cách mặt nước với miệng bể
- Số mét khối nước để bơm vào bể bơi = chiều dài × chiều rộng × chiều cao khối nước bơm vào bể
Lời giải chi tiết:
Đổi 20 cm = 0,2 m
Chiều cao khối nước bơm vào bể là:
1,4 – 0,2 = 1,2 (m)
Số mét khối nước để bơm vào bể bơi là:
$50 \times 25 \times 1,2 = 1500$(m3)
Đáp số: 1 500 m3 nước.
Trả lời câu hỏi 1 trang 50 SGK Toán 5 Bình Minh
Tính thể tích của hình hộp chữ nhật có chiều dài bằng a, chiều rộng bằng b và chiều cao bằng c. Biết:
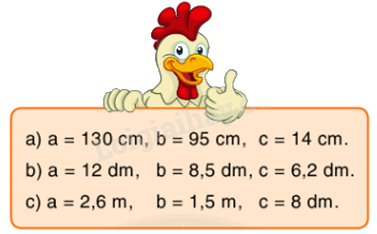
Phương pháp giải:
Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo). $V = a \times b \times c$
Lời giải chi tiết:
a) Thể tích của hình hộp chữ nhật đó là:
\(130 \times 95 \times 14 = 172{\rm{ }}900\)(cm3)
b) Thể tích của hình hộp chữ nhật đó là:
$12 \times 8,5 \times 6,2 = 632,4$(dm3)
c) Đổi: 8dm = 0,8 m
Thể tích của hình hộp chữ nhật đó là:
$2,6 \times 1,5 \times 0,8 = 3,12$(m3)
Trả lời câu hỏi 2 trang 50 SGK Toán 5 Bình Minh
Một bể bơi sâu 1,4 m như hình dưới đây. Hỏi cần bao nhiêu mét khối nước để bơm vào bể bơi đó? Biết rằng mặt nước trong bể cách miệng bể 20 cm.
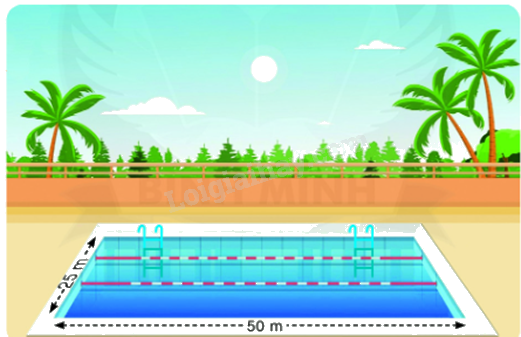
Phương pháp giải:
- Chiều cao khối nước bơm vào bể = chiều sâu của bể - khoảng cách mặt nước với miệng bể
- Số mét khối nước để bơm vào bể bơi = chiều dài × chiều rộng × chiều cao khối nước bơm vào bể
Lời giải chi tiết:
Đổi 20 cm = 0,2 m
Chiều cao khối nước bơm vào bể là:
1,4 – 0,2 = 1,2 (m)
Số mét khối nước để bơm vào bể bơi là:
$50 \times 25 \times 1,2 = 1500$(m3)
Đáp số: 1 500 m3 nước.
Trả lời câu hỏi 3 trang 50 SGK Toán 5 Bình Minh
Chọn đáp án đúng:
Một thùng đựng hàng dạng hình hộp chữ nhật có chiều dài 2 m, rộng 1,2 m và cao 80 cm. Thể tích của thùng đựng hàng là:
A. 192 m3
B. 256 m3
C. 1,92 m3
D. 19,2 m3
Phương pháp giải:
- Thể tích của thùng đựng hàng = chiều dài × chiều rộng × Chiều cao
Lời giải chi tiết:
Đổi 80 cm = 0,8 m
Thể tích của thùng đựng hàng là:
$2 \times 1,2 \times 0,8 = 1,92$(m3)
Đáp số: 1,92 m3.
Chọn C.
Bài 122 Toán lớp 5 thuộc chương trình SGK Bình Minh, giới thiệu về khái niệm thể tích hình hộp chữ nhật và cách tính thể tích của hình này. Đây là một kiến thức cơ bản và quan trọng trong chương trình học Toán lớp 5, giúp học sinh làm quen với các khái niệm hình học không gian và ứng dụng vào giải quyết các bài toán thực tế.
Thể tích của một hình hộp chữ nhật là lượng không gian mà hình đó chiếm giữ. Để hiểu rõ hơn, ta có thể tưởng tượng hình hộp chữ nhật như một chiếc hộp, thể tích của nó chính là lượng nước hoặc vật chất có thể chứa đựng bên trong chiếc hộp đó.
Công thức tính thể tích hình hộp chữ nhật rất đơn giản:
Thể tích = Chiều dài x Chiều rộng x Chiều cao
Trong đó:
Đơn vị đo thể tích thường được sử dụng là mét khối (m3), centimet khối (cm3), đề-xi-mét khối (dm3). Lưu ý rằng:
Ví dụ 1: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Tính thể tích của hình hộp chữ nhật đó.
Giải:
Thể tích của hình hộp chữ nhật là: 5cm x 3cm x 4cm = 60cm3
Ví dụ 2: Một bể nước hình hộp chữ nhật có chiều dài 2m, chiều rộng 1.5m và chiều cao 1m. Tính thể tích của bể nước đó.
Giải:
Thể tích của bể nước là: 2m x 1.5m x 1m = 3m3
Để nắm vững kiến thức về thể tích hình hộp chữ nhật, các em học sinh nên luyện tập thêm các bài tập khác nhau. Các bài tập có thể được tìm thấy trong SGK Toán lớp 5 Bình Minh, các sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Việc tính thể tích hình hộp chữ nhật có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với những kiến thức và ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về thể tích hình hộp chữ nhật và tự tin giải các bài tập liên quan. Chúc các em học tốt!
| Chiều dài | Chiều rộng | Chiều cao | Thể tích |
|---|---|---|---|
| 6cm | 4cm | 2cm | 48cm3 |
| 3m | 2m | 1.5m | 9m3 |