Chào mừng các em học sinh lớp 5 đến với bài học Toán lớp 5 Bài 23. Ôn tập chủ đề 1 - SGK Bình Minh trên giaitoan.edu.vn. Bài học này giúp các em ôn lại kiến thức đã học trong chủ đề 1, chuẩn bị cho các bài học tiếp theo.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Tính Chọn giá trị đúng cho mỗi biểu thức a) Viết mỗi hỗn số sau thành phân số thập phân: Trong ngày Quốc tế Thiếu nhi, một cửa hàng bán đồ chơi đã bán số búp bê bằng $frac{3}{5}$ số siêu nhân và ít hơn số siêu nhân 8 con. Chọn câu trả lời đúng: Bác Hai dựng nước trong hai thùng.
Trả lời câu hỏi 1 trang 30 SGK Toán 5 Bình minh
Tính
a) $\frac{9}{8} + \frac{4}{5}$
b) \(\frac{6}{5} - \frac{5}{{14}}\)
c) $\frac{2}{9} + \frac{1}{6}$
d) \(\frac{5}{6} - \frac{3}{4}\)
Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số đó, rồi cộng (hoặc trừ) hai phân số đã quy đồng.
Lời giải chi tiết:
a) $\frac{9}{8} + \frac{4}{5} = \frac{{45}}{{40}} + \frac{{32}}{{40}} = \frac{{77}}{{40}}$
b) \(\frac{6}{5} - \frac{5}{{14}} = \frac{{84}}{{70}} - \frac{{25}}{{70}} = \frac{{59}}{{70}}\)
c) $\frac{2}{9} + \frac{1}{6} = \frac{4}{{18}} + \frac{3}{{18}} = \frac{7}{{18}}$
d) \(\frac{5}{6} - \frac{3}{4} = \frac{{10}}{{12}} - \frac{9}{{12}} = \frac{1}{{12}}\)
Trả lời câu hỏi 3 trang 30 SGK Toán 5 Bình minh
a) Viết mỗi hỗn số sau thành phân số thập phân:
$63\frac{8}{{10}}$
$5\frac{{26}}{{1000}}$
b) Viết các phân số thập phân sau thành hỗn số:
$\frac{{276}}{{100}}$
$\frac{{7092}}{{1000}}$
Phương pháp giải:
a) Cách chuyển hỗn số thành phân số:
- Tử số của phân số mới bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.
- Mẫu số bằng mẫu số ở phần phân số.
b) Cách chuyển phân số thập phân thành hỗn số:
- Lấy tử số chia cho mẫu số.
- Thương tìm được là phần nguyên; viết phần nguyên kèm theo một phân số có tử số là số dư, mẫu số là số chia.
Lời giải chi tiết:
a)
$63\frac{8}{{10}} = \frac{{63 \times 10 + 8}}{{10}} = \frac{{638}}{{10}}$
$5\frac{{26}}{{1000}} = \frac{{5 \times 1000 + 26}}{{1000}} = \frac{{5026}}{{1000}}$
b) Ta có: 276 : 100 = 2 (dư 76)
Vậy:
$\frac{{276}}{{100}} = 2\frac{{76}}{{100}}$
Ta có: 7 092 : 1 000 = 7 (dư 92)
$\frac{{7092}}{{1000}} = 7\frac{{92}}{{1000}}$
Trả lời câu hỏi 4 trang 30 SGK Toán 5 Bình minh
Trong ngày Quốc tế Thiếu nhi, một cửa hàng bán đồ chơi đã bán số búp bê bằng $\frac{3}{5}$ số siêu nhân và ít hơn số siêu nhân 8 con. Tìm số búp bê và số siêu nhân đã bán.
Phương pháp giải:
- Vẽ sơ đồ.
- Tìm số búp bê và số siêu nhân đã bán theo bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
Lời giải chi tiết:
Ta có sơ đồ:
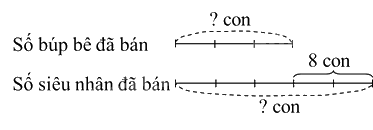
Theo sơ đồ, hiệu số phần bằng nhau là:
5 – 3 = 2 (phần)
Số búp bê đã bán là
8 : 2 x 3 = 12 (con)
Số siêu nhân đã bán là:
12 + 8 = 20 (con)
Đáp số: Búp bê: 12 con ; Siêu nhân: 20 con.
Trả lời câu hỏi 5 trang 30 SGK Toán 5 Bình minh
Chọn câu trả lời đúng:
Bác Hai dựng nước trong hai thùng. Lượng nước chứa trong thùng thứ nhất bằng $\frac{5}{3}$ lượng nước trong thùng thứ hai. Sau khi chia đều lượng nước đó ở cả hai thùng thì mỗi thùng đều chứa 160 l nước. Vậy lúc đầu:
A. Thùng thứ nhất chứa 60 l nước và thùng thứ hai chứa 100 l nước.
B. Thùng thứ nhất chứa 200 l nước và thùng thứ hai chứa 120 l nước.
C. Thùng thứ nhất chứa 120 l nước và thùng thứ hai chứa 200 l nước.
D. Thùng thứ nhất chứa 100 l nước và thùng thứ hai chứa 60 l nước.
Phương pháp giải:
- Tổng số lít nước ở hai thùng lúc đầu = Tổng số lít nước ở hai thùng lúc sau.
- Đưa về bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Lời giải chi tiết:
Tóm tắt
Lượng nước trong thùng thứ nhất: $\frac{5}{3}$ lượng nước trong thùng thứ hai
Sau khi chia đều, mỗi thùng chứa: 160 l nước
Ban đầu thùng thứ nhất: ? l nước
Thùng thứ hai: ? l nước
Bài giải
Vì khi chia đều lượng nước ở cả hai thùng nên tổng số lít nước ở hai thùng lúc đầu bằng tổng số lít nước ở hai thùng lúc sau.
Tổng số lít nước ở hai thùng lúc đầu là:
160 + 160 = 320 (lít)
Ta có sơ đồ:
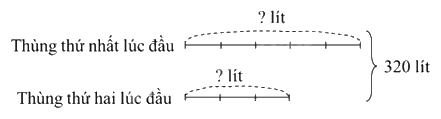
Theo sơ đồ, tổng số phần bằng nhau là:
5 + 3 = 8 (phần)
Lúc đầu thùng thứ nhất chứa số lít nước là:
320 : 8 x 5 = 200 (lít)
Lúc đầu thùng thứ hai chứa số lít nước là:
320 – 200 = 120 (lít)
Đáp số: Thùng thứ nhất: 200 l nước;
Thùng thứ hai: 120 l nước.
Chọn B.
Trả lời câu hỏi 2 trang 30 SGK Toán 5 Bình minh
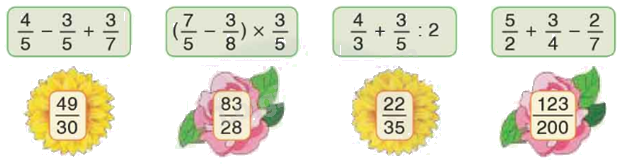
Chọn giá trị đúng cho mỗi biểu thức
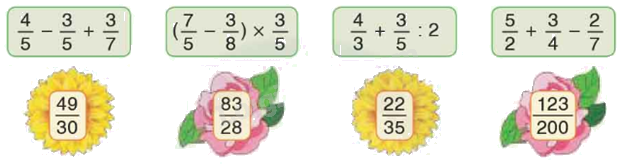
Phương pháp giải:
Thứ tự thực hiện phép tính:
- Khi thực hiện các phép tính trong biểu thức, ta thực hiện từ trái qua phải.
- Nếu biểu thức có dấu ngoặc, ta thực hiện các phép toán trong ngoặc trước.
- Nếu biểu thức gồm các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép toán nhân, chia trước sau đó mới đến phép toán cộng, trừ.
Lời giải chi tiết:
Ta có:
\(\frac{4}{5} - \frac{3}{5} + \frac{3}{7} = \frac{1}{5} + \frac{3}{7} = \frac{7}{{35}} + \frac{{15}}{{35}} = \frac{{22}}{{35}}\)
\(\left( {\frac{7}{5} - \frac{3}{8}} \right) \times \frac{3}{5} = \left( {\frac{{56}}{{40}} - \frac{{15}}{{40}}} \right) \times \frac{3}{5} = \frac{{41}}{{40}} \times \frac{3}{5} = \frac{{123}}{{200}}\)
\(\frac{4}{3} + \frac{3}{5}:2 = \frac{4}{3} + \frac{3}{5} \times \frac{1}{2} = \frac{4}{3} + \frac{3}{{10}} = \frac{{40}}{{30}} + \frac{9}{{30}} = \frac{{49}}{{30}}\)
\(\frac{5}{2} + \frac{3}{4} - \frac{2}{7} = \frac{{70}}{{28}} + \frac{{21}}{{28}} - \frac{8}{{28}} = \frac{{83}}{{28}}\)
Vậy:
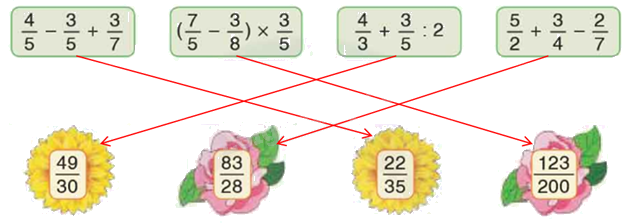
Trả lời câu hỏi 1 trang 30 SGK Toán 5 Bình minh
Tính
a) $\frac{9}{8} + \frac{4}{5}$
b) \(\frac{6}{5} - \frac{5}{{14}}\)
c) $\frac{2}{9} + \frac{1}{6}$
d) \(\frac{5}{6} - \frac{3}{4}\)
Phương pháp giải:
Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số đó, rồi cộng (hoặc trừ) hai phân số đã quy đồng.
Lời giải chi tiết:
a) $\frac{9}{8} + \frac{4}{5} = \frac{{45}}{{40}} + \frac{{32}}{{40}} = \frac{{77}}{{40}}$
b) \(\frac{6}{5} - \frac{5}{{14}} = \frac{{84}}{{70}} - \frac{{25}}{{70}} = \frac{{59}}{{70}}\)
c) $\frac{2}{9} + \frac{1}{6} = \frac{4}{{18}} + \frac{3}{{18}} = \frac{7}{{18}}$
d) \(\frac{5}{6} - \frac{3}{4} = \frac{{10}}{{12}} - \frac{9}{{12}} = \frac{1}{{12}}\)
Trả lời câu hỏi 2 trang 30 SGK Toán 5 Bình minh
Chọn giá trị đúng cho mỗi biểu thức
Phương pháp giải:
Thứ tự thực hiện phép tính:
- Khi thực hiện các phép tính trong biểu thức, ta thực hiện từ trái qua phải.
- Nếu biểu thức có dấu ngoặc, ta thực hiện các phép toán trong ngoặc trước.
- Nếu biểu thức gồm các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép toán nhân, chia trước sau đó mới đến phép toán cộng, trừ.
Lời giải chi tiết:
Ta có:
\(\frac{4}{5} - \frac{3}{5} + \frac{3}{7} = \frac{1}{5} + \frac{3}{7} = \frac{7}{{35}} + \frac{{15}}{{35}} = \frac{{22}}{{35}}\)
\(\left( {\frac{7}{5} - \frac{3}{8}} \right) \times \frac{3}{5} = \left( {\frac{{56}}{{40}} - \frac{{15}}{{40}}} \right) \times \frac{3}{5} = \frac{{41}}{{40}} \times \frac{3}{5} = \frac{{123}}{{200}}\)
\(\frac{4}{3} + \frac{3}{5}:2 = \frac{4}{3} + \frac{3}{5} \times \frac{1}{2} = \frac{4}{3} + \frac{3}{{10}} = \frac{{40}}{{30}} + \frac{9}{{30}} = \frac{{49}}{{30}}\)
\(\frac{5}{2} + \frac{3}{4} - \frac{2}{7} = \frac{{70}}{{28}} + \frac{{21}}{{28}} - \frac{8}{{28}} = \frac{{83}}{{28}}\)
Vậy:
Trả lời câu hỏi 3 trang 30 SGK Toán 5 Bình minh
a) Viết mỗi hỗn số sau thành phân số thập phân:
$63\frac{8}{{10}}$
$5\frac{{26}}{{1000}}$
b) Viết các phân số thập phân sau thành hỗn số:
$\frac{{276}}{{100}}$
$\frac{{7092}}{{1000}}$
Phương pháp giải:
a) Cách chuyển hỗn số thành phân số:
- Tử số của phân số mới bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.
- Mẫu số bằng mẫu số ở phần phân số.
b) Cách chuyển phân số thập phân thành hỗn số:
- Lấy tử số chia cho mẫu số.
- Thương tìm được là phần nguyên; viết phần nguyên kèm theo một phân số có tử số là số dư, mẫu số là số chia.
Lời giải chi tiết:
a)
$63\frac{8}{{10}} = \frac{{63 \times 10 + 8}}{{10}} = \frac{{638}}{{10}}$
$5\frac{{26}}{{1000}} = \frac{{5 \times 1000 + 26}}{{1000}} = \frac{{5026}}{{1000}}$
b) Ta có: 276 : 100 = 2 (dư 76)
Vậy:
$\frac{{276}}{{100}} = 2\frac{{76}}{{100}}$
Ta có: 7 092 : 1 000 = 7 (dư 92)
$\frac{{7092}}{{1000}} = 7\frac{{92}}{{1000}}$
Trả lời câu hỏi 4 trang 30 SGK Toán 5 Bình minh
Trong ngày Quốc tế Thiếu nhi, một cửa hàng bán đồ chơi đã bán số búp bê bằng $\frac{3}{5}$ số siêu nhân và ít hơn số siêu nhân 8 con. Tìm số búp bê và số siêu nhân đã bán.
Phương pháp giải:
- Vẽ sơ đồ.
- Tìm số búp bê và số siêu nhân đã bán theo bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó.
Lời giải chi tiết:
Ta có sơ đồ:
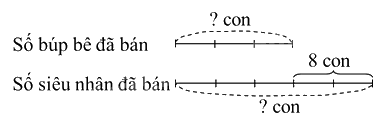
Theo sơ đồ, hiệu số phần bằng nhau là:
5 – 3 = 2 (phần)
Số búp bê đã bán là
8 : 2 x 3 = 12 (con)
Số siêu nhân đã bán là:
12 + 8 = 20 (con)
Đáp số: Búp bê: 12 con ; Siêu nhân: 20 con.
Trả lời câu hỏi 5 trang 30 SGK Toán 5 Bình minh
Chọn câu trả lời đúng:
Bác Hai dựng nước trong hai thùng. Lượng nước chứa trong thùng thứ nhất bằng $\frac{5}{3}$ lượng nước trong thùng thứ hai. Sau khi chia đều lượng nước đó ở cả hai thùng thì mỗi thùng đều chứa 160 l nước. Vậy lúc đầu:
A. Thùng thứ nhất chứa 60 l nước và thùng thứ hai chứa 100 l nước.
B. Thùng thứ nhất chứa 200 l nước và thùng thứ hai chứa 120 l nước.
C. Thùng thứ nhất chứa 120 l nước và thùng thứ hai chứa 200 l nước.
D. Thùng thứ nhất chứa 100 l nước và thùng thứ hai chứa 60 l nước.
Phương pháp giải:
- Tổng số lít nước ở hai thùng lúc đầu = Tổng số lít nước ở hai thùng lúc sau.
- Đưa về bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
Lời giải chi tiết:
Tóm tắt
Lượng nước trong thùng thứ nhất: $\frac{5}{3}$ lượng nước trong thùng thứ hai
Sau khi chia đều, mỗi thùng chứa: 160 l nước
Ban đầu thùng thứ nhất: ? l nước
Thùng thứ hai: ? l nước
Bài giải
Vì khi chia đều lượng nước ở cả hai thùng nên tổng số lít nước ở hai thùng lúc đầu bằng tổng số lít nước ở hai thùng lúc sau.
Tổng số lít nước ở hai thùng lúc đầu là:
160 + 160 = 320 (lít)
Ta có sơ đồ:
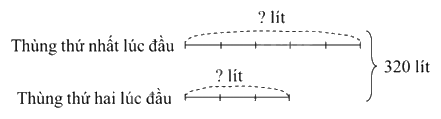
Theo sơ đồ, tổng số phần bằng nhau là:
5 + 3 = 8 (phần)
Lúc đầu thùng thứ nhất chứa số lít nước là:
320 : 8 x 5 = 200 (lít)
Lúc đầu thùng thứ hai chứa số lít nước là:
320 – 200 = 120 (lít)
Đáp số: Thùng thứ nhất: 200 l nước;
Thùng thứ hai: 120 l nước.
Chọn B.
Bài 23 Toán lớp 5 thuộc chương trình ôn tập chủ đề 1, là cơ hội để học sinh củng cố lại những kiến thức đã học về các phép tính với số tự nhiên, các bài toán có liên quan đến đơn vị đo độ dài, khối lượng, thời gian và các bài toán giải đơn giản. Bài học này đóng vai trò quan trọng trong việc xây dựng nền tảng toán học vững chắc cho các em.
Bài 23 gồm các bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết. Dưới đây là một số dạng bài tập thường gặp:
Các bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia với số tự nhiên. Để giải các bài tập này, học sinh cần nắm vững các quy tắc thực hiện các phép tính và tính toán chính xác.
Ví dụ: Tính 1234 + 5678 = ?
Giải: 1234 + 5678 = 6912
Các bài tập này yêu cầu học sinh đổi đơn vị đo độ dài, khối lượng, thời gian và thực hiện các phép tính với các đơn vị đo này. Để giải các bài tập này, học sinh cần nắm vững các mối quan hệ giữa các đơn vị đo và thực hiện các phép tính chính xác.
Ví dụ: Đổi 3km ra mét?
Giải: 1km = 1000m => 3km = 3 x 1000 = 3000m
Các bài tập này yêu cầu học sinh giải các bài toán đơn giản, thường gặp trong cuộc sống. Để giải các bài tập này, học sinh cần đọc kỹ đề bài, xác định được các yếu tố đã cho và yếu tố cần tìm, sau đó vận dụng kiến thức đã học để giải quyết.
Ví dụ: Một cửa hàng có 25kg gạo. Người ta đã bán được 12kg gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Giải: Số gạo còn lại là: 25 - 12 = 13 (kg)
Giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập trong Bài 23 Toán lớp 5. Các lời giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin giải các bài tập tương tự.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể làm thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online.
Bài 23 Toán lớp 5 là một bài học quan trọng, giúp học sinh ôn tập lại kiến thức đã học và chuẩn bị cho các bài học tiếp theo. Hy vọng với sự hướng dẫn chi tiết của giaitoan.edu.vn, các em sẽ học tập tốt và đạt kết quả cao trong môn Toán.
| Đơn vị đo độ dài | Đơn vị đo khối lượng | Đơn vị đo thời gian |
|---|---|---|
| 1km = 1000m | 1kg = 1000g | 1 giờ = 60 phút |
| 1m = 100cm | 1 tấn = 1000kg | 1 phút = 60 giây |