Bài 6 Toán lớp 5 thuộc chương trình ôn tập về phân số, tiếp tục củng cố kiến thức và kỹ năng giải toán liên quan đến các phép toán với phân số. Bài học này giúp học sinh nắm vững các quy tắc và áp dụng vào giải các bài tập thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK Bình Minh, giúp học sinh tự học hiệu quả và đạt kết quả tốt nhất.
Quy đồng mẫu số các phân số sau: Rút gọn các phân số sau để được phân số tối giản: <, >, = ? Viết các phân số sau theo thứ tự từ bé đến lớn: Trong dịp tết Trung thu, mỗi bạn An, Cường, Hoa đều được tặng một cái bánh như nhau.
Trả lời câu hỏi 1 trang 11 SGK Toán 5 Bình minh
Quy đồng mẫu số các phân số sau:
a) $\frac{6}{5}$ và $\frac{{12}}{{30}}$
b) $\frac{5}{8}$ và $\frac{7}{{16}}$
c) $\frac{3}{4}$; $\frac{5}{{12}}$ và $\frac{7}{6}$
Phương pháp giải:
Khi quy đồng mẫu số của hai phân số mà mẫu số lớn chia hết cho mẫu số bé, ta làm như sau:
- Lấy mẫu số lớn hơn là mẫu số chung
- Lấy mẫu số chung chia cho mẫu số bé
- Nhân cả tử số và mẫu số của phân số có mẫu số bé với thương vừa tìm được
Lời giải chi tiết:
a) Mẫu số chung là 30
$\frac{6}{5} = \frac{{6 \times 6}}{{5 \times 6}} = \frac{{36}}{{30}}$, giữ nguyên $\frac{{12}}{{30}}$
Quy đồng mẫu số hai phân số $\frac{6}{5}$ và $\frac{{12}}{{30}}$ta được $\frac{{36}}{{30}}$và $\frac{{12}}{{30}}$
b) Mẫu số chung là 16
$\frac{5}{8} = \frac{{5 \times 2}}{{8 \times 2}} = \frac{{10}}{{16}}$, giữ nguyên $\frac{7}{{16}}$
Quy đồng mẫu số hai phân số $\frac{5}{8}$ và ta được $\frac{{10}}{{16}}$ và $\frac{7}{{16}}$
c) Mẫu số chung là 12
$\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$, $\frac{7}{6} = \frac{{7 \times 2}}{{6 \times 2}} = \frac{{14}}{{12}}$, giữ nguyên $\frac{5}{{12}}$
Quy đồng mẫu số các phân số $\frac{3}{4}$; $\frac{5}{{12}}$và $\frac{7}{6}$ta được $\frac{9}{{12}}$;$\frac{5}{{12}}$và $\frac{{14}}{{12}}$
Trả lời câu hỏi 2 trang 11 SGK Toán 5 Bình minh
Rút gọn các phân số sau để được phân số tối giản:
$\frac{{20}}{{25}}$; $\frac{{24}}{{36}}$; $\frac{{35}}{{14}}$; $\frac{{36}}{{64}}$
Phương pháp giải:
Khi rút gọn phân số ta có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia cả tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
$\frac{{20}}{{25}} = \frac{{20:5}}{{25:5}} = \frac{4}{5}$
$\frac{{24}}{{36}} = \frac{{24:12}}{{36:12}} = \frac{2}{3}$
$\frac{{35}}{{14}} = \frac{{35:7}}{{14:7}} = \frac{5}{2}$
$\frac{{36}}{{64}} = \frac{{36:4}}{{64:4}} = \frac{9}{{16}}$
Trả lời câu hỏi 5 trang 11 SGK Toán 5 Bình minh
Trong dịp tết Trung thu, mỗi bạn An, Cường, Hoa đều được tặng một cái bánh như nhau. An ăn hết $\frac{2}{3}$cái bánh, Cường ăn hết $\frac{3}{4}$cái bánh còn Hoa ăn hết $\frac{8}{{12}}$cái bánh. Hỏi bạn nào ăn nhiều nhất?
Phương pháp giải:
- Quy đồng mẫu số các phân số.
- So sánh các phân số để trả lời câu hỏi.
Lời giải chi tiết:
Ta có: $\frac{2}{3} = \frac{{2 \times 4}}{{3 \times 4}} = \frac{8}{{12}}$; $\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$
Mà $\frac{8}{{12}} < \frac{9}{{12}}$
Vậy bạn Cường ăn nhiều nhất.
Trả lời câu hỏi 4 trang 11 SGK Toán 5 Bình minh
Viết các phân số sau theo thứ tự từ bé đến lớn:
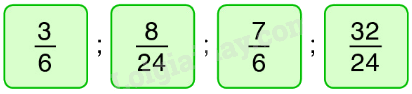
Phương pháp giải:
So sánh các phân số rồi sắp xếp theo thứ tự từ bé đến lớn.
Lời giải chi tiết:
Ta có: $\frac{8}{{24}} = \frac{{8:4}}{{24:4}} = \frac{2}{6}$, $\frac{{32}}{{24}} = \frac{{32:4}}{{24:4}} = \frac{8}{6}$
Mà $\frac{2}{6}$ < $\frac{3}{6}$ < $\frac{7}{6}$ < $\frac{8}{6}$
Vậy các phân số viết theo thứ tự từ bé đến lớn là: $\frac{8}{{24}};\frac{3}{6};\frac{7}{6};\frac{{32}}{{24}}$
Trả lời câu hỏi 3 trang 11 SGK Toán 5 Bình minh
<, >, = ?
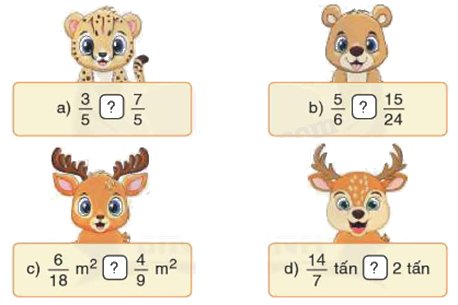
Phương pháp giải:
- Trong hai phân số có cùng mẫu số, phân số nào có tử số bé hơn thì bé hơn.
- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đã cho rồi so sánh hai phân số mới có cùng mẫu số.
Lời giải chi tiết:
a) Vì 3 < 7 nên $\frac{3}{5} < \frac{7}{5}$
b) $\frac{{15}}{{24}} = \frac{{15:3}}{{24:3}} = \frac{5}{8}$
Ta so sánh $\frac{5}{6}$ và $\frac{5}{8}$. Vì 6 < 8 nên $\frac{5}{6}$ > $\frac{5}{8}$ hay $\frac{5}{6}$ > $\frac{{15}}{{24}}$
c) $\frac{6}{{18}} = \frac{3}{9}$. $\frac{3}{9}$ < $\frac{4}{9}$ nên $\frac{6}{{18}}$m2 < $\frac{4}{9}$ m2
d) $\frac{{14}}{7} = 2$ nên $\frac{{14}}{7}$ tấn = 2 tấn
Trả lời câu hỏi 1 trang 11 SGK Toán 5 Bình minh
Quy đồng mẫu số các phân số sau:
a) $\frac{6}{5}$ và $\frac{{12}}{{30}}$
b) $\frac{5}{8}$ và $\frac{7}{{16}}$
c) $\frac{3}{4}$; $\frac{5}{{12}}$ và $\frac{7}{6}$
Phương pháp giải:
Khi quy đồng mẫu số của hai phân số mà mẫu số lớn chia hết cho mẫu số bé, ta làm như sau:
- Lấy mẫu số lớn hơn là mẫu số chung
- Lấy mẫu số chung chia cho mẫu số bé
- Nhân cả tử số và mẫu số của phân số có mẫu số bé với thương vừa tìm được
Lời giải chi tiết:
a) Mẫu số chung là 30
$\frac{6}{5} = \frac{{6 \times 6}}{{5 \times 6}} = \frac{{36}}{{30}}$, giữ nguyên $\frac{{12}}{{30}}$
Quy đồng mẫu số hai phân số $\frac{6}{5}$ và $\frac{{12}}{{30}}$ta được $\frac{{36}}{{30}}$và $\frac{{12}}{{30}}$
b) Mẫu số chung là 16
$\frac{5}{8} = \frac{{5 \times 2}}{{8 \times 2}} = \frac{{10}}{{16}}$, giữ nguyên $\frac{7}{{16}}$
Quy đồng mẫu số hai phân số $\frac{5}{8}$ và ta được $\frac{{10}}{{16}}$ và $\frac{7}{{16}}$
c) Mẫu số chung là 12
$\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$, $\frac{7}{6} = \frac{{7 \times 2}}{{6 \times 2}} = \frac{{14}}{{12}}$, giữ nguyên $\frac{5}{{12}}$
Quy đồng mẫu số các phân số $\frac{3}{4}$; $\frac{5}{{12}}$và $\frac{7}{6}$ta được $\frac{9}{{12}}$;$\frac{5}{{12}}$và $\frac{{14}}{{12}}$
Trả lời câu hỏi 2 trang 11 SGK Toán 5 Bình minh
Rút gọn các phân số sau để được phân số tối giản:
$\frac{{20}}{{25}}$; $\frac{{24}}{{36}}$; $\frac{{35}}{{14}}$; $\frac{{36}}{{64}}$
Phương pháp giải:
Khi rút gọn phân số ta có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia cả tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
$\frac{{20}}{{25}} = \frac{{20:5}}{{25:5}} = \frac{4}{5}$
$\frac{{24}}{{36}} = \frac{{24:12}}{{36:12}} = \frac{2}{3}$
$\frac{{35}}{{14}} = \frac{{35:7}}{{14:7}} = \frac{5}{2}$
$\frac{{36}}{{64}} = \frac{{36:4}}{{64:4}} = \frac{9}{{16}}$
Trả lời câu hỏi 3 trang 11 SGK Toán 5 Bình minh
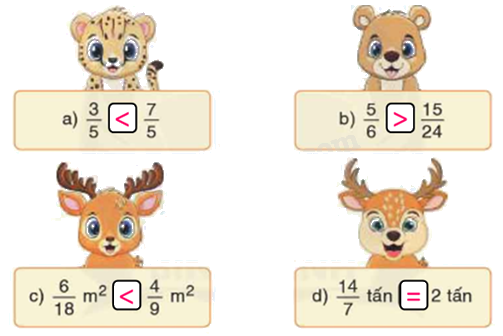
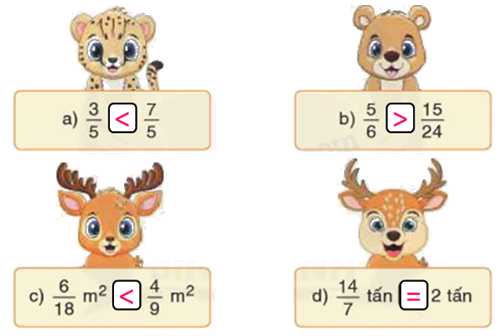
<, >, = ?
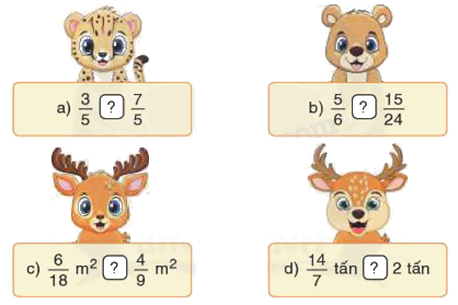
Phương pháp giải:
- Trong hai phân số có cùng mẫu số, phân số nào có tử số bé hơn thì bé hơn.
- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đã cho rồi so sánh hai phân số mới có cùng mẫu số.
Lời giải chi tiết:
a) Vì 3 < 7 nên $\frac{3}{5} < \frac{7}{5}$
b) $\frac{{15}}{{24}} = \frac{{15:3}}{{24:3}} = \frac{5}{8}$
Ta so sánh $\frac{5}{6}$ và $\frac{5}{8}$. Vì 6 < 8 nên $\frac{5}{6}$ > $\frac{5}{8}$ hay $\frac{5}{6}$ > $\frac{{15}}{{24}}$
c) $\frac{6}{{18}} = \frac{3}{9}$. $\frac{3}{9}$ < $\frac{4}{9}$ nên $\frac{6}{{18}}$m2 < $\frac{4}{9}$ m2
d) $\frac{{14}}{7} = 2$ nên $\frac{{14}}{7}$ tấn = 2 tấn
Trả lời câu hỏi 4 trang 11 SGK Toán 5 Bình minh
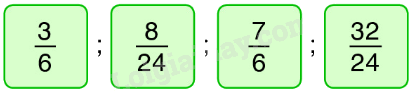
Viết các phân số sau theo thứ tự từ bé đến lớn:
Phương pháp giải:
So sánh các phân số rồi sắp xếp theo thứ tự từ bé đến lớn.
Lời giải chi tiết:
Ta có: $\frac{8}{{24}} = \frac{{8:4}}{{24:4}} = \frac{2}{6}$, $\frac{{32}}{{24}} = \frac{{32:4}}{{24:4}} = \frac{8}{6}$
Mà $\frac{2}{6}$ < $\frac{3}{6}$ < $\frac{7}{6}$ < $\frac{8}{6}$
Vậy các phân số viết theo thứ tự từ bé đến lớn là: $\frac{8}{{24}};\frac{3}{6};\frac{7}{6};\frac{{32}}{{24}}$
Trả lời câu hỏi 5 trang 11 SGK Toán 5 Bình minh
Trong dịp tết Trung thu, mỗi bạn An, Cường, Hoa đều được tặng một cái bánh như nhau. An ăn hết $\frac{2}{3}$cái bánh, Cường ăn hết $\frac{3}{4}$cái bánh còn Hoa ăn hết $\frac{8}{{12}}$cái bánh. Hỏi bạn nào ăn nhiều nhất?
Phương pháp giải:
- Quy đồng mẫu số các phân số.
- So sánh các phân số để trả lời câu hỏi.
Lời giải chi tiết:
Ta có: $\frac{2}{3} = \frac{{2 \times 4}}{{3 \times 4}} = \frac{8}{{12}}$; $\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$
Mà $\frac{8}{{12}} < \frac{9}{{12}}$
Vậy bạn Cường ăn nhiều nhất.
Bài 6 Toán lớp 5 tiếp tục chương trình ôn tập về phân số, đi sâu vào việc củng cố các kiến thức đã học và rèn luyện kỹ năng giải toán. Bài học này tập trung vào việc vận dụng các phép toán cộng, trừ, nhân, chia phân số trong các tình huống khác nhau.
I. Mục tiêu bài học
II. Nội dung bài học
Bài 6 Ôn tập về phân số (tiếp theo) bao gồm các nội dung chính sau:
III. Giải chi tiết bài tập
Dưới đây là giải chi tiết các bài tập trong SGK Bình Minh:
Bài 1: Tính
a) 2/5 + 3/5 = ?
Giải: 2/5 + 3/5 = (2+3)/5 = 5/5 = 1
b) 7/8 - 1/8 = ?
Giải: 7/8 - 1/8 = (7-1)/8 = 6/8 = 3/4
c) 1/2 x 3/4 = ?
Giải: 1/2 x 3/4 = (1x3)/(2x4) = 3/8
d) 2/3 : 1/2 = ?
Giải: 2/3 : 1/2 = 2/3 x 2/1 = 4/3
Bài 2: Tính
a) (1/2 + 1/3) x 6 = ?
Giải: (1/2 + 1/3) x 6 = (3/6 + 2/6) x 6 = 5/6 x 6 = 5
b) (2/5 - 1/5) : 1/4 = ?
Giải: (2/5 - 1/5) : 1/4 = 1/5 : 1/4 = 1/5 x 4/1 = 4/5
Bài 3: Một cửa hàng có 45 kg gạo. Buổi sáng bán được 2/5 số gạo, buổi chiều bán được 1/3 số gạo còn lại. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Giải:
Số gạo bán được buổi sáng là: 45 x 2/5 = 18 kg
Số gạo còn lại sau buổi sáng là: 45 - 18 = 27 kg
Số gạo bán được buổi chiều là: 27 x 1/3 = 9 kg
Số gạo còn lại sau buổi chiều là: 27 - 9 = 18 kg
Đáp số: 18 kg
Bài 4: Một hình chữ nhật có chiều dài 5/4 m, chiều rộng 2/3 m. Tính diện tích hình chữ nhật đó.
Giải:
Diện tích hình chữ nhật là: (5/4) x (2/3) = 10/12 = 5/6 m2
Đáp số: 5/6 m2
IV. Luyện tập thêm
Để củng cố kiến thức và kỹ năng giải toán về phân số, các em có thể tự luyện tập thêm các bài tập sau:
V. Kết luận
Bài 6 Toán lớp 5 Ôn tập về phân số (tiếp theo) là một bài học quan trọng giúp học sinh củng cố kiến thức và kỹ năng giải toán về phân số. Việc nắm vững các quy tắc và áp dụng vào giải các bài tập thực tế sẽ giúp học sinh tự tin hơn trong học tập và đạt kết quả tốt nhất.
Hy vọng với lời giải chi tiết và các bài tập luyện tập, các em học sinh sẽ học tốt môn Toán lớp 5!