Chào mừng các em học sinh lớp 4 đến với bài học Toán lớp 4 trang 18 - Bài 100: Luyện tập thuộc sách giáo khoa Toán 4 - SGK Bình Minh. Bài học này giúp các em củng cố kiến thức đã học về các phép tính và ứng dụng vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong sách, giúp các em tự tin hơn trong quá trình học tập và làm bài.
Quy đồng mẫu số các phân số sau
a) Viết 3 và $\frac{2}{3}$ thành hai phân số đều có mẫu số là 3
b) Viết $\frac{2}{3}$ ; 5 và $\frac{7}{{12}}$ thành ba phân số đều có mẫu số bằng 12.
Phương pháp giải:
- Lấy mẫu số chung chia cho mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
Lời giải chi tiết:
a) $3 = \frac{9}{3}$ ; giữ nguyên $\frac{2}{3}$
b) $\frac{2}{3} = \frac{8}{{12}}$ ; $5 = \frac{{60}}{{12}}$ ; giữ nguyên $\frac{7}{{12}}$
Số?
Ba đội vận tải được giao vận chuyển một lô hàng. Đội Một vận chuyển được $\frac{1}{7}$ lô hàng, đội Hai vận chuyển được $\frac{4}{{21}}$ lô hàng và đội Ba vận chuyển được $\frac{2}{3}$ lô hàng. Vậy:
a) Đội Một vận chuyển được $\frac{?}{{21}}$ lô hàng.
b) Đội Ba vận chuyển được $\frac{?}{{21}}$ lô hàng.
Phương pháp giải:
a) Quy đồng phân số $\frac{1}{7}$ với mẫu số chung là 21
b) Quy đồng phân số $\frac{2}{3}$ với mẫu số chung là 21
Lời giải chi tiết:
a) Ta có $\frac{1}{7} = \frac{3}{{21}}$. Đội Một vận chuyển được $\frac{3}{{21}}$ lô hàng.
b) Ta có $\frac{2}{3} = \frac{{14}}{{21}}$. Đội Ba vận chuyển được $\frac{{14}}{{21}}$ lô hàng.
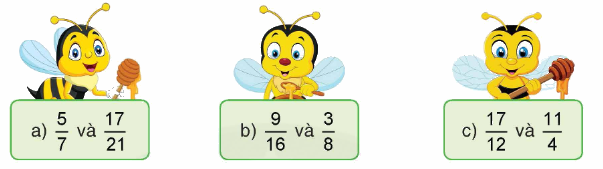
Quy đồng mẫu số các phân số sau:
Phương pháp giải:
Khi quy đồng mẫu số của hai phân số mà mẫu số lớn chia hết cho mẫu số bé, ta làm như sau:
- Lấy mẫu số lớn hơn là mẫu số chung
- Lấy mẫu số chung chia cho mẫu số bé
- Nhân cả tử số và mẫu số của phân số có mẫu số bé với thương vừa tìm được
Lời giải chi tiết:
a) Mẫu số chung là 21
$\frac{5}{7} = \frac{{5 \times 3}}{{7 \times 3}} = \frac{{15}}{{21}}$, giữ nguyên $\frac{{17}}{{21}}$
Quy đồng mẫu số hai phân số $\frac{5}{7}$ và $\frac{{17}}{{21}}$ ta được $\frac{{15}}{{21}}$ và $\frac{{17}}{{21}}$
b) Mẫu số chung là 16
$\frac{3}{8} = \frac{{3 \times 2}}{{8 \times 2}} = \frac{6}{{16}}$
Quy đồng mẫu số hai phân số $\frac{9}{{16}}$ và $\frac{3}{8}$ ta được $\frac{9}{{16}}$ và $\frac{6}{{16}}$
c) Mẫu số chung: 12
$\frac{{11}}{4} = \frac{{11 \times 3}}{{4 \times 3}} = \frac{{33}}{{12}}$
Quy đồng mẫu số hai phân số $\frac{{17}}{{12}}$ và $\frac{{11}}{4}$ ta được $\frac{{17}}{{12}}$ và $\frac{{33}}{{12}}$
Quy đồng mẫu số các phân số sau (theo mẫu):

Phương pháp giải:
Khi quy đồng mẫu số của hai phân số mà mẫu số lớn chia hết cho mẫu số bé, ta làm như sau:
- Lấy mẫu số lớn hơn là mẫu số chung
- Lấy mẫu số chung chia cho mẫu số bé
- Nhân cả tử số và mẫu số của phân số có mẫu số bé với thương vừa tìm được
Lời giải chi tiết:
a) $\frac{7}{{24}}$ ; $\frac{7}{6}$ ; $\frac{{11}}{8}$
Ta thấy 24 chia hết cho cả 6 và 8. Vậy mẫu số chung là 24
Ta có: 24 : 6 = 4 ; 24 : 8 = 3
$\frac{7}{6} = \frac{{7 \times 4}}{{6 \times 4}} = \frac{{28}}{{24}}$ ; $\frac{{11}}{8} = \frac{{11 \times 3}}{{8 \times 3}} = \frac{{33}}{{24}}$ ; giữ nguyên $\frac{7}{{24}}$
Quy đồng mẫu số ba phân số $\frac{7}{{24}}$ ; $\frac{7}{6}$ ; $\frac{{11}}{8}$ ta được $\frac{7}{{24}}$ ; $\frac{{28}}{{24}}$ ; $\frac{{33}}{{24}}$
b) $\frac{2}{7}$ ; $\frac{7}{{35}}$ ; $\frac{9}{5}$
Ta thấy 35 chia hết cho cả 7 và 5. Vậy mẫu số chung là 35
Ta có 35 : 7 = 5 ; 35 : 5 = 7
$\frac{2}{7} = \frac{{2 \times 5}}{{7 \times 5}} = \frac{{10}}{{35}}$ ; $\frac{9}{5} = \frac{{9 \times 7}}{{5 \times 7}} = \frac{{63}}{{35}}$ ; giữ nguyên $\frac{7}{{35}}$
Quy đồng mẫu số ba phân số $\frac{2}{7}$ ; $\frac{7}{{35}}$ ; $\frac{9}{5}$ ta được $\frac{{10}}{{35}}$ ; $\frac{7}{{35}}$ ; $\frac{{63}}{{35}}$
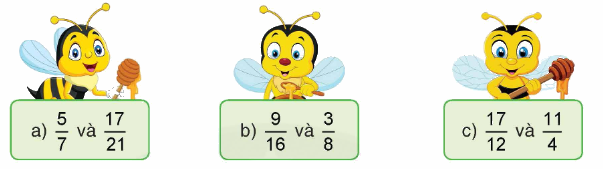
Quy đồng mẫu số các phân số sau:
Phương pháp giải:
Khi quy đồng mẫu số của hai phân số mà mẫu số lớn chia hết cho mẫu số bé, ta làm như sau:
- Lấy mẫu số lớn hơn là mẫu số chung
- Lấy mẫu số chung chia cho mẫu số bé
- Nhân cả tử số và mẫu số của phân số có mẫu số bé với thương vừa tìm được
Lời giải chi tiết:
a) Mẫu số chung là 21
$\frac{5}{7} = \frac{{5 \times 3}}{{7 \times 3}} = \frac{{15}}{{21}}$, giữ nguyên $\frac{{17}}{{21}}$
Quy đồng mẫu số hai phân số $\frac{5}{7}$ và $\frac{{17}}{{21}}$ ta được $\frac{{15}}{{21}}$ và $\frac{{17}}{{21}}$
b) Mẫu số chung là 16
$\frac{3}{8} = \frac{{3 \times 2}}{{8 \times 2}} = \frac{6}{{16}}$
Quy đồng mẫu số hai phân số $\frac{9}{{16}}$ và $\frac{3}{8}$ ta được $\frac{9}{{16}}$ và $\frac{6}{{16}}$
c) Mẫu số chung: 12
$\frac{{11}}{4} = \frac{{11 \times 3}}{{4 \times 3}} = \frac{{33}}{{12}}$
Quy đồng mẫu số hai phân số $\frac{{17}}{{12}}$ và $\frac{{11}}{4}$ ta được $\frac{{17}}{{12}}$ và $\frac{{33}}{{12}}$
Quy đồng mẫu số các phân số sau (theo mẫu):

Phương pháp giải:
Khi quy đồng mẫu số của hai phân số mà mẫu số lớn chia hết cho mẫu số bé, ta làm như sau:
- Lấy mẫu số lớn hơn là mẫu số chung
- Lấy mẫu số chung chia cho mẫu số bé
- Nhân cả tử số và mẫu số của phân số có mẫu số bé với thương vừa tìm được
Lời giải chi tiết:
a) $\frac{7}{{24}}$ ; $\frac{7}{6}$ ; $\frac{{11}}{8}$
Ta thấy 24 chia hết cho cả 6 và 8. Vậy mẫu số chung là 24
Ta có: 24 : 6 = 4 ; 24 : 8 = 3
$\frac{7}{6} = \frac{{7 \times 4}}{{6 \times 4}} = \frac{{28}}{{24}}$ ; $\frac{{11}}{8} = \frac{{11 \times 3}}{{8 \times 3}} = \frac{{33}}{{24}}$ ; giữ nguyên $\frac{7}{{24}}$
Quy đồng mẫu số ba phân số $\frac{7}{{24}}$ ; $\frac{7}{6}$ ; $\frac{{11}}{8}$ ta được $\frac{7}{{24}}$ ; $\frac{{28}}{{24}}$ ; $\frac{{33}}{{24}}$
b) $\frac{2}{7}$ ; $\frac{7}{{35}}$ ; $\frac{9}{5}$
Ta thấy 35 chia hết cho cả 7 và 5. Vậy mẫu số chung là 35
Ta có 35 : 7 = 5 ; 35 : 5 = 7
$\frac{2}{7} = \frac{{2 \times 5}}{{7 \times 5}} = \frac{{10}}{{35}}$ ; $\frac{9}{5} = \frac{{9 \times 7}}{{5 \times 7}} = \frac{{63}}{{35}}$ ; giữ nguyên $\frac{7}{{35}}$
Quy đồng mẫu số ba phân số $\frac{2}{7}$ ; $\frac{7}{{35}}$ ; $\frac{9}{5}$ ta được $\frac{{10}}{{35}}$ ; $\frac{7}{{35}}$ ; $\frac{{63}}{{35}}$
a) Viết 3 và $\frac{2}{3}$ thành hai phân số đều có mẫu số là 3
b) Viết $\frac{2}{3}$ ; 5 và $\frac{7}{{12}}$ thành ba phân số đều có mẫu số bằng 12.
Phương pháp giải:
- Lấy mẫu số chung chia cho mẫu số của phân số cần quy đồng
- Nhân cả tử số và mẫu số của phân số với thương vừa tìm được
Lời giải chi tiết:
a) $3 = \frac{9}{3}$ ; giữ nguyên $\frac{2}{3}$
b) $\frac{2}{3} = \frac{8}{{12}}$ ; $5 = \frac{{60}}{{12}}$ ; giữ nguyên $\frac{7}{{12}}$
Số?
Ba đội vận tải được giao vận chuyển một lô hàng. Đội Một vận chuyển được $\frac{1}{7}$ lô hàng, đội Hai vận chuyển được $\frac{4}{{21}}$ lô hàng và đội Ba vận chuyển được $\frac{2}{3}$ lô hàng. Vậy:
a) Đội Một vận chuyển được $\frac{?}{{21}}$ lô hàng.
b) Đội Ba vận chuyển được $\frac{?}{{21}}$ lô hàng.
Phương pháp giải:
a) Quy đồng phân số $\frac{1}{7}$ với mẫu số chung là 21
b) Quy đồng phân số $\frac{2}{3}$ với mẫu số chung là 21
Lời giải chi tiết:
a) Ta có $\frac{1}{7} = \frac{3}{{21}}$. Đội Một vận chuyển được $\frac{3}{{21}}$ lô hàng.
b) Ta có $\frac{2}{3} = \frac{{14}}{{21}}$. Đội Ba vận chuyển được $\frac{{14}}{{21}}$ lô hàng.
Bài 100 trang 18 Toán lớp 4 thuộc chương trình Toán 4, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến cộng, trừ, nhân, chia các số tự nhiên, các bài toán có dạng tổng, hiệu, tích, thương. Việc nắm vững kiến thức và kỹ năng này là nền tảng quan trọng cho các bài học tiếp theo.
Bài tập luyện tập trang 18 bao gồm nhiều dạng bài khác nhau, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các tình huống cụ thể. Các dạng bài chính bao gồm:
Bài tập này yêu cầu học sinh tính nhẩm nhanh các phép tính đơn giản. Ví dụ:
a) 25 + 15 = ?
b) 40 - 20 = ?
c) 5 x 6 = ?
d) 30 : 5 = ?
Để tính nhẩm nhanh, học sinh có thể sử dụng các kỹ năng cộng, trừ, nhân, chia đã học, hoặc sử dụng các mẹo nhỏ như phân tích số, nhóm số để tính toán dễ dàng hơn.
Bài tập này yêu cầu học sinh đọc kỹ đề bài, xác định được các yếu tố quan trọng như số liệu, đơn vị đo, câu hỏi, và sau đó vận dụng các phép tính phù hợp để giải quyết bài toán. Ví dụ:
Một cửa hàng có 35 kg gạo tẻ và 20 kg gạo nếp. Hỏi cửa hàng có tất cả bao nhiêu ki-lô-gam gạo?
Bài giải:
Số ki-lô-gam gạo cửa hàng có tất cả là:
35 + 20 = 55 (kg)
Đáp số: 55 kg
Khi giải bài toán có lời văn, học sinh cần chú ý đến đơn vị đo và đảm bảo rằng đáp số có đơn vị đo phù hợp.
Bài tập này yêu cầu học sinh tìm giá trị của x trong các biểu thức toán học. Ví dụ:
x + 15 = 30
Để tìm x, học sinh cần thực hiện các phép toán ngược lại với các phép toán trong biểu thức. Trong trường hợp này, ta thực hiện phép trừ:
x = 30 - 15
x = 15
Các bài tập tổng hợp thường yêu cầu học sinh vận dụng nhiều kiến thức và kỹ năng khác nhau để giải quyết. Ví dụ, một bài toán có thể yêu cầu học sinh tính tổng, hiệu, tích, thương của các số, sau đó so sánh kết quả, hoặc giải một bài toán có lời văn phức tạp.
Hy vọng với những hướng dẫn chi tiết và lời giải bài tập trên, các em học sinh lớp 4 sẽ tự tin hơn trong việc học tập và giải quyết các bài toán Toán lớp 4 trang 18 - Bài 100: Luyện tập - SGK Bình Minh. Chúc các em học tốt!