Bài 143 Toán lớp 4 trang 70 thuộc chương trình Luyện tập chung trong sách giáo khoa Toán 4 Bình Minh. Bài học này giúp các em học sinh củng cố kiến thức đã học về các phép tính với số có nhiều chữ số, giải toán có lời văn và các bài toán liên quan đến hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong bài học này, giúp các em học sinh tự tin hơn trong việc giải toán và đạt kết quả tốt nhất.
Tính bằng cách thuận tiện.
Đội vận tải được giao vận chuyển 690 tấn hàng. Trong ngày đầu, độ đã vận chuyển được $\frac{2}{5}$ số tấn hàng được giao. Hỏi sau ngày đầu, đội vận tải còn lại bao nhiêu tấn hàng cần vận chuyển?
Phương pháp giải:
- Tìm số tấn hàng đã vận chuyển trong ngày đầu = Số tấn hàng được giao vận chuyển x $\frac{2}{5}$
- Số tấn hàng còn lại = Số tấn hàng được giao vận chuyển – số tấn hàng đã vận chuyển
Lời giải chi tiết:
Số tấn hàng đã vận chuyển trong ngày đầu là:
$690 \times \frac{2}{5} = 276$ (tấn)
Sau ngày đầu, đội vận tải còn lại số tấn hàng cần vận chuyển là:
690 – 276 = 414 (tấn)
Đáp số: 414 tấn hàng
Tính giá trị của biểu thức:

Phương pháp giải:
- Muốn cộng hoặc trừ các phân số khác mẫu số, ta quy đồng mẫu số các phân số rồi cộng hoặc trừ các phân số sau khi quy đồng.
- Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số
Lời giải chi tiết:
a) $\frac{5}{6} + \frac{7}{{18}} + \frac{1}{9} = \frac{{15}}{{18}} + \frac{7}{{18}} + \frac{2}{{18}} = \frac{{24}}{{18}} = \frac{4}{3}$
b) $\frac{5}{7} - \frac{8}{{21}} = \frac{{15}}{{21}} - \frac{8}{{21}} = \frac{7}{{21}} = \frac{1}{3}$
c) $\frac{9}{{14}} \times 7 \times \frac{{11}}{6} = \frac{9}{2} \times \frac{{11}}{6} = \frac{{99}}{{12}} = \frac{{33}}{4}$
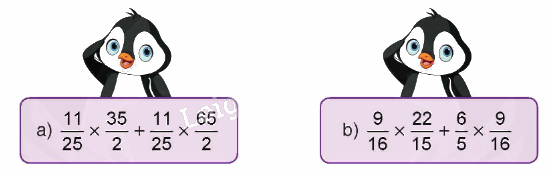
Tính bằng cách thuận tiện.
Phương pháp giải:
Áp dụng công thức: a x b + a x c = a x (b + c)
Lời giải chi tiết:
a) $\frac{{11}}{{25}} \times \frac{{35}}{2} + \frac{{11}}{{25}} \times \frac{{65}}{2} = \frac{{11}}{{25}} \times \left( {\frac{{35}}{2} + \frac{{65}}{2}} \right) = \frac{{11}}{{25}} \times 50 = 22$
b) $\frac{9}{{16}} \times \frac{{22}}{{15}} + \frac{6}{5} \times \frac{9}{{16}} = \frac{9}{{16}} \times \left( {\frac{{22}}{{15}} + \frac{6}{5}} \right) = \frac{9}{{16}} \times \left( {\frac{{22}}{{15}} + \frac{{18}}{{15}}} \right) = \frac{9}{{16}} \times \frac{8}{3} = \frac{{72}}{{48}} = \frac{3}{2}$

Tìm phân số đảo ngược của các phân số sau:

Phương pháp giải:
Quan sát ví dụ mẫu rồi tìm phân số đảo ngược của phân số đã cho.
Lời giải chi tiết:
a) $\frac{4}{3}$ là phân số đảo ngược của $\frac{3}{4}$
b) $\frac{6}{{19}}$ là phân số đảo ngược của $\frac{{19}}{6}$
c) $\frac{5}{1}$ là phân số đảo ngược của $\frac{1}{5}$
d) $\frac{1}{8}$ là phân số đảo ngược của $\frac{8}{1}$
Tính giá trị của biểu thức:

Phương pháp giải:
- Muốn cộng hoặc trừ các phân số khác mẫu số, ta quy đồng mẫu số các phân số rồi cộng hoặc trừ các phân số sau khi quy đồng.
- Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số
Lời giải chi tiết:
a) $\frac{5}{6} + \frac{7}{{18}} + \frac{1}{9} = \frac{{15}}{{18}} + \frac{7}{{18}} + \frac{2}{{18}} = \frac{{24}}{{18}} = \frac{4}{3}$
b) $\frac{5}{7} - \frac{8}{{21}} = \frac{{15}}{{21}} - \frac{8}{{21}} = \frac{7}{{21}} = \frac{1}{3}$
c) $\frac{9}{{14}} \times 7 \times \frac{{11}}{6} = \frac{9}{2} \times \frac{{11}}{6} = \frac{{99}}{{12}} = \frac{{33}}{4}$
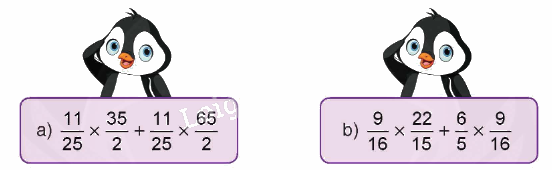
Tính bằng cách thuận tiện.
Phương pháp giải:
Áp dụng công thức: a x b + a x c = a x (b + c)
Lời giải chi tiết:
a) $\frac{{11}}{{25}} \times \frac{{35}}{2} + \frac{{11}}{{25}} \times \frac{{65}}{2} = \frac{{11}}{{25}} \times \left( {\frac{{35}}{2} + \frac{{65}}{2}} \right) = \frac{{11}}{{25}} \times 50 = 22$
b) $\frac{9}{{16}} \times \frac{{22}}{{15}} + \frac{6}{5} \times \frac{9}{{16}} = \frac{9}{{16}} \times \left( {\frac{{22}}{{15}} + \frac{6}{5}} \right) = \frac{9}{{16}} \times \left( {\frac{{22}}{{15}} + \frac{{18}}{{15}}} \right) = \frac{9}{{16}} \times \frac{8}{3} = \frac{{72}}{{48}} = \frac{3}{2}$

Tìm phân số đảo ngược của các phân số sau:

Phương pháp giải:
Quan sát ví dụ mẫu rồi tìm phân số đảo ngược của phân số đã cho.
Lời giải chi tiết:
a) $\frac{4}{3}$ là phân số đảo ngược của $\frac{3}{4}$
b) $\frac{6}{{19}}$ là phân số đảo ngược của $\frac{{19}}{6}$
c) $\frac{5}{1}$ là phân số đảo ngược của $\frac{1}{5}$
d) $\frac{1}{8}$ là phân số đảo ngược của $\frac{8}{1}$
Đội vận tải được giao vận chuyển 690 tấn hàng. Trong ngày đầu, độ đã vận chuyển được $\frac{2}{5}$ số tấn hàng được giao. Hỏi sau ngày đầu, đội vận tải còn lại bao nhiêu tấn hàng cần vận chuyển?
Phương pháp giải:
- Tìm số tấn hàng đã vận chuyển trong ngày đầu = Số tấn hàng được giao vận chuyển x $\frac{2}{5}$
- Số tấn hàng còn lại = Số tấn hàng được giao vận chuyển – số tấn hàng đã vận chuyển
Lời giải chi tiết:
Số tấn hàng đã vận chuyển trong ngày đầu là:
$690 \times \frac{2}{5} = 276$ (tấn)
Sau ngày đầu, đội vận tải còn lại số tấn hàng cần vận chuyển là:
690 – 276 = 414 (tấn)
Đáp số: 414 tấn hàng
Bài 143 Toán lớp 4 trang 70 là một bài luyện tập quan trọng, giúp học sinh ôn lại và vận dụng các kiến thức đã học trong chương trình Toán 4. Bài tập bao gồm nhiều dạng khác nhau, đòi hỏi học sinh phải nắm vững các phép tính cơ bản, khả năng phân tích đề bài và lựa chọn phương pháp giải phù hợp.
Bài 143 Luyện tập chung Toán lớp 4 trang 70 bao gồm các bài tập sau:
Để tính nhẩm nhanh, học sinh cần nắm vững bảng cửu chương, các quy tắc cộng, trừ, nhân, chia và thực hành thường xuyên. Ví dụ:
25 + 15 = ?
40 - 10 = ?
5 x 6 = ?
30 : 5 = ?
Khi giải bài toán có lời văn, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lập kế hoạch giải bài toán và thực hiện các phép tính cần thiết. Ví dụ:
Một cửa hàng có 35 kg gạo. Buổi sáng bán được 12 kg gạo, buổi chiều bán được 15 kg gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Bài giải:
Số gạo đã bán là: 12 + 15 = 27 (kg)
Số gạo còn lại là: 35 - 27 = 8 (kg)
Đáp số: 8 kg
Khi tính giá trị biểu thức, học sinh cần thực hiện các phép tính theo đúng thứ tự: trong ngoặc trước, ngoài ngoặc sau, nhân chia trước, cộng trừ sau. Ví dụ:
(10 + 5) x 2 = ?
20 : 4 + 3 = ?
Để giải các bài toán hình học, học sinh cần nắm vững các công thức tính chu vi, diện tích của các hình chữ nhật, hình vuông. Ví dụ:
Một hình chữ nhật có chiều dài 10 cm, chiều rộng 5 cm. Tính chu vi và diện tích của hình chữ nhật đó.
Bài giải:
Chu vi của hình chữ nhật là: (10 + 5) x 2 = 30 (cm)
Diện tích của hình chữ nhật là: 10 x 5 = 50 (cm2)
Đáp số: Chu vi: 30 cm, Diện tích: 50 cm2
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán lớp 4 trang 70 - Bài 143: Luyện tập chung - SGK Bình Minh. Chúc các em học tốt!