Bài viết này sẽ hướng dẫn chi tiết cách áp dụng các trường hợp đồng dạng của tam giác để giải quyết các bài toán liên quan đến tam giác vuông. Chúng ta sẽ cùng nhau khám phá các kiến thức nền tảng, các ví dụ minh họa và các bài tập thực hành để bạn có thể tự tin vận dụng kiến thức vào giải toán.
Hiểu rõ về đồng dạng tam giác và cách áp dụng vào tam giác vuông là một kỹ năng quan trọng trong chương trình học toán học cấp trung học cơ sở và trung học phổ thông.
Có thể áp dụng các trường hợp đồng dạng nào của tam giác vào tam giác vuông? Trường hợp hai cạnh góc vuông là gì? Trường hợp góc – góc trong tam giác vuông là gì?
1. Lý thuyết
- Trường hợp hai cạnh góc vuông:
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

- Trường hợp góc – góc:
Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
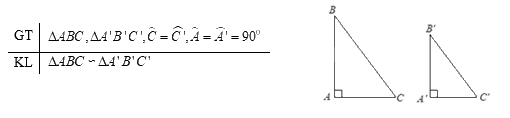
2. Ví dụ minh họa
Ví dụ 1: Cho tam giác ${ABC}$ vuông tại ${A}$ có ${AB = 1}$ cm, ${AC = 3}$ cm. Trên cạnh ${AC}$ lấy ${D}$, ${E}$ sao cho ${AD = DE = EC}$. Chứng minh
a) $\Delta DBE\backsim \Delta DCB$; b) $\widehat{AEB}+\widehat{ACB}={{45}^{0}}$.
Lời giải.
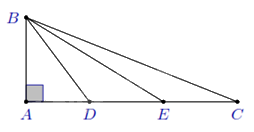
a) Tính được ${DB^2 = 2}$, từ đó ta có
$D{{B}^{2}}=DE\cdot DC\Rightarrow \frac{DB}{DE}=\frac{DC}{DB}\Rightarrow \Delta DBE\backsim \Delta DCB$ (c.g.c).
b) Từ câu a), ta có
$\widehat{AEB}=\widehat{DBC}\text{ }\Rightarrow \widehat{AEB}+\widehat{ACB}=\widehat{DBC}+\widehat{ACB}=\widehat{ADB}={{45}^{0}}$.
Ví dụ 2: Cho tam giác ${ABC}$ vuông tại ${A}$, đường cao ${AH}$. Tia phân giác của ${\widehat{B}}$ cắt ${AH}$, ${AC}$ lần lượt tại ${D}$, ${E}$.
a) Chứng minh $\Delta BAD\backsim \Delta BCE$ và \(\Delta BHD\backsim \Delta BAE\).
b) Chứng minh ${\frac{DH}{DA}=\frac{EA}{EC}}$.
Lời giải
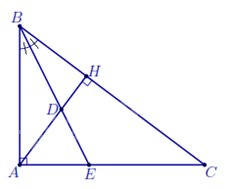
a) Xét $\Delta BAD$ và $\Delta BCE$ có ${\widehat{ABD}=\widehat{EBC}}$ và ${\widehat{BAD}=\widehat{ECB}}$ (góc có cặp cạnh tương ứng vuông góc) $\Rightarrow \Delta BAD\backsim \Delta BCE$ (g.g).
Xét $\Delta BHD$ và $\Delta BAE$ có $\widehat{BHD}=\widehat{BAE}={{90}^{0}}$
và $\widehat{HBD}=\widehat{ABE}\Rightarrow \Delta BAD\backsim \Delta BCE$ (g.g).
b) Từ kết quả câu a), ta có ${\frac{DH}{EA}=\frac{BD}{BE}=\frac{DA}{CE} \Rightarrow \frac{DH}{DA}=\frac{EA}{EC}}$.
Trong hình học, hai tam giác được gọi là đồng dạng nếu chúng có cùng hình dạng nhưng kích thước có thể khác nhau. Điều này có nghĩa là các góc tương ứng của hai tam giác bằng nhau và các cạnh tương ứng tỉ lệ với nhau. Việc hiểu rõ về đồng dạng tam giác là nền tảng quan trọng để giải quyết nhiều bài toán hình học, đặc biệt là các bài toán liên quan đến tam giác vuông.
Có ba trường hợp đồng dạng tam giác thường được sử dụng:
Tam giác vuông là một loại tam giác đặc biệt có một góc vuông (90 độ). Khi áp dụng các trường hợp đồng dạng vào tam giác vuông, chúng ta cần lưu ý một số điểm sau:
Ví dụ 1: Cho tam giác ABC vuông tại A và tam giác A'B'C' vuông tại A'. Biết góc B = góc B' = 60o. Chứng minh tam giác ABC đồng dạng tam giác A'B'C'.
Giải:
Ví dụ 2: Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Cho tam giác A'B'C' vuông tại A', có A'B' = 6cm. Chứng minh tam giác ABC đồng dạng tam giác A'B'C'.
Giải:
1. Cho tam giác ABC vuông tại A, có AB = 5cm, AC = 12cm. Tính độ dài cạnh BC.
2. Cho tam giác ABC vuông tại A, có góc B = 45o. Tính các góc còn lại của tam giác.
3. Cho tam giác ABC vuông tại A, có đường cao AH. Chứng minh tam giác ABH đồng dạng tam giác CBA.
Việc nắm vững các trường hợp đồng dạng của tam giác và cách áp dụng chúng vào tam giác vuông là rất quan trọng để giải quyết các bài toán hình học một cách hiệu quả. Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học toán.