Chuyên đề Hình đồng dạng là một trong những kiến thức quan trọng trong chương trình Toán học lớp 8 và lớp 9. Nắm vững kiến thức về hình đồng dạng giúp học sinh giải quyết các bài toán hình học một cách hiệu quả và chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập đa dạng và phương pháp giải bài tập hình đồng dạng một cách dễ hiểu, giúp bạn tự tin chinh phục môn Toán.
Hình đồng dạng phối cảnh là gì? Hình đồng dạng là gì?
1. Lý thuyết
- Hình đồng dạng phối cảnh (Hình vị tự).
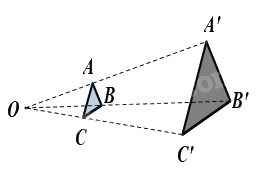
+ Hình ảnh bên từ điểm O, phóng to hai lần tam giác ABC, ta sẽ nhận được tam giác A’B’C’. Hai tam giác A’B’C’ và ABC gọi là đồng dạng phối cảnh (hay vị tự) với nhau, điểm O gọi là tâm đồng dạng phối cảnh, tỉ số \(k = \frac{{A'B'}}{{AB}} = 3\) gọi là tỉ số vị tự.
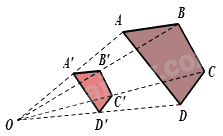
+ Hình ảnh bên từ điểm O, thu nhỏ hai lần tứ giác ABCD, ta sẽ nhận được tứ giác A’B’C’D’. Hai tứ giác A’B’C’D’ và ABCD gọi là đồng dạng phối cảnh (hay vị tự) với nhau, điểm O gọi là tâm đồng dạng phối cảnh, tỉ số \(k = \frac{{A'B'}}{{AB}} = \frac{1}{2}\) gọi là tỉ số vị tự.
+ Như vậy, bằng cách phóng to (nếu tỉ số vị tự k > 1) hay thu nhỏ (nếu tỉ số vị tự k < 1) hình H, ta sẽ nhận được hình H ’ đồng dạng phối cảnh (hay vị tự) với hình H.
+ Ta cũng gọi H ’ là hình đồng dạng phối cảnh (hay hình vị tự ) tỉ số k của hình H.
+ Hình đồng dạng phối cảnh tỉ số k của đoạn thẳng AB là một đoạn thẳng A’B’ ( nằm trên đường thẳng song song hoặc trùng với đường thẳng AB) và A’B’ = k.AB.
- Hình đồng dạng.
+ Nếu có thể đặt hình H chồng khít lên hình H ’ thì ta nói hai hình H và H ’ là bằng nhau (hay còn gọi là hình H bằng hình H ’).
+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.
2. Ví dụ minh họa
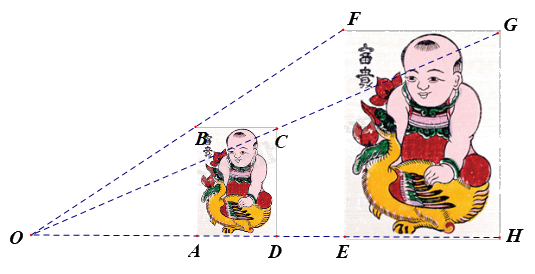
Hình chữ nhật ABCD và EFGH đồng dạng phối cảnh với điểm O gọi là tâm đồng dạng phối cảnh.
Ví dụ về hình đồng dạng:
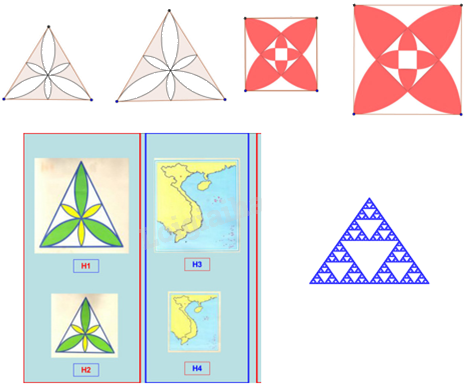
Hình đồng dạng là một khái niệm quan trọng trong hình học, đặc biệt là trong chương trình Toán lớp 8 và lớp 9. Hiểu rõ về hình đồng dạng không chỉ giúp học sinh giải quyết các bài toán một cách chính xác mà còn phát triển tư duy logic và khả năng suy luận không gian.
Hai hình được gọi là đồng dạng với nhau nếu chúng có cùng hình dạng nhưng kích thước có thể khác nhau. Điều này có nghĩa là một hình có thể được thu nhỏ hoặc phóng to để trở thành hình kia mà không làm thay đổi hình dạng ban đầu.
Tỉ số đồng dạng là tỉ số giữa hai kích thước tương ứng của hai hình đồng dạng. Ví dụ, nếu hai tam giác ABC và A'B'C' đồng dạng, thì tỉ số đồng dạng k được tính bằng:
k = A'B' / AB = B'C' / BC = C'A' / CA
Có ba trường hợp đồng dạng của tam giác thường được sử dụng:
Định lý Talet là một công cụ quan trọng để chứng minh sự đồng dạng của các tam giác. Định lý này phát biểu rằng nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó chia hai cạnh đó thành những đoạn thẳng tỉ lệ.
Định lý Thales là một trường hợp đặc biệt của định lý Talet, áp dụng cho các đường thẳng song song cắt các cạnh của một tam giác.
Hình đồng dạng có rất nhiều ứng dụng trong thực tế, bao gồm:
Dưới đây là một số bài tập vận dụng để giúp bạn hiểu rõ hơn về hình đồng dạng:
Hy vọng với những kiến thức và bài tập trên, bạn sẽ tự tin hơn khi học và giải quyết các bài toán liên quan đến hình đồng dạng. Chúc bạn học tốt!