Trong chương trình học toán lớp 8 và lớp 9, kiến thức về tam giác đồng dạng đóng vai trò vô cùng quan trọng. Trường hợp đồng dạng thứ nhất (c.c.c) là một trong những trường hợp cơ bản nhất để nhận biết hai tam giác đồng dạng. Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ và chi tiết về trường hợp đồng dạng này.
Chúng ta sẽ cùng tìm hiểu định nghĩa, điều kiện, và cách áp dụng trường hợp đồng dạng thứ nhất vào giải các bài toán thực tế.
Trường hợp đồng dạng thứ nhất là gì?
1. Lý thuyết
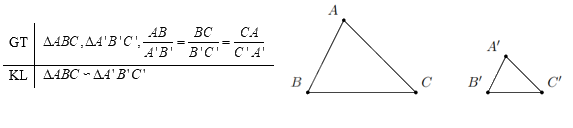
Định lí Trường hợp đồng dạng thứ nhất (cạnh – cạnh – cạnh):
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
2. Ví dụ minh họa
Hai tam giác mà các cạnh có độ dài ${6}$cm, ${9}$cm, ${12}$cm và ${24}$cm, ${18}$cm, ${12}$cm đồng dạng vì ${\frac{6}{12} = \frac{9}{18} = \frac{12}{24} = \frac{1}{2}}$.
Hai tam giác mà các cạnh có độ dài ${4}$cm, ${5}$cm, ${6}$cm và ${12}$cm, ${15}$cm, ${18}$cm đồng dạng vì ${\frac{4}{12} = \frac{5}{15} = \frac{6}{18} = \frac{1}{3}}$.
Trường hợp đồng dạng thứ nhất (c.c.c) của tam giác phát biểu như sau:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Kí hiệu: ΔABC ∽ ΔA'B'C' khi và chỉ khi:
Giải thích:
Tỉ lệ thức trên thể hiện rằng tỉ lệ giữa các cạnh tương ứng của hai tam giác là bằng nhau. Điều này có nghĩa là hai tam giác có hình dạng giống nhau, chỉ khác về kích thước.
Chứng minh trường hợp đồng dạng thứ nhất (c.c.c) có thể được thực hiện bằng cách sử dụng phép biến hình. Giả sử ta có hai tam giác ΔABC và ΔA'B'C' thỏa mãn AB/A'B' = BC/B'C' = CA/C'A' = k (k là một số dương).
Khi đó, ta có thể chứng minh được ΔABC ∽ ΔA'B'C'.
Ví dụ 1: Cho ΔABC có AB = 3cm, BC = 4cm, CA = 5cm và ΔA'B'C' có A'B' = 6cm, B'C' = 8cm, C'A' = 10cm. Chứng minh ΔABC ∽ ΔA'B'C'.
Giải:
Ta có:
Do đó, AB/A'B' = BC/B'C' = CA/C'A' = 1/2. Theo trường hợp đồng dạng thứ nhất (c.c.c), ta có ΔABC ∽ ΔA'B'C'.
Trường hợp đồng dạng thứ nhất được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác đồng dạng, đặc biệt là:
Bài 1: Cho ΔABC có AB = 2cm, BC = 3cm, CA = 4cm. ΔA'B'C' đồng dạng với ΔABC có cạnh lớn nhất là 8cm. Tính các cạnh còn lại của ΔA'B'C'.
Bài 2: Cho hình vẽ, biết AB = 6cm, AC = 9cm, DE = 4cm. Tính độ dài AD và EC.
(Hình vẽ minh họa cần được thêm vào đây)
Khi áp dụng trường hợp đồng dạng thứ nhất, cần đảm bảo rằng các cạnh được so sánh là các cạnh tương ứng của hai tam giác. Ngoài ra, cần chú ý đến thứ tự của các đỉnh khi viết tỉ lệ thức.
Trường hợp đồng dạng thứ nhất (c.c.c) là một công cụ quan trọng trong việc giải các bài toán liên quan đến tam giác đồng dạng. Việc nắm vững định nghĩa, điều kiện, và cách áp dụng trường hợp này sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và chính xác.