Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng các bài tập thực hành giúp bạn nắm vững kiến thức này.
Hãy cùng khám phá những tính chất đặc biệt của hình chữ nhật và ứng dụng của chúng trong giải toán!
Hình chữ nhật có tính chất gì?
1. Lý thuyết
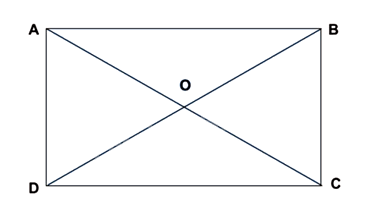
- Tính chất hình chữ nhật: Trong hình chữ nhật,
+ Hai cạnh đối song song và bằng nhau
+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
+ Hình chữ nhật có tất cả tính chất của hình thang và hình bình hành.
- Tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông.
+ Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
+ Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
2. Ví dụ minh họa
Ví dụ 1.
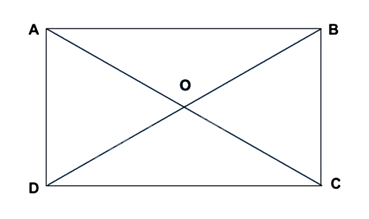
ABCD là hình chữ nhật
\( \Leftrightarrow \) \(\left\{ \begin{array}{l}AB = CD\\AD = BC\\AC = BD\\O = AC \cap BD \Rightarrow AO = OC;BO = OD\end{array} \right.\)
Ví dụ 2.
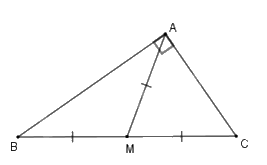
+ Nếu tam giác ABC vuông tại \(A\) và \(M\) là trung điểm cạnh BC thì \(AM = BM = CM = \frac{{BC}}{2}.\)
+ Nếu tam giác ABC có \(M\) là trung điểm BC và \(AM = \frac{{BC}}{2}\) thì \(\Delta ABC\) vuông tại A.
Hình chữ nhật là một trong những hình tứ giác đặc biệt, đóng vai trò quan trọng trong chương trình Hình học lớp 8. Việc nắm vững các tính chất của hình chữ nhật không chỉ giúp học sinh giải quyết các bài toán liên quan đến hình học mà còn là nền tảng cho việc học các kiến thức nâng cao hơn.
Hình chữ nhật là tứ giác có bốn góc vuông. Điều này có nghĩa là mỗi góc của hình chữ nhật đều bằng 90 độ.
Có một số dấu hiệu để nhận biết một tứ giác có phải là hình chữ nhật hay không:
Hình chữ nhật có những tính chất quan trọng sau:
Các tính chất của hình chữ nhật có thể được chứng minh dựa trên các định lý và tính chất của tam giác vuông. Ví dụ, để chứng minh hai đường chéo bằng nhau, ta có thể sử dụng định lý Pytago trong hai tam giác vuông tạo bởi các cạnh và đường chéo của hình chữ nhật.
Các tính chất của hình chữ nhật được ứng dụng rộng rãi trong giải toán, đặc biệt là trong các bài toán liên quan đến tính độ dài cạnh, góc, đường chéo, diện tích và chu vi của hình chữ nhật.
Áp dụng định lý Pytago trong tam giác vuông ABC, ta có:
AC2 = AB2 + BC2 = 62 + 82 = 36 + 64 = 100
Suy ra AC = √100 = 10cm.
Vì O là trung điểm của AC, nên AO = OC = AC/2 = 12/2 = 6cm.
Hình vuông là một trường hợp đặc biệt của hình chữ nhật, trong đó tất cả các cạnh đều bằng nhau. Do đó, hình vuông cũng có tất cả các tính chất của hình chữ nhật, đồng thời có thêm một số tính chất riêng.
Để củng cố kiến thức về tính chất của hình chữ nhật, bạn có thể thực hành giải các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về tính chất của hình chữ nhật. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng chúng vào giải toán một cách hiệu quả.