Trong chương trình học Toán lớp 7, khái niệm về đường trung bình của tam giác là một kiến thức quan trọng. Bài viết này trên giaitoan.edu.vn sẽ cung cấp cho bạn định nghĩa chính xác, tính chất và ứng dụng của đường trung bình trong tam giác.
Chúng ta sẽ cùng nhau khám phá cách xác định đường trung bình, mối liên hệ giữa đường trung bình và cạnh đối diện, và cách sử dụng kiến thức này để giải các bài toán hình học một cách hiệu quả.
Đường trung bình của tam giác là gì?
1. Lý thuyết
Khái niệm: Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.
Chú ý:
+ Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+ Mỗi tam giác có ba đường trung bình.
2. Ví dụ minh họa
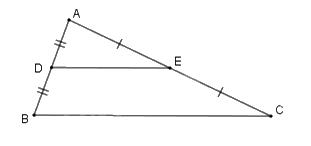
+ Tam giác ABC có D là trung điểm của AB, E là trung điểm của AC nên DE là đường trung bình của tam giác ABC.
+ Nếu $\left\{ \begin{array}{l}DA = DB\\DE{\rm{//}}BC\end{array} \right. \Rightarrow EC = EA$ .
Đường trung bình của tam giác là đoạn thẳng nối trung điểm của hai cạnh của tam giác. Để hiểu rõ hơn về khái niệm này, chúng ta cần nắm vững định nghĩa và các tính chất liên quan.
Trong tam giác ABC, nếu M là trung điểm của cạnh AB và N là trung điểm của cạnh AC, thì đoạn thẳng MN được gọi là đường trung bình của tam giác ABC, ứng với cạnh BC.
Trung điểm của một đoạn thẳng là điểm nằm chính giữa đoạn thẳng đó. Để xác định trung điểm M của đoạn thẳng AB, ta sử dụng công thức:
M = (xA + xB) / 2, (yA + yB) / 2
Trong đó, A(xA, yA) và B(xB, yB) là tọa độ của hai điểm đầu mút của đoạn thẳng AB.
Đường trung bình của tam giác có những tính chất quan trọng sau:
Chứng minh đường trung bình song song với cạnh đối diện:
Xét tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Ta có AM = MB và AN = NC. Xét tam giác AMN và tam giác ABC, ta thấy góc MAN chung và AM/AB = AN/AC = 1/2. Do đó, tam giác AMN đồng dạng với tam giác ABC theo trường hợp cạnh-góc-cạnh. Suy ra MN song song với BC.
Chứng minh độ dài đường trung bình bằng một nửa độ dài cạnh đối diện:
Vì tam giác AMN đồng dạng với tam giác ABC (cmt) nên MN/BC = AM/AB = 1/2. Suy ra MN = 1/2 BC.
Đường trung bình của tam giác được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến tính độ dài đoạn thẳng, chứng minh tính song song, và chứng minh các tính chất của hình thang.
Bài toán: Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Biết BC = 10cm. Tính độ dài MN.
Giải:
Vì MN là đường trung bình của tam giác ABC ứng với cạnh BC nên MN = 1/2 BC = 1/2 * 10cm = 5cm.
Ngoài đường trung bình của tam giác, còn có khái niệm về đường trung tuyến của tam giác. Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Đường trung tuyến và đường trung bình là hai khái niệm khác nhau và có những tính chất riêng biệt.
Để nắm vững kiến thức về đường trung bình của tam giác, bạn nên luyện tập thường xuyên các bài tập khác nhau. Hãy tìm kiếm các bài tập trên giaitoan.edu.vn hoặc trong sách giáo khoa để rèn luyện kỹ năng giải toán.
Đường trung bình của tam giác là một khái niệm quan trọng trong hình học. Việc hiểu rõ định nghĩa, tính chất và ứng dụng của đường trung bình sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Hãy tiếp tục học tập và khám phá thêm nhiều kiến thức thú vị khác trên giaitoan.edu.vn!