Tứ giác lồi là một khái niệm quan trọng trong hình học, thường xuất hiện trong chương trình toán lớp 8 và lớp 9.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu về tứ giác lồi, giúp bạn nắm vững kiến thức nền tảng và áp dụng vào giải quyết các bài tập thực tế.
Hãy cùng khám phá thế giới của tứ giác lồi và nâng cao kỹ năng giải toán của bạn!
Tứ giác là gì? Tứ giác lồi là gì?
1. Lý thuyết
Khái niệm:
+ Tứ giác là hình gồm bốn đoạn thẳng, trong đó không có hai đoạn thẳng nào cùng nằm trên một đường thẳng.
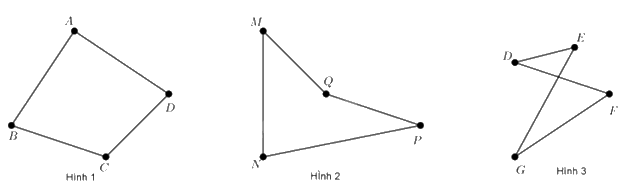
+ Tứ giác lồi là tứ giác mà hai đỉnh thuộc một cạnh bất kì luôn nằm về một phía của đường thẳng đi qua hai đỉnh còn lại.
2. Ví dụ minh họa
- Ví dụ: Trong các hình dưới đây, hình 1 được gọi là tứ giác lồi.
- Chú ý: Dạng bài toán thường gặp: Bài toán liên quan đến cạnh và đường chéo của tứ giác lồi
Phương pháp giải:
Ta có thể chia tứ giác thành các tam giác, sau đó vận dụng bất đẳng thức tam giác.
Ví dụ: Cho tam giác ABCD. Chứng minh \(AC + BD > \frac{p}{2}\) (p là chu vi tứ giác).
Lời giải:
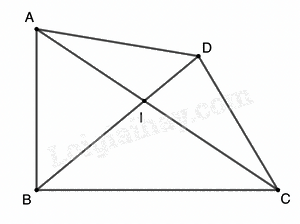
Gọi I là giao điểm của AC và BD. Theo bất đẳng thức tam giác ta có:
\(IA + IB > AB\);
\(IB + IC > BC\);
\(IC + ID > CD\);
\(ID + IA > AD\).
Cộng từng vế, ta được:
\(IA + IB + IB + IC + IC + ID + ID + IA > AB + BC + CD + DA\)
\(2(IA + IB + IC + ID) > AB + BC + CD + DA\)
\(2[(IA + IB) + (IC + ID)] > p\)
\(2(AC + BD) > p\)
\(AC + BD > \frac{p}{2}\) (đpcm)
Tứ giác lồi là một tứ giác mà tất cả các góc trong đều nhỏ hơn 180 độ. Nói cách khác, nếu nối một điểm bất kỳ bên trong tứ giác với bốn đỉnh của nó, các đoạn thẳng nối này đều nằm hoàn toàn bên trong tứ giác. Đây là một định nghĩa quan trọng để phân biệt tứ giác lồi với các loại tứ giác khác như tứ giác lõm.
Tứ giác lồi có nhiều tính chất quan trọng, giúp chúng ta giải quyết các bài toán liên quan. Một số tính chất cơ bản bao gồm:
Có nhiều dấu hiệu để nhận biết một tứ giác là tứ giác lồi. Một số dấu hiệu phổ biến bao gồm:
Ngoài các loại tứ giác lồi cơ bản như hình thang, hình thoi, hình chữ nhật và hình vuông, còn có một số loại tứ giác lồi đặc biệt khác, chẳng hạn như:
Tứ giác lồi xuất hiện rất nhiều trong thực tế, từ các công trình kiến trúc đến các vật dụng hàng ngày. Ví dụ:
Dưới đây là một số bài tập về tứ giác lồi và hướng dẫn giải:
Cho tứ giác ABCD có góc A = 80 độ, góc B = 100 độ, góc C = 120 độ. Tính góc D.
Hướng dẫn giải:
Áp dụng tính chất tổng bốn góc trong của một tứ giác lồi, ta có:
Góc D = 360 độ - (góc A + góc B + góc C) = 360 độ - (80 độ + 100 độ + 120 độ) = 60 độ.
Cho hình thang ABCD (AB // CD). Biết góc A = 60 độ, góc C = 120 độ. Tính góc B và góc D.
Hướng dẫn giải:
Vì AB // CD, nên góc A + góc D = 180 độ và góc B + góc C = 180 độ.
Suy ra: góc D = 180 độ - góc A = 180 độ - 60 độ = 120 độ.
góc B = 180 độ - góc C = 180 độ - 120 độ = 60 độ.
Một số công thức liên quan đến tứ giác lồi:
Để học tốt về tứ giác lồi, bạn nên:
Hy vọng với những kiến thức và bài tập trên, bạn sẽ hiểu rõ hơn về tứ giác lồi và tự tin giải quyết các bài toán liên quan. Chúc bạn học tốt!