Bài viết này sẽ cung cấp kiến thức toàn diện về thể tích của hình chóp tứ giác đều, một khái niệm quan trọng trong hình học không gian lớp 12. Chúng ta sẽ cùng nhau khám phá công thức tính thể tích, các ví dụ minh họa và bài tập thực hành để nắm vững kiến thức này.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp các bài giảng chất lượng cao và tài liệu học tập phong phú, giúp bạn học toán hiệu quả và đạt kết quả tốt nhất.
Công thức tính thể tích của hình chóp tứ giác đều là gì?
1. Lý thuyết
- Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với chiều cao
- Công thức tổng quát : \(V = \frac{1}{3}.S.h\) . Với :
+ V : Thể tích của hình chóp tứ giác đều.
+ S : Diện tích đáy.
+ h : Chiều cao của hình chóp tứ giác đều.
2. Ví dụ minh họa
Cho hình chóp tứ giác đều S.ABCD biết AD = 25mm, SO = 27mm. Tính thể tích hình chóp tứ giác đều S.ABCD ?
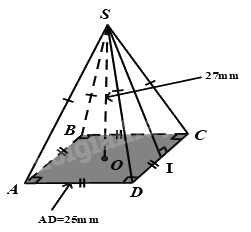
Lời giải
Thể tích hình chóp tứ giác đều S.ABCD là :
\(V = \frac{1}{3}.S.h = \frac{1}{3}{.25^2}.27 = 5625(m{m^3})\)
Hình chóp tứ giác đều là một hình đa diện có đáy là một tứ giác đều và các mặt bên là các tam giác cân bằng nhau. Để hiểu rõ về thể tích của hình chóp này, chúng ta cần nắm vững các khái niệm cơ bản về hình học không gian và công thức tính diện tích hình tứ giác đều.
Thể tích (V) của hình chóp tứ giác đều được tính theo công thức sau:
V = (1/3) * B * h
Trong đó:
Diện tích đáy của hình chóp tứ giác đều là diện tích của hình vuông. Nếu cạnh đáy là 'a', thì diện tích đáy được tính như sau:
B = a2
Chiều cao 'h' của hình chóp thường được cho trước trong bài toán. Tuy nhiên, trong một số trường hợp, bạn cần sử dụng định lý Pitago hoặc các công thức lượng giác để tính chiều cao dựa trên các thông tin khác của hình chóp.
Ví dụ 1: Một hình chóp tứ giác đều có cạnh đáy là 5cm và chiều cao là 8cm. Tính thể tích của hình chóp.
Giải:
Diện tích đáy: B = 52 = 25 cm2
Thể tích: V = (1/3) * 25 * 8 = 66.67 cm3
Ví dụ 2: Một hình chóp tứ giác đều có thể tích là 100 cm3 và chiều cao là 6cm. Tính cạnh đáy của hình chóp.
Giải:
100 = (1/3) * B * 6
B = (100 * 3) / 6 = 50 cm2
a = √50 ≈ 7.07 cm
Công thức tính thể tích V = (1/3) * B * h không chỉ áp dụng cho hình chóp tứ giác đều mà còn áp dụng cho tất cả các loại hình chóp, bao gồm cả hình chóp tam giác đều, hình chóp n-giác đều. Điều quan trọng là phải xác định đúng diện tích đáy (B) và chiều cao (h) của hình chóp.
Việc tính thể tích hình chóp tứ giác đều có nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về thể tích của hình chóp tứ giác đều. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài toán thực tế. Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục toán học!