Định Lí Pytagore và Ứng Dụng

Định lí Pytagore và ứng dụng

Định Lí Pytagore: Nền Tảng Của Hình Học

Định lí Pytagore là một trong những định lý quan trọng nhất trong hình học, được ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và đời sống. Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ về định lí Pytagore, từ công thức, chứng minh đến các ứng dụng thực tế.

Tại giaitoan.edu.vn, chúng tôi mang đến phương pháp học toán online hiệu quả, giúp bạn dễ dàng tiếp thu và vận dụng kiến thức vào giải bài tập.

Định lí Pythagore là gì? Định lí Pythagore đảo là gì? Ta có thể sử dụng định lí Pythagore để giải quyết các vấn đề nào?

1. Lý thuyết

- Định lí Pythagore:

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

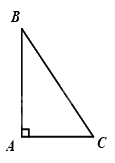
Định lí Pytagore và ứng dụng 1

\(\Delta ABC\) vuông tại \(A\) \( \Rightarrow B{C^2} = A{B^2} + A{C^2}\) .

- Định lí Pythagore đảo:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

\(\Delta ABC\) có\(\,B{C^2} = A{B^2} + A{C^2} \Rightarrow \widehat {BAC} = {90^0}\)

- Ứng dụng của định lí Pythagore

+ Tính độ dài đoạn thẳng

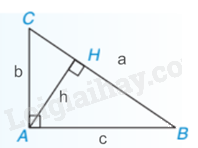
Nhận xét: Nếu tam giác vuông ABC tại A có đường cao AH = h, các cạnh BC = a, AC = b, AB = c thì h.a = b.c.

+ Chứng minh tính chất hình học

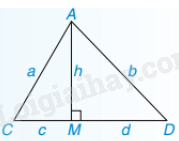
Chú ý: AM là đường cao, AC, AD là đường xiên thì đoạn thẳng MC là hình chiếu của đường xiên AC và MD là hình chiếu của đường xiên AD.

2. Ví dụ minh họa

Ví dụ 1: Cho tam giác \(ABC\) vuông tại \(A\), có \(AB = 6\)cm, \(AC = 8\)cm.

a) Tính độ dài cạnh \(BC\).

b) Kẻ \(AH\) vuông góc với \(BC\) tại \(H\). Biết \(AH = 4,8\) cm. Tính \(BH,CH\).

Lời giải

a) \(\Delta ABC\) vuông tại \(A\) nên theo định lí Pythagore ta có :

\(B{C^2} = A{B^2} + A{C^2} \Rightarrow B{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = \sqrt {100} = 10{\rm{ cm}}.\)

\(\Delta ABH\) vuông tại \(H\) nên theo định lí Pythagore ta có :

\(\begin{array}{l}A{B^2} = A{H^2} + B{H^2} \Rightarrow B{H^2} = A{B^2} - A{H^2}\\ \Rightarrow B{H^2} = {6^2} - {(4,8)^2} = 12,96 \Rightarrow BH = \sqrt {12,96} = 3,6{\rm{ cm}}.\end{array}\)

Từ đó tính được \(HC = BC - BH = 10 - 3,6 = 6,4\) cm.

Ví dụ 2: Cho tam giác \(ABC\) vuông tại \(A\), có \(AB = 6\) cm, \(AC = 8\) cm. \(D\) là một điểm sao cho \(BD = 16\) cm, \(CD = 24\) cm. Chứng minh \(\Delta CBD\) không thể là tam giác vuông.

Lời giải

Tam giác \(ABC\) vuông tại \(A\) nên theo định lý Pythagore ta có

\(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = \sqrt {100} = 10{\rm{ cm}}\)

Tam giác \(CBD\) không thể là tam giác vuông vì \({24^2} \ne {10^2} + {16^2}\).

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Định lí Pytagore và ứng dụng đặc sắc thuộc chuyên mục toán 8 sgk trên toán học. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Định Lí Pytagore: Khái Niệm Cơ Bản

Định lí Pytagore phát biểu rằng: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương của hai cạnh góc vuông. Công thức toán học biểu diễn định lí này là: a² + b² = c², trong đó 'c' là cạnh huyền (cạnh đối diện góc vuông) và 'a', 'b' là hai cạnh góc vuông.

Chứng Minh Định Lí Pytagore

Có rất nhiều cách chứng minh định lí Pytagore. Một trong những cách chứng minh phổ biến nhất là sử dụng diện tích hình vuông. Hãy tưởng tượng một hình vuông lớn có cạnh bằng (a + b). Bên trong hình vuông này, chúng ta có bốn tam giác vuông bằng nhau, mỗi tam giác có cạnh góc vuông là a và b, và cạnh huyền là c. Diện tích hình vuông lớn bằng (a + b)². Diện tích của bốn tam giác vuông là 4 * (1/2 * a * b) = 2ab. Diện tích phần còn lại của hình vuông lớn (phần không bị che bởi các tam giác) là c². Do đó, (a + b)² = 2ab + c². Khai triển (a + b)², ta được a² + 2ab + b² = 2ab + c². Rút gọn, ta có a² + b² = c².

Ứng Dụng Của Định Lí Pytagore

Định lí Pytagore có vô số ứng dụng trong thực tế và các lĩnh vực khác của toán học:

Tính độ dài cạnh của tam giác vuông: Nếu biết độ dài hai cạnh của một tam giác vuông, ta có thể sử dụng định lí Pytagore để tính độ dài cạnh còn lại.
Kiểm tra tam giác vuông: Nếu một tam giác có ba cạnh thỏa mãn a² + b² = c², thì tam giác đó là tam giác vuông.
Giải quyết các bài toán hình học: Định lí Pytagore được sử dụng để giải quyết nhiều bài toán liên quan đến hình học, chẳng hạn như tính chiều cao của một tam giác, tính khoảng cách giữa hai điểm.
Ứng dụng trong xây dựng và kiến trúc: Định lí Pytagore được sử dụng để đảm bảo tính vuông góc trong các công trình xây dựng, giúp đảm bảo sự ổn định và an toàn của công trình.
Ứng dụng trong hàng hải và hàng không: Định lí Pytagore được sử dụng để tính toán khoảng cách và hướng đi trong hàng hải và hàng không.

Bài Tập Vận Dụng Định Lí Pytagore

Dưới đây là một số bài tập vận dụng định lí Pytagore:

Một tam giác vuông có hai cạnh góc vuông lần lượt là 3cm và 4cm. Tính độ dài cạnh huyền.
Một chiếc thang dài 5m được dựa vào tường. Chân thang cách tường 3m. Tính chiều cao của bức tường.
Một mảnh đất hình chữ nhật có chiều dài 12m và chiều rộng 5m. Tính độ dài đường chéo của mảnh đất.

Định Lí Pytagore và Các Định Lí Liên Quan

Ngoài định lí Pytagore, còn có một số định lí liên quan đến tam giác vuông, chẳng hạn như:

Định lí cosin: c² = a² + b² - 2ab * cos(C), trong đó C là góc đối diện cạnh c.
Định lí sin: a/sin(A) = b/sin(B) = c/sin(C), trong đó A, B, C là các góc của tam giác.

Học Định Lí Pytagore Hiệu Quả Tại giaitoan.edu.vn

Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập phong phú và các tài liệu học tập hữu ích để giúp bạn nắm vững định lí Pytagore và các kiến thức toán học liên quan. Chúng tôi tin rằng với phương pháp học tập khoa học và sự hướng dẫn tận tình của đội ngũ giáo viên giàu kinh nghiệm, bạn sẽ đạt được kết quả tốt nhất trong học tập.

Bảng Tóm Tắt Công Thức Pytagore

Công Thức	Mô Tả
a² + b² = c²	Tính cạnh huyền khi biết hai cạnh góc vuông
a = √(c² - b²)	Tính cạnh góc vuông khi biết cạnh huyền và cạnh góc vuông còn lại
b = √(c² - a²)	Tính cạnh góc vuông khi biết cạnh huyền và cạnh góc vuông còn lại

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về định lí Pytagore và ứng dụng của nó. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.