Trong chương trình học Toán lớp 8, khái niệm về hai tam giác đồng dạng đóng vai trò then chốt. Việc nắm vững định nghĩa hai tam giác đồng dạng không chỉ giúp bạn giải quyết các bài toán liên quan đến hình học mà còn là bước đệm quan trọng cho các kiến thức nâng cao hơn.
Giaitoan.edu.vn xin giới thiệu bài viết chi tiết về định nghĩa hai tam giác đồng dạng, kèm theo các ví dụ minh họa và bài tập thực hành để bạn có thể hiểu rõ và áp dụng kiến thức một cách hiệu quả.
Khi nào thì hai tam giác đồng dạng? Tam giác đồng dạng có tính chất gì?
1. Lý thuyết
- Định nghĩa tam giác đồng dạng:
Hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.
Chú ý:
Khi tam giác ABC đồng dạng với tam giác A’B’C’.
+ Ta viết $\Delta ABC\,\backsim \,\Delta A'B'C'$ với các đỉnh được ghi theo thứ tự các góc tương ứng bằng nhau.
+ Tỉ số các cạnh tương ứng $\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CA}{C'A'}=k$ gọi là tỉ số đồng dạng.
- Tính chất của tam giác đồng dạng:
+ Mỗi tam giác đồng dạng với chính tam giác đó
+ Nếu $\Delta ABC\,\backsim \Delta A'B'C'$ thì $\Delta A'B'C'\backsim \,\Delta ABC$.
+ Nếu $\Delta A''B''C''\,\backsim \,\Delta A'B'C'$ và $\Delta A'B'C'\,\backsim \,\Delta ABC$ thì $\Delta A''B''C''\backsim \Delta ABC.$
2. Ví dụ minh họa
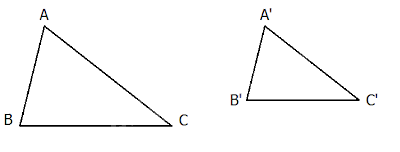
$\Delta ABC$ $\backsim $ $\Delta {A}'{B}'{C}'$ nếu $ \left\{ \begin{array}{*{35}{l}}\hat{A}=\hat{{A}'},\hat{B}=\hat{{B}'},\hat{C}=\hat{{C}'} \\ \frac{AB}{{A}'{B}'}=\frac{BC}{{B}'{C}'}=\frac{CA}{{C}'{A}'} \\ \end{array} \right.$
Hai tam giác được gọi là đồng dạng với nhau nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Có ba trường hợp đồng dạng tam giác thường gặp:
Ví dụ: Nếu AB/A'B' = BC/B'C' = CA/C'A' thì ΔABC ~ ΔA'B'C'.
Ví dụ: Nếu AB/A'B' = ∠B = ∠B' và ∠A = ∠A' thì ΔABC ~ ΔA'B'C'.
Ví dụ: Nếu ∠A = ∠A' và ∠B = ∠B' thì ΔABC ~ ΔA'B'C'.
Tỉ số đồng dạng của hai tam giác đồng dạng là tỉ số giữa hai cạnh tương ứng của chúng. Nếu ΔABC ~ ΔA'B'C' thì tỉ số đồng dạng k được tính như sau:
k = AB/A'B' = BC/B'C' = CA/C'A'
Tỉ số đồng dạng có vai trò quan trọng trong việc tính toán các yếu tố của tam giác đồng dạng.
Định nghĩa hai tam giác đồng dạng được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến hình học, đặc biệt là trong việc tính toán độ dài các đoạn thẳng, chiều cao, diện tích của các hình.
Ví dụ:
| Bài toán | Giải pháp |
|---|---|
| Cho ΔABC vuông tại A, có AB = 3cm, AC = 4cm. Gọi D là điểm sao cho ΔABC ~ ΔDBA. Tính độ dài AD. | Vì ΔABC ~ ΔDBA nên AB/DB = BC/BA = AC/DA. Từ đó suy ra DA = AC * BA / BC. Tính BC bằng định lý Pitago: BC = √(AB2 + AC2) = 5cm. Vậy DA = 4 * 3 / 5 = 2.4cm. |
Để củng cố kiến thức về định nghĩa hai tam giác đồng dạng, bạn có thể thực hành với các bài tập sau:
Giaitoan.edu.vn hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về định nghĩa hai tam giác đồng dạng. Chúc bạn học tập tốt!