Bài viết này sẽ hướng dẫn bạn một cách chi tiết về cách tính xác suất của biến cố bằng tỉ số. Đây là một kiến thức cơ bản và quan trọng trong môn Toán học, đặc biệt là trong lĩnh vực xác suất thống kê.
Chúng ta sẽ cùng nhau khám phá định nghĩa, công thức và các ví dụ minh họa để bạn có thể hiểu rõ và áp dụng thành thạo kiến thức này.
Tính xác suất bằng tỉ số như thế nào? Các bước tính xác suất bằng tỉ số là gì?
1. Lý thuyết
- Công thức tính xác suất bằng tỉ số
Giả thiết rằng các kết quả có thể của một hành động hay thực nghiệm là đồng khả năng. Khi đó, xác suất của biến cố E, kí hiệu là P(E), bằng tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể.
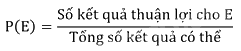
- Các bước tính xác suất bằng tỉ số
Việc tính xác suất của một biến cố E trong một hành động hay thực nghiệm đồng khả năng sẽ gồm các bước sau:
Bước 1. Đếm các kết quả có thể (thường bằng cách liệt kê);
Bước 2. Chỉ ra các kết quả có thể là đồng khả năng;
Bước 3. Đếm các kết quả thuận lợi cho biên cố E;
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể.
- Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản:
+ Xác suất của biến cố trong trò chơi tung đồng xu

Trong trò chơi tung đồng xu, ta có:
- Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt N” bằng \(\frac{1}{2}\).
- Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt S” bằng \(\frac{1}{2}\).
+ Xác suất của biến cố trong trò chơi vòng quay số
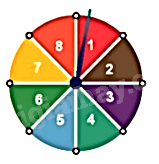
Trong trò chơi vòng quay số đã nêu, nếu k là số kết quả thuận lợi cho một biến cố thì xác suất của biến cố đó bằng \(\frac{k}{8}\).
+ Xác suất của biến cố trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng
Trong trò chơi ngẫu nhiên, một đối tượng từ một nhóm đối tượng, xác suất của một biến cố bằng tỉ số của số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.

2. Ví dụ minh họa
Ví dụ 1. Gieo một con xúc xắc.
Các kết quả có thể của hành động trên là 1, 2, 3, 4, 5, 6 chấm. Có 6 kết quả có thể.
Biến cố E: “Gieo được số chấm lẻ” xảy ra khi gieo được các số lẻ. Do đó các kết quả thuận lợi cho biến cố E là 1, 3, 5. Có 3 kết quả thuận lợi
Xác suất của biến cố E là: \(P(E) = \frac{3}{6} = \frac{1}{2}\).
Ví dụ 2. Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4; 5; 6; 7; 8. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa . Quay đĩa tròn một lần.
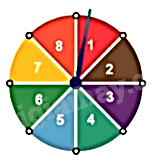
Tính xác suất của các biến cố sau :
a/ “ Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 3”.
b/ “ Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 5”.
c/ “ Mũi tên chỉ vào hình quạt ghi số là ước của 6”.
Lời giải:
a/ Có 2 kết quả thuận lợi cho biến cố “ Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 3” đó là 1;2
Vì thế xác suất của biến cố đó là \(\frac{2}{8} = \frac{1}{4}\) .
b/ Có 4 kết quả thuận lợi cho biến cố “ Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 5” đó là 1;2; 3; 4.
Vì thế xác suất của biến cố đó là \(\frac{4}{8} = \frac{1}{2}\) .
c/ Có 4 kết quả thuận lợi cho biến cố “ Mũi tên chỉ vào hình quạt ghi số là ước của 6” đó là 1;2; 3; 6.
Vì thế xác suất của biến cố đó là \(\frac{4}{8} = \frac{1}{2}\) .
Xác suất là một khái niệm quan trọng trong toán học, đặc biệt là trong lĩnh vực thống kê và lý thuyết xác suất. Nó giúp chúng ta đo lường khả năng xảy ra của một sự kiện hoặc biến cố nào đó. Trong bài viết này, chúng ta sẽ tập trung vào cách tính xác suất của biến cố bằng tỉ số, một phương pháp cơ bản và phổ biến.
Xác suất của một biến cố A, ký hiệu là P(A), là một số thực nằm trong khoảng từ 0 đến 1, biểu thị khả năng xảy ra của biến cố A. P(A) = 0 nghĩa là biến cố A không thể xảy ra, và P(A) = 1 nghĩa là biến cố A chắc chắn xảy ra.
Khi không gian mẫu (tập hợp tất cả các kết quả có thể xảy ra) là hữu hạn và các kết quả là đồng khả năng, xác suất của một biến cố A được tính bằng công thức:
P(A) = (Số kết quả thuận lợi cho A) / (Tổng số kết quả có thể xảy ra)
Ví dụ 1: Gieo một con xúc xắc 6 mặt. Tính xác suất để mặt xuất hiện là số 3.
Ví dụ 2: Rút một lá bài từ bộ bài 52 lá. Tính xác suất để lá bài rút được là lá Át.
a) Bài tập về tung đồng xu: Tính xác suất để tung đồng xu được mặt ngửa hoặc mặt sấp.
b) Bài tập về rút thẻ: Tính xác suất để rút được thẻ có màu đỏ hoặc màu đen từ bộ bài.
c) Bài tập về chọn ngẫu nhiên: Tính xác suất để chọn được một quả bóng màu xanh từ một hộp chứa các quả bóng có màu sắc khác nhau.
Ngoài cách tính xác suất bằng tỉ số, còn có khái niệm về xác suất có điều kiện, là xác suất của một biến cố A xảy ra khi biết rằng một biến cố B đã xảy ra. Công thức tính xác suất có điều kiện là:
P(A|B) = P(A ∩ B) / P(B)
Trong đó:
Xác suất có rất nhiều ứng dụng trong thực tế, bao gồm:
Hãy thử giải các bài tập sau để củng cố kiến thức về cách tính xác suất bằng tỉ số:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về cách tính xác suất của biến cố bằng tỉ số. Chúc bạn học tập tốt!