Hình Chóp Tam Giác Đều

Hình chóp tam giác đều

Hình Chóp Tam Giác Đều: Tổng Quan

Hình chóp tam giác đều là một khái niệm quan trọng trong hình học không gian, thường xuất hiện trong các bài toán thi và kiểm tra. Bài viết này tại giaitoan.edu.vn sẽ cung cấp kiến thức đầy đủ và chi tiết về hình chóp tam giác đều, từ định nghĩa, tính chất đến công thức tính toán và phương pháp giải bài tập.

Chúng ta sẽ cùng nhau khám phá cách xác định các yếu tố của hình chóp, cách tính diện tích xung quanh, diện tích đáy và thể tích của nó. Đồng thời, bài viết cũng sẽ giới thiệu các dạng bài tập thường gặp và hướng dẫn giải chi tiết.

Hình chóp tam giác đều là hình gì?

1. Lý thuyết

- Đặc điểm của hình chóp tam giác đều:

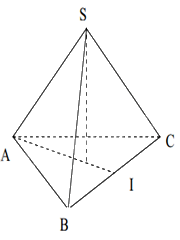
Hình chóp tam giác đều 1

Hình chóp tam giác đều S.ABC có 4 mặt , 6 cạnh.

+ Mặt đáy ABC là một tam giác đều.

+ Các mặt bên SAB, SBC, SCA là những tam giác cân tại S.

+ Các cạnh đáy AB, BC, CA bằng nhau

+ Các cạnh bên SA, SB, SC bằng nhau.

+ S gọi là đỉnh của hình chóp tam giác đều S.ABC.

2. Ví dụ minh họa

Hình ảnh bên là khối Rubik có bốn mặt , các mặt bên, mặt đáy là các tam giác đều.

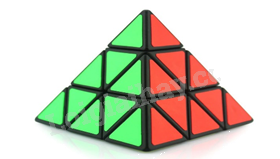
Hình chóp tam giác đều 2

a) Khối Rubik có dạng như hình bên thường được gọi là hình gì ?

b) Cho biết số mặt ,số cạnh ,số đỉnh của hình khối bên ?

c) Hình vẽ bên là hình ảnh một chiếc Rubik – 4 mặt , mỗi mặt đều được ghép bởi những tam giác đều nhỏ bằng nhau. Hãy cho biết có bao nhiêu tam giác đều có trên một mặt của chiếc Rubik này ?

Lời giải

a) Khối Rubik có dạng như hình bên thường được gọi là hình chóp tam giác đều.

b) Số mặt là 4. Số cạnh là 6, số đỉnh là 1.

c) Có 13 tam giác đều có trên một mặt của chiếc Rubik này.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Hình chóp tam giác đều đặc sắc thuộc chuyên mục giải toán 8 trên soạn toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Hình Chóp Tam Giác Đều: Định Nghĩa và Các Khái Niệm Cơ Bản

Hình chóp tam giác đều là hình chóp có đáy là tam giác đều và đỉnh của hình chóp nằm trên đường thẳng vuông góc với tâm của đáy. Các mặt bên của hình chóp tam giác đều là các tam giác cân bằng nhau.

Các Yếu Tố Của Hình Chóp Tam Giác Đều

Đáy: Tam giác đều có cạnh là a.
Đỉnh: Điểm S nằm trên đường thẳng vuông góc với tâm O của đáy.
Chiều cao: Đoạn thẳng SO, ký hiệu là h.
Trung đoạn: Đoạn thẳng nối đỉnh S với trung điểm của một cạnh đáy, ký hiệu là l.
Mặt bên: Các tam giác cân bằng nhau SAB, SBC, SCA.

Tính Chất Quan Trọng Của Hình Chóp Tam Giác Đều

Một số tính chất quan trọng cần lưu ý:

Tất cả các cạnh bên của hình chóp tam giác đều bằng nhau.
Các mặt bên là các tam giác cân bằng nhau.
Đường cao SO đi qua tâm O của đáy.
Trung đoạn l liên hệ với chiều cao h và cạnh đáy a theo công thức: l² = h² + (a√3/6)²

Công Thức Tính Toán

Diện Tích Đáy

Diện tích đáy (S_đáy) của hình chóp tam giác đều được tính theo công thức:

S_đáy = (a²√3)/4

Diện Tích Xung Quanh

Diện tích xung quanh (S_xq) của hình chóp tam giác đều được tính theo công thức:

S_xq = (3/2) * a * l

Diện Tích Toàn Phần

Diện tích toàn phần (S_tp) của hình chóp tam giác đều được tính theo công thức:

S_tp = S_đáy + S_xq = (a²√3)/4 + (3/2) * a * l

Thể Tích

Thể tích (V) của hình chóp tam giác đều được tính theo công thức:

V = (1/3) * S_đáy * h = (1/3) * (a²√3)/4 * h = (a²√3 * h)/12

Các Dạng Bài Tập Thường Gặp và Phương Pháp Giải

Bài Tập Tính Diện Tích và Thể Tích

Đây là dạng bài tập cơ bản nhất, yêu cầu học sinh áp dụng các công thức đã học để tính toán. Cần chú ý đến việc xác định đúng các yếu tố của hình chóp (cạnh đáy, chiều cao, trung đoạn).

Bài Tập Liên Quan Đến Góc

Các bài tập về góc thường yêu cầu tính góc giữa cạnh bên và mặt đáy, góc giữa hai mặt bên, hoặc góc giữa đường cao và cạnh bên. Để giải các bài tập này, cần sử dụng các định lý về góc trong tam giác, góc giữa đường thẳng và mặt phẳng.

Bài Tập Chứng Minh Quan Hệ Hình Học

Dạng bài tập này thường yêu cầu chứng minh một số quan hệ hình học giữa các yếu tố của hình chóp, chẳng hạn như chứng minh một đường thẳng vuông góc với một mặt phẳng, chứng minh hai mặt phẳng vuông góc với nhau.

Ví Dụ Minh Họa

Ví dụ 1: Cho hình chóp tam giác đều S.ABC có cạnh đáy AB = 5cm và chiều cao SO = 4cm. Tính diện tích xung quanh và thể tích của hình chóp.

Giải:

Tính trung đoạn l: l² = h² + (a√3/6)² = 4² + (5√3/6)² ≈ 16 + 1.44 = 17.44 => l ≈ 4.17cm
Tính diện tích xung quanh: S_xq = (3/2) * a * l = (3/2) * 5 * 4.17 ≈ 31.28cm²
Tính thể tích: V = (a²√3 * h)/12 = (5²√3 * 4)/12 ≈ 14.43cm³

Lưu Ý Khi Giải Bài Tập

Luôn vẽ hình chính xác và đầy đủ.
Xác định đúng các yếu tố của hình chóp.
Áp dụng đúng các công thức.
Kiểm tra lại kết quả.

Kết Luận

Hình chóp tam giác đều là một chủ đề quan trọng trong hình học không gian. Việc nắm vững định nghĩa, tính chất, công thức và phương pháp giải bài tập sẽ giúp học sinh giải quyết các bài toán một cách hiệu quả. Hy vọng bài viết này tại giaitoan.edu.vn đã cung cấp cho bạn những kiến thức hữu ích về hình chóp tam giác đều.