Đường phân giác của một góc trong tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề góc đó. Đây là một trong những tính chất quan trọng và thường xuyên được sử dụng trong các bài toán hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài học chi tiết, dễ hiểu về tính chất này, kèm theo các ví dụ minh họa và bài tập thực hành đa dạng để giúp bạn nắm vững kiến thức.
Đường phân giác của tam giác có tính chất gì?
1. Lý thuyết
Tính chất:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Chú ý: Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.
2. Ví dụ minh họa
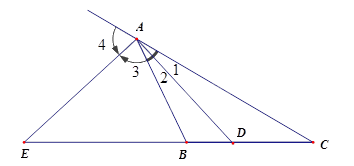
Cho tam giác ABC có $AD,\,AE$ lần lượt là đường phân giác góc trong và góc ngoài tại đỉnh $A$.
Khi đó ta có $\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}$ và $\dfrac{{EB}}{{EC}} = \dfrac{{AB}}{{AC}}$.
Đường phân giác trong tam giác là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học. Nó đóng vai trò then chốt trong việc giải quyết nhiều bài toán liên quan đến tỉ lệ và độ dài đoạn thẳng. Bài viết này sẽ cung cấp một cái nhìn toàn diện về tính chất đường phân giác trong tam giác, bao gồm định nghĩa, các tính chất liên quan, và ứng dụng trong giải toán.
Trong một tam giác, đường phân giác của một góc là đoạn thẳng nối đỉnh của góc đó với điểm chia cạnh đối diện thành hai đoạn thẳng bằng nhau. Điểm chia cạnh đối diện này được gọi là chân đường phân giác.
Tính chất quan trọng nhất của đường phân giác trong tam giác được phát biểu như sau:
Tính chất này cho thấy tỉ lệ giữa hai cạnh kề góc được phân giác bằng tỉ lệ giữa hai đoạn thẳng mà đường phân giác chia cạnh đối diện.
Có nhiều cách để chứng minh tính chất này. Một trong những cách phổ biến nhất là sử dụng định lý Thales và các tam giác đồng dạng.
Chứng minh:
Tính chất đường phân giác có nhiều ứng dụng trong việc giải toán hình học, đặc biệt là các bài toán liên quan đến tỉ lệ đoạn thẳng.
Ví dụ 1: Cho tam giác ABC có AB = 6cm, AC = 9cm, và AD là đường phân giác của góc BAC (D nằm trên BC). Tính độ dài BD và DC.
Giải:
Áp dụng tính chất đường phân giác, ta có: AB/AC = BD/DC => 6/9 = BD/DC => BD/DC = 2/3
Suy ra, BD = (2/3)DC. Mà BD + DC = BC, nên (2/3)DC + DC = BC => (5/3)DC = BC => DC = (3/5)BC
BD = (2/5)BC. Để tính được BD và DC, ta cần biết độ dài BC.
Các bài tập về tính chất đường phân giác thường gặp các dạng sau:
Tính chất đường phân giác trong tam giác là một công cụ hữu ích trong hình học. Việc nắm vững tính chất này và các ứng dụng của nó sẽ giúp bạn giải quyết nhiều bài toán một cách hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.