Hình thoi là một khái niệm quan trọng trong hình học, thường xuất hiện trong các bài toán liên quan đến tính chất đường thẳng, góc và diện tích. Việc nắm vững dấu hiệu nhận biết hình thoi là nền tảng để giải quyết các bài tập một cách chính xác và hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng và tài liệu học tập chi tiết, giúp bạn hiểu rõ về hình thoi và các dấu hiệu nhận biết nó.
Làm thế nào để nhận biết hình thoi?
1. Lý thuyết
Dấu hiệu nhận biết hình thoi:
+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
2. Ví dụ minh họa
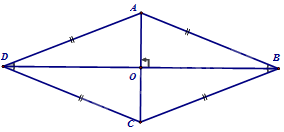
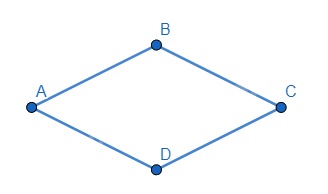
+ Hình bình hành ABCD có AB = BC \( \Leftrightarrow \) ABCD là hình thoi.
+ Hình bình hành ABCD có \(AC \bot BD\) \( \Leftrightarrow \) ABCD là hình thoi.
+ Hình bình hành ABCD có AC là đường phân giác của góc BAD hoặc góc BCD; hoặc BD là đường phân giác của góc ABC hoặc góc ADC \( \Leftrightarrow \) ABCD là hình thoi.
Hình thoi là một tứ giác có bốn cạnh bằng nhau. Tuy nhiên, không phải bất kỳ tứ giác nào có bốn cạnh bằng nhau cũng là hình thoi. Để xác định một tứ giác có phải là hình thoi hay không, chúng ta cần dựa vào các dấu hiệu nhận biết hình thoi. Bài viết này sẽ trình bày chi tiết các dấu hiệu này, kèm theo ví dụ minh họa và bài tập thực hành để giúp bạn hiểu rõ hơn.
Đây là dấu hiệu cơ bản nhất để nhận biết hình thoi. Nếu bạn chứng minh được bốn cạnh của một tứ giác bằng nhau, bạn có thể kết luận đó là hình thoi.
Dấu hiệu này mở rộng từ định nghĩa của hình bình hành. Nếu một tứ giác vừa là hình bình hành vừa có hai cặp cạnh đối bằng nhau, thì nó chắc chắn là hình thoi.
Đây là một dấu hiệu quan trọng và thường được sử dụng trong các bài toán hình học. Nếu bạn chứng minh được hai đường chéo của một tứ giác cắt nhau vuông góc, bạn có thể kết luận đó là hình thoi.
Dấu hiệu này liên quan đến tính chất của đường phân giác trong hình thoi. Nếu một đường chéo của một tứ giác chia góc tại đỉnh đó thành hai góc bằng nhau, thì tứ giác đó là hình thoi.
Dấu hiệu này ít được sử dụng hơn, nhưng vẫn có thể áp dụng trong một số trường hợp cụ thể.
Ví dụ 1: Cho tứ giác ABCD có AB = BC = CD = DA. Chứng minh ABCD là hình thoi.
Giải: Vì ABCD có bốn cạnh bằng nhau (AB = BC = CD = DA) nên theo dấu hiệu 1, ABCD là hình thoi.
Ví dụ 2: Cho tứ giác MNPQ có MN song song với PQ và MQ song song với NP, đồng thời MN = PQ và MQ = NP. Chứng minh MNPQ là hình thoi.
Giải: Vì MNPQ có hai cặp cạnh đối song song và bằng nhau (MN song song với PQ và MN = PQ, MQ song song với NP và MQ = NP) nên theo dấu hiệu 2, MNPQ là hình thoi.
Việc nắm vững các dấu hiệu nhận biết hình thoi có nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng và thiết kế. Ví dụ, trong kiến trúc, hình thoi thường được sử dụng để tạo ra các cấu trúc độc đáo và ấn tượng. Trong xây dựng, hình thoi có thể được sử dụng để tăng cường độ bền của các công trình. Trong thiết kế, hình thoi có thể được sử dụng để tạo ra các sản phẩm thẩm mỹ và hấp dẫn.
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về dấu hiệu nhận biết hình thoi. Việc hiểu rõ các dấu hiệu này sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng nó vào thực tế.