Mặt phẳng tọa độ là một trong những khái niệm cơ bản và quan trọng nhất trong chương trình Hình học lớp 10. Việc nắm vững kiến thức về mặt phẳng tọa độ sẽ giúp bạn giải quyết hiệu quả các bài toán liên quan đến hình học phân tích.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập đa dạng và phương pháp giải bài tập hiệu quả về chủ đề này.
Mặt phẳng tọa độ là gì? Tọa độ của một điểm là gì? Làm thế nào để xác định một điểm trên mặt phẳng tọa độ?
1. Lý thuyết
- Khái niệm Mặt phẳng tọa độ: Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.
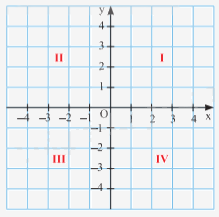
+ Ox nằm ngang gọi là trục hoành;
+ Oy thẳng đứng gọi là trục tung;
+ O gọi là gốc tọa độ.
Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: góc phần tư thứ I, II, III, IV.
- Khái niệm Tọa độ của một điểm:
Trong mặt phẳng tọa độ, mỗi điểm P xác định duy nhất một cặp số (a; b) và mỗi cặp số (a; b) xác định duy nhất một điểm P.
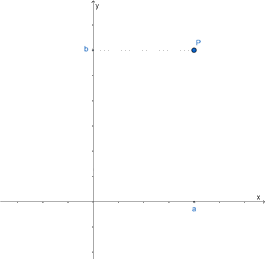
Cặp số (a; b) gọi là tọa độ của P, kí hiệu là M(a; b), trong đó a là hoành độ, b là tung độ của điểm P.
- Cách xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó:
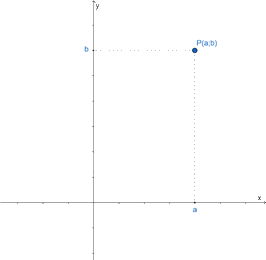
Để xác định một điểm điểm P có tọa độ là (a; b), ta thực hiện các bước sau:
- Tìm trên trục hoành điểm a và vẽ đường thẳng vuông góc với trục này tại điểm a.
- Tìm trên trục tung điểm b và vẽ đường thẳng vuông góc với trục này tại điểm b.
- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm P cần tìm.
Chú ý: Trên mặt phẳng tọa độ, mỗi cặp số (a; b) xác định một điểm P duy nhất.
Nhận xét: Trong mặt phẳng tọa độ, mỗi điểm M xác định một cặp số. Ngược lại, mỗi cặp số xác định một điểm P.
+ Điểm nằm trên trục hoành có tung độ bằng 0.
+ Điểm nằm trên trục tung có hoành độ bằng 0.
2. Ví dụ minh họa
Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.
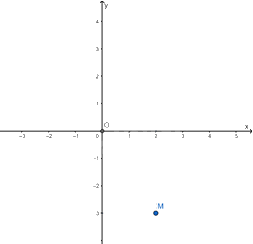
Biểu diễn điểm M(2; -3) trên mặt phẳng tọa độ Oxy
Qua điểm 2 trên trục Ox, kẻ đường thẳng vuông góc với trục Ox.
Qua điểm -3 trên trục Oy, kẻ đường thẳng vuông góc với trục Oy.
Hai đường thẳng trên cắt nhau tại điểm M(2; -3).
Mặt phẳng tọa độ, hay còn gọi là hệ tọa độ Descartes, là một hệ thống dùng để xác định vị trí của các điểm trong mặt phẳng bằng các cặp số thực. Hệ tọa độ bao gồm hai trục vuông góc nhau: trục hoành (trục x) và trục tung (trục y). Giao điểm của hai trục này được gọi là gốc tọa độ (O).
Hệ tọa độ Descartes là hệ tọa độ phổ biến nhất, được sử dụng rộng rãi trong toán học và các lĩnh vực khoa học khác. Mỗi điểm trong mặt phẳng được xác định bằng một cặp số (x, y), gọi là tọa độ của điểm đó. x là hoành độ, y là tung độ.
Tọa độ của một điểm M trong mặt phẳng tọa độ là cặp số (xM, yM), trong đó xM là hoành độ và yM là tung độ của điểm M. Để xác định tọa độ của một điểm, ta thực hiện phép chiếu vuông góc của điểm đó lên trục hoành và trục tung.
Ngoài điểm, trong mặt phẳng tọa độ còn có các yếu tố quan trọng khác như đường thẳng, đoạn thẳng, tia, góc, và vectơ.
Đường thẳng trong mặt phẳng tọa độ được xác định bởi phương trình tổng quát: Ax + By + C = 0, trong đó A, B, C là các hằng số và A, B không đồng thời bằng 0. Có nhiều dạng phương trình đường thẳng khác nhau như phương trình tham số, phương trình chính tắc, phương trình theo đoạn chắn.
Vectơ là một đoạn thẳng có hướng. Vectơ được biểu diễn bằng một cặp số (x, y), trong đó x là hoành độ và y là tung độ của vectơ. Các phép toán trên vectơ như cộng, trừ, nhân với một số thực cũng được thực hiện trên các cặp số này.
Có rất nhiều bài toán liên quan đến mặt phẳng tọa độ, bao gồm:
Mặt phẳng tọa độ có rất nhiều ứng dụng trong thực tế, bao gồm:
Để giải bài tập về mặt phẳng tọa độ hiệu quả, bạn cần:
Bài toán: Tìm tọa độ giao điểm của hai đường thẳng d1: 2x + y = 5 và d2: x - y = 1.
Giải:
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình:
| 2x + y = 5 | (1) |
| x - y = 1 | (2) |
Cộng (1) và (2) vế theo vế, ta được: 3x = 6 => x = 2.
Thay x = 2 vào (2), ta được: 2 - y = 1 => y = 1.
Vậy giao điểm của hai đường thẳng là (2, 1).
Mặt phẳng tọa độ là một công cụ quan trọng trong toán học và các lĩnh vực khoa học khác. Việc nắm vững kiến thức về mặt phẳng tọa độ sẽ giúp bạn giải quyết hiệu quả các bài toán và ứng dụng trong thực tế. Hãy luyện tập thường xuyên và tìm hiểu thêm các tài liệu tham khảo để nâng cao kiến thức của mình.