Trong chương trình hình học không gian, việc tính diện tích xung quanh của hình chóp tam giác đều là một kiến thức quan trọng. Bài viết này tại giaitoan.edu.vn sẽ cung cấp cho bạn công thức, phương pháp và các bài tập minh họa để nắm vững kiến thức này.
Chúng ta sẽ cùng nhau khám phá cách xác định các yếu tố cần thiết và áp dụng công thức một cách hiệu quả.
Công thức tính diện tích xung quanh hình chóp tam giác đều là hình gì?
1. Lý thuyết
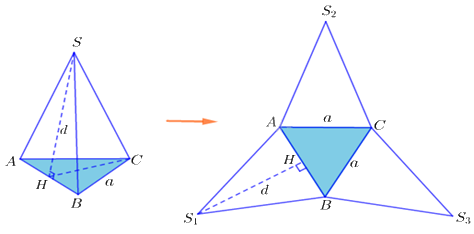
- Diện tích xung quanh của hình chóp tam giác đều bằng nữa tích của chu vi đáy với độ dài trung đoạn.
- Công thức tổng quát : \({S_{xq}} = \frac{1}{2}.C.d\) . Với :
+ \({S_{xq}}\) : Diện tích xung quanh của hình chóp tam giác đều.
+ Chu vi đáy : C = 3.a (a là độ dài cạnh đáy tam giác đều).
+ d: Độ dài trung đoạn của hình chóp tam giác đều.
2. Ví dụ minh họa
Cho hình chóp tam giác đều S.ABC với kích thước như hình vẽ.
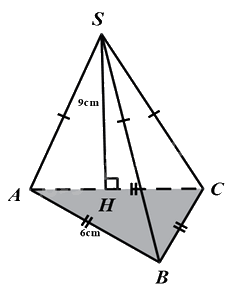
a) Tính chu vi tam giác ABC .
b) Cho biết độ dài trung đoạn hình chóp S.ABC.
c) Tính diện tích xung quanh của hình chóp tam giác đều S.ABC.
Lời giải:
a) Chu vi tam giác ABC là: C = 3a = 3.6 = 18 (cm).
b) Độ dài trung đoạn hình chóp S.ABC là d = SH = 9 (cm)
c) Diện tích xung quanh của hình chóp tam giác đều S.ABC là :
\({S_{xq}} = \frac{1}{2}.C.d = \frac{1}{2}.18.9 = 81(c{m^2})\)
Hình chóp tam giác đều là một hình đa diện có đáy là tam giác đều và các mặt bên là các tam giác cân bằng nhau. Diện tích xung quanh của hình chóp tam giác đều là tổng diện tích của các mặt bên này. Hiểu rõ khái niệm và công thức tính diện tích xung quanh là nền tảng quan trọng để giải quyết các bài toán liên quan đến hình chóp tam giác đều.
Diện tích xung quanh của hình chóp tam giác đều được tính theo công thức sau:
Sxq = (P * l) / 2
Trong đó:
Vì đáy là tam giác đều, nên chu vi đáy được tính bằng công thức:
P = 3 * a
Trong đó:
Chiều cao mặt bên (l) có thể được tính bằng định lý Pitago trong tam giác vuông tạo bởi chiều cao của hình chóp, nửa cạnh đáy và chiều cao mặt bên:
l2 = h2 + (a/2)2
Trong đó:
Từ đó suy ra:
l = √(h2 + (a/2)2)
Cho hình chóp tam giác đều có cạnh đáy a = 5cm và chiều cao h = 4cm. Tính diện tích xung quanh của hình chóp.
1. Một hình chóp tam giác đều có cạnh đáy 6cm và chiều cao 8cm. Tính diện tích xung quanh của hình chóp.
2. Một hình chóp tam giác đều có diện tích xung quanh là 60cm2 và cạnh đáy 5cm. Tính chiều cao của hình chóp.
Diện tích toàn phần của hình chóp tam giác đều được tính bằng tổng diện tích xung quanh và diện tích đáy:
Stp = Sxq + Sđáy
Trong đó:
Kiến thức về diện tích xung quanh của hình chóp tam giác đều có ứng dụng trong nhiều lĩnh vực như kiến trúc, xây dựng, thiết kế đồ họa và các bài toán thực tế khác. Việc nắm vững kiến thức này giúp chúng ta giải quyết các vấn đề một cách hiệu quả và chính xác.
Hy vọng bài viết này tại giaitoan.edu.vn đã cung cấp cho bạn những kiến thức cần thiết về diện tích xung quanh của hình chóp tam giác đều. Hãy luyện tập thêm các bài tập để củng cố kiến thức và áp dụng vào giải quyết các bài toán thực tế.