Hàm số bậc nhất là một trong những khái niệm cơ bản và quan trọng trong chương trình Toán học. Việc hiểu rõ về đồ thị của hàm số bậc nhất giúp học sinh dễ dàng hình dung và giải quyết các bài toán liên quan.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập đa dạng và phương pháp giải bài tập hiệu quả về đồ thị hàm số bậc nhất.
Đồ thị của hàm số bậc nhất có tính chất gì? Vẽ đồ thị hàm số bậc nhất như thế nào?
1. Lý thuyết
- Tính chất của Đồ thị hàm số \(y = ax + b\left( {a \ne 0} \right)\)
Đồ thị hàm số \(y = ax + b\left( {a \ne 0} \right)\) :
+ Là một đường thẳng.
+ Cắt trục tung tại điểm có tung độ bằng b.
- Cách vẽ đồ thị hàm số :
* Trường hợp 1 : Xét hàm số \(y = ax\left( {a \ne 0} \right)\,\left( {b = 0} \right)\):
Để vẽ đồ thị hàm số này ta cót hể xác định điểm A(1;a) rồi vẽ đường thẳng đi qua hai điểm O và A.
* Trường hợp 2 : Xét hàm số \(y = ax + b\left( {a \ne 0} \right)\):
Để vẽ đồ thị hàm số này ta có thể xác định hai điểm P(0;b) và Q\(\left( {\frac{{ - b}}{a};0} \right)\) rồi vẽ đường thẳng đi qua hai điểm đó.
2. Ví dụ minh họa
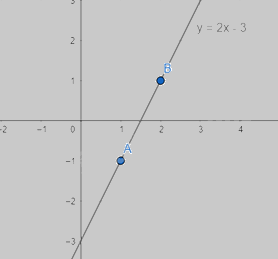
Ví dụ về Đồ thị hàm số: Cho hàm số y = 2x – 3 có hai điểm A(1, -1) và B(2; 1) thuộc đồ thị của hàm số y = 2x – 3.
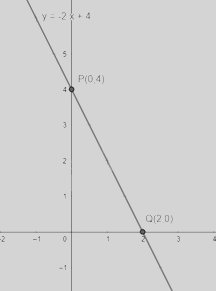
Ví dụ Vẽ đồ thị hàm số: Cho hàm số y = -2x + 4
Với x = 0 thì y = 4, ta được điểm P(0;4)
Với y = 0 thì x = 2, ta được điểm Q(2;0)
Vậy đồ thị hàm số y = -2x + 4 là đường thẳng
Hàm số bậc nhất có dạng tổng quát là y = ax + b, trong đó a và b là các số thực, và a ≠ 0. Đồ thị của hàm số bậc nhất là một đường thẳng.
Để vẽ đồ thị của hàm số bậc nhất y = ax + b, ta cần xác định các yếu tố sau:
Có hai cách phổ biến để vẽ đồ thị hàm số bậc nhất:
Đồ thị của hàm số bậc nhất y = ax + b chính là đường thẳng có phương trình y = ax + b.
Đồ thị hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ:
Bài 1: Vẽ đồ thị của hàm số y = 2x - 1.
Bài 2: Xác định hệ số góc và tung độ gốc của hàm số y = -3x + 2.
Bài 3: Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Khi vẽ đồ thị hàm số bậc nhất, cần chú ý đến hệ số góc a để xác định hướng của đường thẳng. Ngoài ra, cần kiểm tra lại các điểm đã vẽ để đảm bảo tính chính xác của đồ thị.
Việc nắm vững kiến thức về đồ thị hàm số bậc nhất là rất quan trọng đối với học sinh. Hy vọng rằng, với những kiến thức và bài tập được cung cấp trong bài viết này, các bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến chủ đề này.