Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về các tính chất đặc trưng của hình thang cân, giúp bạn nắm vững kiến thức nền tảng.
Học cùng giaitoan.edu.vn, bạn sẽ được trang bị đầy đủ kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Hình thang cân có tính chất gì?
1. Lý thuyết
Tính chất của hình thang cân:
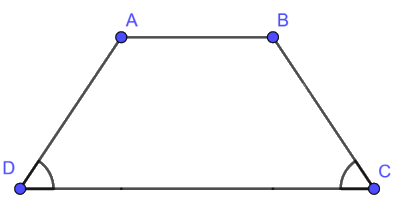
+ Hai cạnh bên bằng nhau.
+ Hai đường chéo bằng nhau.
2. Ví dụ minh họa
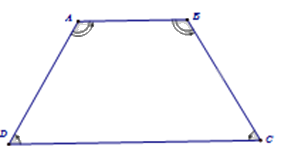
ABCD là hình thang cân thì $AD = BC;\,AC = BD$.
Hình thang cân là một loại hình thang đặc biệt, đóng vai trò quan trọng trong chương trình Hình học lớp 7 và lớp 8. Việc nắm vững các tính chất của hình thang cân không chỉ giúp học sinh giải quyết các bài toán một cách chính xác mà còn là nền tảng cho việc học các kiến thức hình học nâng cao hơn.
Hình thang cân là hình thang có hai cạnh bên song song và hai cạnh bên còn lại bằng nhau. Nói cách khác, một hình thang được gọi là hình thang cân khi nó thỏa mãn đồng thời hai điều kiện sau:
Hình thang cân có những tính chất đặc trưng sau:
Có nhiều cách để chứng minh một hình thang là hình thang cân. Một số phương pháp phổ biến bao gồm:
Các tính chất của hình thang cân được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến hình học, đặc biệt là các bài toán chứng minh, tính toán độ dài cạnh, góc, và diện tích.
Bài tập 1: Cho hình thang cân ABCD với AB // CD, AB = 5cm, CD = 10cm, AD = 6cm. Tính độ dài BC.
Giải: Vì ABCD là hình thang cân nên AD = BC. Do đó, BC = 6cm.
Bài tập 2: Cho hình thang cân ABCD với AB // CD, ∠A = 80°. Tính ∠B, ∠C, ∠D.
Giải: Vì ABCD là hình thang cân nên ∠A = ∠B = 80°. ∠C = ∠D. Vì ∠A + ∠D = 180° nên ∠D = 180° - 80° = 100°. Do đó, ∠C = 100°.
Đường trung bình của hình thang cân là đoạn thẳng nối trung điểm của hai cạnh bên. Đường trung bình của hình thang cân có độ dài bằng trung bình cộng của độ dài hai đáy.
Công thức: m = (AB + CD) / 2
Tính chất của hình thang cân là một kiến thức nền tảng quan trọng trong Hình học. Việc hiểu rõ và nắm vững các tính chất này sẽ giúp bạn tự tin giải quyết các bài toán và tiếp thu các kiến thức hình học nâng cao hơn. Hãy luyện tập thường xuyên và áp dụng các kiến thức đã học vào thực tế để đạt kết quả tốt nhất.