Đoạn thẳng tỉ lệ là một khái niệm quan trọng trong chương trình toán học lớp 7, đặc biệt trong phần hình học.
Hiểu rõ về đoạn thẳng tỉ lệ giúp học sinh giải quyết các bài toán liên quan đến tỉ lệ thức, tính độ dài đoạn thẳng và ứng dụng trong thực tế.
Giaitoan.edu.vn cung cấp các bài giảng và bài tập về đoạn thẳng tỉ lệ được thiết kế khoa học, dễ hiểu, giúp bạn nắm vững kiến thức một cách nhanh chóng.
Tỉ số của hai đoạn thẳng là gì? Đoạn thẳng tỉ lệ là gì?
1. Lý thuyết
- Khái niệm Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Chú ý:
+ Để tính tỉ số của hai đoạn thẳng, ta phải đưa chúng về cùng một đơn vị đo.
+ Tỉ số của hai đoạn thẳng không phụ thuộc vào đơn vị đo độ dài đoạn thẳng.
- Khái niệm Đoạn thẳng tỉ lệ:
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức:
\(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\).
2. Ví dụ minh họa
- Ví dụ về tỉ số của hai đoạn thẳng:
- Ví dụ về đoạn thẳng tỉ lệ:
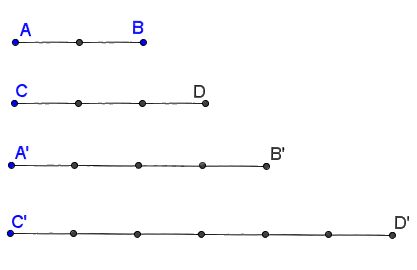
Trong hình dưới đây, ta có \(\frac{{AB}}{{CD}} = \frac{2}{3}\) và \(\frac{{A'B'}}{{C'D'}} = \frac{4}{6} = \frac{2}{3}\). Suy ra \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\).
Trong hình học, đoạn thẳng tỉ lệ là một khái niệm cơ bản nhưng vô cùng quan trọng. Để hiểu rõ về đoạn thẳng tỉ lệ, chúng ta cần nắm vững định nghĩa và các tính chất liên quan.
Hai đoạn thẳng được gọi là tỉ lệ với nhau nếu chúng có cùng tỉ số độ dài. Tức là, nếu đoạn thẳng AB có độ dài là a và đoạn thẳng CD có độ dài là b, thì đoạn thẳng AB và CD tỉ lệ với nhau khi và chỉ khi a/b = k, với k là một hằng số.
a/b = b/c thì a/c.a/b = k thì b/a = 1/k.a/b = c/d = e/f thì (a+c+e)/(b+d+f) = a/b = c/d = e/f.Đoạn thẳng tỉ lệ được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tỉ lệ thức, tam giác đồng dạng, và các bài toán thực tế.
Khi gặp các bài toán về tỉ lệ thức, việc nhận biết và sử dụng tính chất của đoạn thẳng tỉ lệ là vô cùng quan trọng. Ví dụ, để giải bài toán tìm x trong tỉ lệ thức x/5 = 2/10, ta có thể sử dụng tính chất của đoạn thẳng tỉ lệ để tìm ra giá trị của x.
Trong các tam giác đồng dạng, các cạnh tương ứng của chúng tỉ lệ với nhau. Do đó, việc hiểu rõ về đoạn thẳng tỉ lệ giúp chúng ta chứng minh và sử dụng các tính chất của tam giác đồng dạng một cách dễ dàng.
Có rất nhiều dạng bài tập về đoạn thẳng tỉ lệ, bao gồm:
Ví dụ 1: Cho đoạn thẳng AB có độ dài là 8cm và đoạn thẳng CD có độ dài là 12cm. Hãy tính tỉ số của đoạn thẳng AB so với đoạn thẳng CD.
Giải: Tỉ số của đoạn thẳng AB so với đoạn thẳng CD là 8/12 = 2/3.
Ví dụ 2: Cho tam giác ABC có AB = 6cm, BC = 8cm, AC = 10cm. Gọi D là điểm trên AB sao cho AD/DB = 2/3. Tính độ dài đoạn thẳng AD.
Giải: Ta có AD/DB = 2/3, suy ra AD = (2/5) * AB = (2/5) * 6 = 2.4cm.
Để nắm vững kiến thức về đoạn thẳng tỉ lệ, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Đoạn thẳng tỉ lệ là một khái niệm quan trọng trong toán học, đặc biệt trong phần hình học. Việc hiểu rõ về định nghĩa, tính chất và ứng dụng của đoạn thẳng tỉ lệ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin. Hãy luyện tập thường xuyên và sử dụng các tài liệu học tập chất lượng để nắm vững kiến thức này.