Bài viết này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về dấu hiệu nhận biết hình vuông. Chúng ta sẽ cùng nhau khám phá các tính chất đặc trưng giúp phân biệt hình vuông với các hình tứ giác khác.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng mang đến những bài học toán học online dễ hiểu, trực quan và hiệu quả nhất cho học sinh và những người yêu thích môn học này.
Làm thế nào để nhận biết hình vuông?
1. Lý thuyết
Dấu hiệu nhận biết:
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
2. Ví dụ minh họa
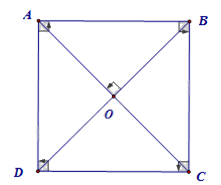
Hình chữ nhật ABCD có AB = BC \( \Leftrightarrow \) ABCD là hình vuông.
Hình chữ nhật ABCD có AC \( \bot \) BD \( \Leftrightarrow \) ABCD là hình vuông.
Hình chữ nhật ABCD có AC là tia phân giác của góc A hoặc hoặc góc C \( \Leftrightarrow \) ABCD là hình vuông.
Hình thoi ABCD có AC = BD \( \Leftrightarrow \) ABCD là hình vuông.
Hình thoi ABCD có \(\widehat A = {90^0};\widehat B = {90^0};\widehat C = {90^0}\) hoặc \(\widehat D = {90^0}\) \( \Leftrightarrow \) ABCD là hình vuông.
Hình vuông là một trong những hình học cơ bản và quan trọng nhất trong chương trình toán học. Việc nắm vững các dấu hiệu nhận biết hình vuông không chỉ giúp học sinh giải quyết các bài toán hình học một cách chính xác mà còn là nền tảng cho việc học các khái niệm toán học nâng cao hơn.
Hình vuông là một tứ giác lồi có bốn cạnh bằng nhau và bốn góc vuông. Điều này có nghĩa là:
Có nhiều dấu hiệu khác nhau để nhận biết một hình vuông. Dưới đây là những dấu hiệu quan trọng nhất:
Nếu một tứ giác có bốn cạnh bằng nhau và một góc vuông thì đó là hình vuông.
Chứng minh: Gọi tứ giác đó là ABCD, với AB = BC = CD = DA và ∠A = 90°. Vì AB = AD và ∠A = 90°, tam giác ABD là tam giác vuông cân, suy ra ∠ABD = ∠ADB = 45°. Tương tự, vì BC = CD và ∠C = 90°, tam giác BCD là tam giác vuông cân, suy ra ∠CBD = ∠CDB = 45°. Do đó, ∠ABC = ∠ABD + ∠CBD = 45° + 45° = 90° và ∠ADC = ∠ADB + ∠CDB = 45° + 45° = 90°. Vậy, tứ giác ABCD có bốn cạnh bằng nhau và bốn góc vuông, nên ABCD là hình vuông.
Nếu một tứ giác có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường thì đó là hình vuông.
Chứng minh: Gọi tứ giác đó là ABCD, với AC = BD, AC ⊥ BD và O là giao điểm của AC và BD sao cho AO = OC = BO = OD. Vì AO = BO và ∠AOB = 90°, tam giác AOB là tam giác vuông cân, suy ra AB = √(AO² + BO²) = √(2AO²). Tương tự, BC = √(BO² + CO²) = √(2BO²) = √(2AO²). Vậy, AB = BC. Lặp lại quá trình này cho các cạnh khác, ta có AB = BC = CD = DA. Do đó, ABCD là hình vuông.
Nếu một tứ giác có một cặp cạnh đối song song và bằng nhau, đồng thời có một đường chéo vuông góc với một cạnh thì đó là hình vuông.
Các dấu hiệu nhận biết hình vuông được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến chứng minh một tứ giác là hình vuông. Việc nắm vững các dấu hiệu này giúp học sinh tiết kiệm thời gian và công sức trong quá trình giải toán.
Bài 1: Cho tứ giác ABCD có AB = BC = CD = DA và ∠B = 90°. Chứng minh rằng ABCD là hình vuông.
Bài 2: Cho tứ giác MNPQ có MN = PQ, MP = NQ và hai đường chéo MP và NQ cắt nhau tại trung điểm O của mỗi đường. Chứng minh rằng MNPQ là hình vuông.
Việc hiểu rõ và vận dụng thành thạo các dấu hiệu nhận biết hình vuông là vô cùng quan trọng trong quá trình học toán. Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn khi giải các bài toán hình học liên quan đến hình vuông. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất!