Bài viết này cung cấp đầy đủ và chi tiết về Tính chất của hình thoi, một kiến thức quan trọng trong chương trình học Toán lớp 6, 7, 8. Chúng tôi sẽ giúp bạn nắm vững lý thuyết, hiểu rõ các định nghĩa và áp dụng vào giải bài tập một cách hiệu quả.
Tại giaitoan.edu.vn, bạn sẽ được học toán online với phương pháp tiếp cận dễ hiểu, trực quan và có nhiều bài tập thực hành để củng cố kiến thức.
Hình thoi có tính chất gì?
1. Lý thuyết
Khái niệm:
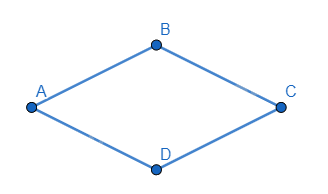
Trong hình thoi:
+ Các cạnh đối song song;
+ Các góc đối bằng nhau;
+ Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;
+ Hai đường chéo là các đường phân giác của các góc ở đỉnh.
+ Hình thoi có đầy đủ tính chất của hình bình hành.
2. Ví dụ minh họa
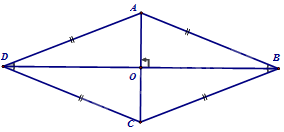
Hình thoi ABCD có:
+ AB // CD; AD // BC
+ \(\widehat A = \widehat C;\widehat B = \widehat D\)
+ \(AC \bot BD;O = AC \cap BD \Rightarrow AO = OC;BO = OD\)
+ AC là đường phân giác của góc DAB và góc DCB; BD là đường phân giác của góc ABC và góc ADC.
Hình thoi là một tứ giác đặc biệt, đóng vai trò quan trọng trong hình học. Để hiểu rõ về hình thoi, chúng ta cần nắm vững các tính chất cơ bản của nó. Bài viết này sẽ đi sâu vào phân tích các tính chất này, cùng với các ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức.
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Có nhiều cách để chứng minh một tứ giác là hình thoi:
Diện tích hình thoi có thể được tính theo nhiều cách:
Bài tập 1: Cho hình thoi ABCD có cạnh AB = 5cm và đường chéo AC = 8cm. Tính độ dài đường chéo BD.
Hướng dẫn: Sử dụng tính chất hai đường chéo vuông góc và cắt nhau tại trung điểm để giải bài toán.
Bài tập 2: Chứng minh rằng nếu một tứ giác có hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường thì tứ giác đó là hình thoi.
Hình thoi xuất hiện trong nhiều ứng dụng thực tế, ví dụ như:
Để hiểu sâu hơn về hình thoi, bạn có thể tìm hiểu thêm về các khái niệm liên quan như hình bình hành, hình chữ nhật, hình vuông. Việc so sánh các hình này sẽ giúp bạn nắm vững hơn các tính chất và ứng dụng của từng hình.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Tính chất của hình thoi. Hãy luyện tập thường xuyên để củng cố kiến thức và áp dụng vào giải các bài tập thực tế. Chúc bạn học tốt!
| Tính chất | Mô tả |
|---|---|
| Cạnh | Bốn cạnh bằng nhau |
| Góc | Các góc đối bằng nhau |
| Đường chéo | Vuông góc và cắt nhau tại trung điểm |
| Bảng tóm tắt các tính chất chính của hình thoi | |