Định lí hai tam giác đồng dạng là một trong những kiến thức cơ bản và quan trọng trong chương trình học Toán lớp 8 và lớp 9. Hiểu rõ định lí này giúp học sinh giải quyết nhiều bài toán liên quan đến hình học, đặc biệt là các bài toán về tam giác.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để giúp bạn nắm vững kiến thức về định lí này.
Định lí hai tam giác đồng dạng là gì?
1. Lý thuyết
Định lí:
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
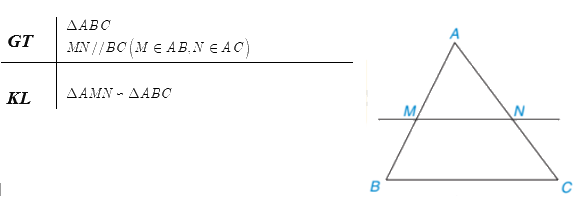
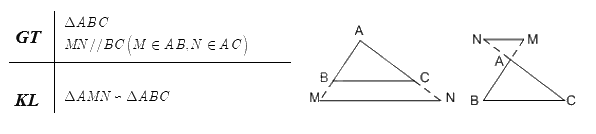
Chú ý: Định lí cũng đúng trong trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại.
2. Ví dụ minh họa
Các đường thẳng AB, CD, EF song song với nhau.
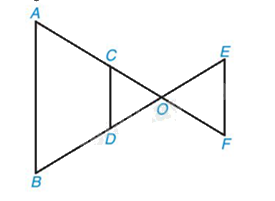
Dựa vào định lí tam giác đồng dạng, ta có:
ΔOCD $\backsim$ ΔOAB (vì CD // AB)
ΔOEF $\backsim$ ΔOCD (vì EF // CD)
ΔOEF $\backsim$ ΔOAB (vì EF // AB)
Định lí hai tam giác đồng dạng là một khái niệm nền tảng trong hình học, đặc biệt quan trọng trong chương trình Toán lớp 8 và lớp 9. Nó mở ra cánh cửa để giải quyết nhiều bài toán phức tạp liên quan đến tam giác và các hình liên quan.
Trước khi đi sâu vào định lí, chúng ta cần hiểu rõ khái niệm tam giác đồng dạng. Hai tam giác được gọi là đồng dạng nếu chúng có:
Khi hai tam giác đồng dạng, ta có thể viết ký hiệu ΔABC ~ ΔA'B'C', trong đó ΔABC và ΔA'B'C' là hai tam giác đồng dạng.
Định lí hai tam giác đồng dạng phát biểu như sau:
Nếu một đường thẳng cắt hai cạnh của một tam giác và tạo ra hai tam giác đồng dạng thì tam giác đó đồng dạng với tam giác còn lại.
Nói cách khác, nếu ΔABC có đường thẳng DE cắt AB tại D và AC tại E sao cho DE // BC, thì ΔADE ~ ΔABC.
Chứng minh định lí dựa trên việc chứng minh hai tam giác ADE và ABC có ba góc bằng nhau:
Vì có ba góc bằng nhau, nên ΔADE ~ ΔABC theo trường hợp góc - góc - góc (AAA).
Từ định lí hai tam giác đồng dạng, ta có những hệ quả quan trọng sau:
Định lí hai tam giác đồng dạng được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến:
Ví dụ 1: Cho tam giác ABC có DE // BC, AD = 2cm, DB = 3cm, AE = 3cm. Tính độ dài EC.
Giải:
Vì DE // BC nên ΔADE ~ ΔABC. Do đó, ta có:
AD/AB = AE/AC
Thay số: 2/(2+3) = 3/(3+EC)
Giải phương trình, ta được EC = 1.5cm.
Ngoài định lí hai tam giác đồng dạng, còn có các trường hợp đồng dạng khác:
Để nắm vững kiến thức về định lí hai tam giác đồng dạng, bạn nên luyện tập thêm nhiều bài tập khác nhau. Hãy tìm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Định lí hai tam giác đồng dạng là một công cụ mạnh mẽ trong hình học, giúp chúng ta giải quyết nhiều bài toán một cách hiệu quả. Việc hiểu rõ định lí và các ứng dụng của nó là rất quan trọng đối với học sinh lớp 8 và lớp 9.