Bài học này sẽ giúp bạn nắm vững định nghĩa, các tính chất cơ bản và ứng dụng của đường trung bình trong tam giác.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập chi tiết, bài tập đa dạng và phương pháp giải dễ hiểu để bạn có thể tự tin chinh phục môn Toán.
Đường trung bình của tam giác có tính chất gì?
1. Lý thuyết
Tính chất:
Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
2. Ví dụ minh họa
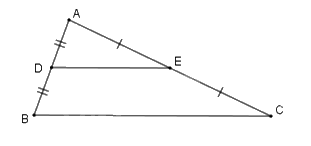
$\Delta ABC$ có $D$ là trung điểm của AB , $E$ là trung điểm của AC nên DE là đường trung bình của tam giác ABC $\Rightarrow DE{\rm{//}}BC;\,DE = \dfrac{1}{2}BC.$
Đường trung bình của tam giác là một khái niệm quan trọng trong hình học, đóng vai trò then chốt trong việc giải quyết nhiều bài toán liên quan đến tam giác. Bài viết này sẽ cung cấp một cái nhìn toàn diện về tính chất đường trung bình của tam giác, bao gồm định nghĩa, các tính chất cơ bản, và ứng dụng thực tế.
Trong một tam giác, đường trung bình là đoạn thẳng nối trung điểm của hai cạnh. Cụ thể, cho tam giác ABC, nếu M là trung điểm của AB và N là trung điểm của AC, thì MN được gọi là đường trung bình của tam giác ABC, ứng với cạnh BC.
Tính chất quan trọng nhất của đường trung bình là nó song song với cạnh thứ ba của tam giác. Trong tam giác ABC, nếu MN là đường trung bình ứng với cạnh BC, thì MN // BC.
Độ dài của đường trung bình bằng một nửa độ dài cạnh thứ ba mà nó song song. Trong tam giác ABC, nếu MN là đường trung bình ứng với cạnh BC, thì MN = 1/2 BC.
Có nhiều cách để chứng minh tính chất đường trung bình. Một trong những cách phổ biến nhất là sử dụng định lý Thales. Giả sử M là trung điểm của AB và N là trung điểm của AC. Khi đó, AM/AB = AN/AC = 1/2. Theo định lý Thales đảo, MN // BC.
Bài 1: Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Biết BC = 10cm. Tính độ dài MN.
Giải: MN là đường trung bình của tam giác ABC ứng với cạnh BC. Do đó, MN = 1/2 BC = 1/2 * 10cm = 5cm.
Bài 2: Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Biết MN // BC. Chứng minh rằng M và N lần lượt là trung điểm của AB và AC.
Giải: Đề bài đã cho MN // BC. Theo định nghĩa đường trung bình, MN là đường thẳng nối trung điểm của hai cạnh AB và AC. Vậy M và N lần lượt là trung điểm của AB và AC.
Khái niệm đường trung bình không chỉ giới hạn trong tam giác. Nó còn được mở rộng trong các hình khác như hình thang. Trong hình thang, đường trung bình là đoạn thẳng nối trung điểm của hai cạnh bên, và có độ dài bằng trung bình cộng độ dài hai đáy.
Tính chất đường trung bình của tam giác là một công cụ hữu ích trong hình học, giúp giải quyết nhiều bài toán một cách nhanh chóng và hiệu quả. Việc nắm vững định nghĩa, các tính chất và ứng dụng của đường trung bình là rất quan trọng để học tốt môn Toán. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về chủ đề này.
| Định nghĩa | Tính chất 1 | Tính chất 2 |
|---|---|---|
| Đoạn thẳng nối trung điểm hai cạnh | Song song với cạnh thứ ba | Bằng một nửa cạnh thứ ba |