Hiểu rõ về tổng các góc của một tứ giác giúp học sinh giải quyết các bài toán liên quan đến tứ giác một cách nhanh chóng và chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập thực hành đa dạng và các phương pháp giải bài tập hiệu quả về chủ đề này.
Tổng các góc của một tứ giác bằng bao nhiêu?
1. Lý thuyết
- Định lý tổng các góc của một tứ giác:
Tổng các góc của một tứ giác bằng \(360^\circ\).
- Dạng toán thường gặp: Tính số đo góc trong tứ giác lồi
Phương pháp giải:
Sử dụng định lí về tổng bốn góc trong một tứ giác bằng \(360^\circ\).
2. Ví dụ minh họa
- Tìm x trong hình sau:
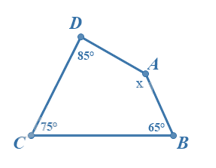
Theo định lí về tổng các góc của một tứ giác, ta có \(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\). Do đó \(\widehat A = x = {360^0} - {85^0} - {75^0} - {65^0} = {135^0}\)
Vậy \(x = {135^0}\)
- Tìm y trong hình sau:
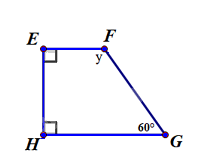
Theo định lí về tổng các góc của một tứ giác, ta có \(\widehat E + \widehat F + \widehat G + \widehat H = {360^0}\). Do đó \(\widehat F = y = {360^0} - {90^0} - {90^0} - {60^0} = {120^0}\)
Vậy \(\widehat F = {120^0}\)
Trong hình học phẳng, tứ giác là một hình đa giác có bốn cạnh và bốn góc. Một trong những tính chất quan trọng nhất của tứ giác là tổng các góc của nó luôn bằng 360 độ. Bài viết này sẽ đi sâu vào khám phá tính chất này, các chứng minh và ứng dụng của nó trong giải toán.
Tứ giác là hình đa giác có bốn cạnh và bốn góc. Các đỉnh của tứ giác là giao điểm của các cạnh kề nhau. Một tứ giác có thể lồi hoặc lõm, tùy thuộc vào vị trí của các góc trong nó.
Tổng các góc của một tứ giác luôn bằng 360 độ. Điều này có thể được biểu diễn bằng công thức:
∠A + ∠B + ∠C + ∠D = 360°
Trong đó:
Có nhiều cách để chứng minh công thức tính tổng các góc của một tứ giác. Một trong những cách phổ biến nhất là chia tứ giác thành hai tam giác bằng cách vẽ một đường chéo.
Giả sử tứ giác ABCD được chia thành hai tam giác ABC và ADC bằng đường chéo AC.
Ta biết rằng tổng các góc của một tam giác là 180 độ. Do đó:
Cộng hai phương trình trên, ta được:
∠BAC + ∠ABC + ∠ACB + ∠DAC + ∠ADC + ∠DCA = 360°
Sắp xếp lại, ta có:
(∠BAC + ∠DAC) + ∠ABC + (∠ACB + ∠DCA) + ∠ADC = 360°
Vì ∠BAC + ∠DAC = ∠BAD và ∠ACB + ∠DCA = ∠BCD, ta có:
∠BAD + ∠ABC + ∠BCD + ∠ADC = 360°
Vậy, tổng các góc của tứ giác ABCD bằng 360 độ.
Công thức tổng các góc của một tứ giác bằng 360 độ áp dụng cho tất cả các loại tứ giác, bao gồm:
Công thức tính tổng các góc của một tứ giác được sử dụng rộng rãi trong giải toán hình học. Dưới đây là một số ứng dụng phổ biến:
Bài toán: Cho tứ giác ABCD có ∠A = 80°, ∠B = 100°, ∠C = 120°. Tính ∠D.
Giải:
Áp dụng công thức tính tổng các góc của một tứ giác, ta có:
∠A + ∠B + ∠C + ∠D = 360°
80° + 100° + 120° + ∠D = 360°
300° + ∠D = 360°
∠D = 360° - 300°
∠D = 60°
Vậy, ∠D = 60°.
Tổng các góc của một tứ giác bằng 360 độ là một tính chất cơ bản và quan trọng trong hình học. Việc nắm vững tính chất này giúp học sinh giải quyết các bài toán liên quan đến tứ giác một cách hiệu quả và chính xác. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về chủ đề này.