Trong chương trình học Toán lớp 8, việc nắm vững các trường hợp đồng dạng của tam giác là vô cùng quan trọng. Trường hợp đồng dạng thứ hai (c.g.c) là một trong những công cụ đắc lực giúp chúng ta chứng minh hai tam giác đồng dạng một cách hiệu quả.
Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ và chi tiết về trường hợp đồng dạng thứ hai, bao gồm định nghĩa, điều kiện áp dụng, ví dụ minh họa và các bài tập luyện tập.
Trường hợp đồng dạng thứ hai là gì?
1. Lý thuyết
Định lí Trường hợp đồng dạng thứ hai (cạnh – góc – cạnh):
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng. 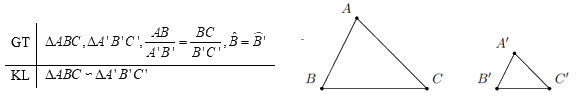
2. Ví dụ minh họa
Ví dụ 1: Cho hình thang ${ABCD}$ (${AB \parallel CD}$). Biết ${AB = 9}$ cm, ${BD = 12}$ cm và ${DC = 16}$ cm. Chứng minh $\Delta ABD\backsim \Delta BDC$.
Lời giải.
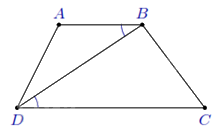
Ta có ${\widehat{ABD}=\widehat{BDC}}$ và ${\frac{BA}{BD}=\frac{DB}{DC}=\frac{3}{4}}$.
\(\Rightarrow \Delta ABD\backsim \Delta BDC\) (c.g.c).
Ví dụ 2: Cho tam giác ${ABC}$ có ${AB = 4}$ cm, ${AC = 8}$ cm. Trên cạnh ${AC}$ lấy ${D}$ sao cho ${AD = 2}$ cm. Chứng minh
a) ${\widehat{ABD} = \widehat{ACB}}$; b) ${BC = 2 BD}$.
Lời giải.
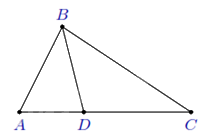
a) Xét $\Delta ABD$ và $\Delta ACB$ có
${\widehat{A}}$ chung, ${\frac{AD}{AB} = \frac{AB}{AC} = \frac{1}{2}}$
$\Rightarrow \Delta ABD\backsim \Delta ACB$ (c.g.c), suy ra ${\widehat{ABD} = \widehat{ACB}}$.
b) Từ câu a), ta có ${\frac{BC}{BD} = \frac{AC}{AB} = 2 \Rightarrow}$ đpcm.
Trường hợp đồng dạng thứ hai của tam giác (c.g.c) phát biểu như sau: Nếu hai tam giác có hai cạnh tương ứng tỉ lệ và góc xen giữa hai cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
Ký hiệu: ΔABC ∽ ΔA'B'C' nếu và chỉ nếu:
Trong đó:
Để chứng minh hai tam giác đồng dạng theo trường hợp c.g.c, ta cần:
Cho tam giác ABC và tam giác A'B'C' có:
Chứng minh ΔABC ∽ ΔA'B'C'.
Giải:
Ta có:
Vậy ΔABC ∽ ΔA'B'C' (c.g.c)
Trường hợp đồng dạng thứ hai (c.g.c) được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác đồng dạng, đặc biệt là trong các bài toán chứng minh hình học và tính toán độ dài đoạn thẳng.
Ví dụ, ta có thể sử dụng trường hợp c.g.c để:
Dưới đây là một số bài tập luyện tập để giúp bạn nắm vững kiến thức về trường hợp đồng dạng thứ hai (c.g.c):
Khi áp dụng trường hợp đồng dạng thứ hai (c.g.c), cần chú ý:
Trường hợp đồng dạng thứ hai (c.g.c) là một công cụ quan trọng trong việc chứng minh hai tam giác đồng dạng. Việc nắm vững định nghĩa, điều kiện áp dụng và các ví dụ minh họa sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả và chính xác.