Trong chương trình học Toán lớp 8, kiến thức về tam giác đồng dạng đóng vai trò vô cùng quan trọng. Đặc biệt, Trường hợp đồng dạng đặc biệt của tam giác vuông là một phần kiến thức cần nắm vững để giải quyết các bài toán hình học một cách hiệu quả.
Bài viết này tại giaitoan.edu.vn sẽ cung cấp cho bạn những kiến thức cơ bản nhất về trường hợp đồng dạng đặc biệt này, cùng với các ví dụ minh họa và bài tập thực hành để bạn có thể hiểu rõ và áp dụng vào giải toán.
Trường hợp đồng dạng đặc biệt của tam giác vuông là gì? Trường hợp cạnh huyền – cạnh góc vuông là gì?
1. Lý thuyết
Trường hợp cạnh huyền – cạnh góc vuông:
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
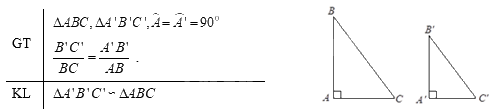
2. Ví dụ minh họa
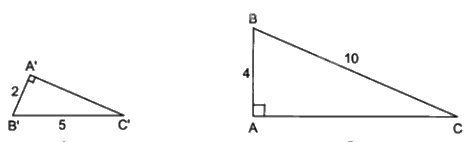
Tam giác A’B’C’ đồng dạng với tam giác ABC vì \(\widehat{A'}=\widehat{A}={{90}^{0}}\); $\frac{A'B'}{AB}=\frac{2}{4}=\frac{1}{2}=\frac{5}{10}=\frac{B'C'}{BC}$.
Trong hình học, hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ. Có ba trường hợp đồng dạng tam giác tổng quát. Tuy nhiên, đối với tam giác vuông, có một trường hợp đồng dạng đặc biệt thường được sử dụng để giải quyết các bài toán liên quan đến tỉ số lượng giác và tính chất của tam giác vuông.
Trường hợp đồng dạng đặc biệt của tam giác vuông phát biểu như sau:
Nếu một tam giác vuông có một góc nhọn bằng góc nhọn của một tam giác vuông khác thì hai tam giác đó đồng dạng.
Điều này có nghĩa là, nếu chúng ta có hai tam giác vuông, ABC và A'B'C', với góc B và B' cùng là góc vuông, và góc A bằng góc A', thì hai tam giác này đồng dạng (ΔABC ~ ΔA'B'C').
Chứng minh trường hợp đồng dạng đặc biệt dựa trên các tính chất sau:
Cụ thể, nếu ΔABC và ΔA'B'C' là hai tam giác vuông với ∠B = ∠B' = 90° và ∠A = ∠A', thì:
∠C = 180° - ∠A - ∠B = 180° - ∠A' - ∠B' = ∠C'.
Do đó, ∠A = ∠A', ∠B = ∠B', và ∠C = ∠C', suy ra ΔABC ~ ΔA'B'C' theo trường hợp góc - góc - góc (AA).
Ví dụ 1: Cho tam giác ABC vuông tại B, biết ∠A = 60°. Cho tam giác A'B'C' vuông tại B', biết ∠A' = 60°. Chứng minh ΔABC ~ ΔA'B'C'.
Giải:
Vì ΔABC và ΔA'B'C' là các tam giác vuông tại B và B' và ∠A = ∠A' = 60°, nên theo trường hợp đồng dạng đặc biệt của tam giác vuông, ta có ΔABC ~ ΔA'B'C'.
Ví dụ 2: Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Cho tam giác A'B'C' vuông tại A', đồng dạng với tam giác ABC và có tỉ lệ đồng dạng k = 2. Tính độ dài các cạnh A'B' và A'C'.
Giải:
Vì ΔA'B'C' ~ ΔABC với tỉ lệ k = 2, ta có:
A'B' = k * AB = 2 * 3cm = 6cm
A'C' = k * AC = 2 * 4cm = 8cm
Trường hợp đồng dạng đặc biệt của tam giác vuông có nhiều ứng dụng trong việc giải các bài toán hình học, đặc biệt là:
Trường hợp đồng dạng đặc biệt của tam giác vuông là một công cụ hữu ích trong việc giải quyết các bài toán hình học. Việc nắm vững lý thuyết và thực hành các bài tập sẽ giúp bạn tự tin hơn trong việc áp dụng kiến thức này vào các bài toán thực tế. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình tại giaitoan.edu.vn.