Hệ số góc của đường thẳng

Hệ số góc của đường thẳng là gì?

Trong chương trình học Toán lớp 10, Hệ số góc của đường thẳng là một khái niệm quan trọng, giúp xác định độ dốc của đường thẳng so với trục hoành. Hiểu rõ về hệ số góc sẽ giúp bạn giải quyết các bài toán liên quan đến phương trình đường thẳng một cách dễ dàng và chính xác.

Tại giaitoan.edu.vn, chúng tôi cung cấp kiến thức đầy đủ, dễ hiểu về hệ số góc, cùng với các bài tập thực hành đa dạng để bạn có thể luyện tập và củng cố kiến thức.

Góc tạo bởi đường thẳng y = ax + b và trục Ox là gì? Hệ số góc là gì?

1. Lý thuyết

- Góc tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục Ox.

Trong mặt phẳng Oxy, cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\). Gọi A là giao điểm của đường thẳng \(y = ax + b\) và trục Ox, T là một điểm thuộc đường thẳng \(y = ax + b\) và có tung độ dương.
Góc \(\alpha \) tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng \(y = ax + b\) và trục Ox ( hoặc nói đường thẳng \(y = ax + b\) tạo với trục Ox một góc \(\alpha \))

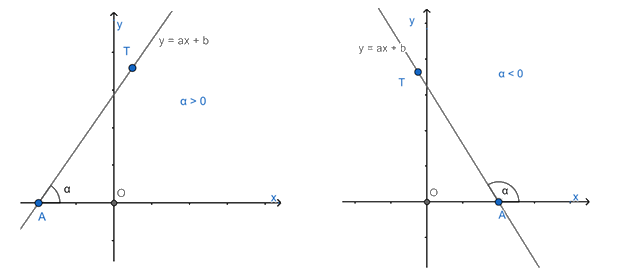
Hệ số góc của đường thẳng 1

- Hệ số góc.

Trên mặt phẳng tọa độ Oxy, cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\). Hệ số a gọi là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\).

2. Ví dụ minh họa

Đường thẳng y = 3x – 1 có hệ số góc là 3;

Đường thẳng y = 2 – x có hệ số góc là -1.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Hệ số góc của đường thẳng đặc sắc thuộc chuyên mục sgk toán 8 trên soạn toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Hệ số góc của đường thẳng: Tổng quan

Hệ số góc của đường thẳng, thường được ký hiệu là k, là một giá trị số thể hiện độ dốc của đường thẳng so với trục hoành. Nó cho biết sự thay đổi của tung độ y khi hoành độ x thay đổi một đơn vị. Hệ số góc đóng vai trò quan trọng trong việc xác định phương trình đường thẳng và phân tích các tính chất hình học của nó.

Công thức tính hệ số góc

Có nhiều cách để tính hệ số góc của đường thẳng, tùy thuộc vào dạng phương trình của đường thẳng:

1. Đường thẳng có phương trình tổng quát: ax + by + c = 0

Hệ số góc của đường thẳng có phương trình tổng quát được tính theo công thức:

k = -a/b (với b ≠ 0)

2. Đường thẳng có phương trình dạng y = mx + b

Trong phương trình này, m chính là hệ số góc của đường thẳng.

3. Đường thẳng đi qua hai điểm A(x₁, y₁) và B(x₂, y₂)

Hệ số góc của đường thẳng đi qua hai điểm A và B được tính theo công thức:

k = (y₂ - y₁) / (x₂ - x₁) (với x₁ ≠ x₂)

Ý nghĩa của hệ số góc

k > 0: Đường thẳng đi lên, tức là khi x tăng thì y cũng tăng.
k < 0: Đường thẳng đi xuống, tức là khi x tăng thì y giảm.
k = 0: Đường thẳng song song với trục hoành.
Đường thẳng thẳng đứng: Hệ số góc không xác định (do mẫu số trong công thức tính bằng 0).

Ứng dụng của hệ số góc

Xác định phương trình đường thẳng: Biết hệ số góc và một điểm thuộc đường thẳng, ta có thể viết phương trình đường thẳng.
Kiểm tra tính song song và vuông góc của hai đường thẳng:
- Hai đường thẳng song song khi và chỉ khi chúng có cùng hệ số góc.
- Hai đường thẳng vuông góc khi và chỉ khi tích hệ số góc của chúng bằng -1.
Giải các bài toán hình học: Hệ số góc được sử dụng để tính góc giữa hai đường thẳng, khoảng cách từ một điểm đến đường thẳng, và các bài toán liên quan đến đường thẳng.

Ví dụ minh họa

Ví dụ 1: Tìm hệ số góc của đường thẳng có phương trình 2x + 3y - 6 = 0.

Giải: Hệ số góc của đường thẳng là k = -2/3.

Ví dụ 2: Đường thẳng đi qua hai điểm A(1, 2) và B(3, 6). Tính hệ số góc của đường thẳng này.

Giải: Hệ số góc của đường thẳng là k = (6 - 2) / (3 - 1) = 4/2 = 2.

Bài tập luyện tập

Để củng cố kiến thức về hệ số góc, bạn có thể thực hành các bài tập sau:

Tìm hệ số góc của các đường thẳng có phương trình sau: y = 5x + 1, x - y + 4 = 0, 3x + 2y = 7.
Xác định hệ số góc của đường thẳng đi qua các cặp điểm sau: (0, 0) và (2, 4), (-1, 3) và (1, -1).
Kiểm tra xem các cặp đường thẳng sau có song song hay vuông góc hay không: y = 2x + 1 và y = 2x - 3, y = -x + 5 và y = x + 2.

Kết luận

Hệ số góc của đường thẳng là một khái niệm cơ bản và quan trọng trong hình học giải tích. Việc nắm vững kiến thức về hệ số góc sẽ giúp bạn giải quyết các bài toán liên quan đến đường thẳng một cách hiệu quả và chính xác. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.